В приложениях робототехники можно использовать множество различных систем координат для определения местоположения роботов, датчиков и других объектов. Как правило, местоположение объекта в 3-D пространстве может определяться значениями положения и ориентации. Для этих значений существует несколько возможных представлений, некоторые из которых специфичны для определенных приложений. Перемещение и вращение являются альтернативными терминами для положения и ориентации. Robotics System Toolbox™ поддерживает представления, которые обычно используются в робототехнике, и позволяет преобразовывать их между ними. При применении этих представлений к 3-D точкам можно выполнять преобразование между системами координат. Эти поддерживаемые представления подробно описаны ниже с краткими пояснениями их использования и числового эквивалента в MATLAB ®. Каждое представление имеет сокращение от своего имени. Используется при присвоении имен аргументам и функциям преобразования, поддерживаемым этой панелью инструментов.
В конце этого раздела вы можете узнать о функциях преобразования, которые мы предлагаем для преобразования между этими представлениями.
Robotics System Toolbox предполагает, что положения и ориентации определяются в правой декартовой системе координат.
Аббревиатура: axang
Поворот в пространстве 3-D описываемый скалярным поворотом вокруг фиксированной оси, определяемой вектором.
Числовое представление: единичный вектор 1 на 3 и скалярный угол, объединенные как вектор 1 на 4
Например, поворот pi/2 радианы вокруг оси y будут:
axang = [0 1 0 pi/2]
Аббревиатура: eul
Эйлеровы углы - это три угла, описывающие ориентацию жёсткого тела. Каждый угол является скалярным поворотом вокруг заданной оси координатной рамки. Панель инструментов системы робототехники поддерживает два порядка поворота. 'ZYZ' порядок осей обычно используется для робототехники. Мы также поддерживаем 'ZYX' порядок осей, который также обозначается как «Шаг крена рыскание (rpy)». Знание используемого порядка осей важно для применения поворота к точкам и при преобразовании в другие представления.
Числовое представление: вектор скалярных углов 1 на 3
Например, поворот вокруг оси y pi будет выражен как:
eul = [0 pi 0]
Примечание.Порядок осей не сохраняется в преобразовании, поэтому необходимо знать, какой порядок поворота должен применяться.
Аббревиатура: tform
Однородная матрица преобразования объединяет перемещение и вращение в одну матрицу.
Числовое представление: матрица 4 на 4
Например, поворот угла α вокруг оси y и перемещение 4 единиц вдоль оси y будет выражаться как:
tform = cos α 0 sin α 0 0 1 0 4 -sin α 0 cos α 0 0 0 0 1
Необходимо предварительно умножить матрицу преобразования на однородные координаты, которые представлены в виде матрицы векторов строк (n на 4 матрицы точек). Использовать транспонирование ('), чтобы повернуть точки для умножения матрицы. Например:
points = rand(100,4); tformPoints = (tform*points')';
Аббревиатура: quat
Кватернион - четырёхэлементный вектор со скалярным вращением и 3-элементный вектор. Кватернионы выгодны тем, что они избегают проблем сингулярности, присущих другим представлениям. Первый элемент, w, является скаляром для нормализации вектора с тремя другими значениями, [x y z] определяющими ось вращения.
Числовое представление: вектор 1 на 4
Например, поворот pi/2 вокруг оси y будет выражаться как:
quat = [0.7071 0 0.7071 0]
Аббревиатура: rotm
Матрица вращения описывает поворот в 3-D пространстве. Является квадратной ортонормированной матрицей с определителем 1.
Числовое представление: матрица 3 на 3
Например, поворот α градусов вокруг оси X будет:
rotm =
1 0 0
0 cos α -sin α
0 sin α cos αНеобходимо предварительно умножить матрицу поворота на координаты, которые представлены в виде матрицы векторов строк (матрица точек n-на-3). Использовать транспонирование ('), чтобы повернуть точки для умножения матрицы. Например:
points = rand(100,3); rotPoints = (rotm*points')';
Аббревиатура: trvec
Вектор перевода представлен в 3D Евклидовом пространстве как Декартовские координаты. Она включает только координатное перемещение, применяемое одинаково ко всем точкам. Ротация отсутствует.
Числовое представление: вектор 1 на 3
Например, перемещение на 3 единицы вдоль оси x и на 2,5 единицы вдоль оси z будет выражено как:
trvec = [3 0 2.5]
Robotics System Toolbox предоставляет функции преобразования для вышеупомянутых представлений преобразования. Не все преобразования поддерживаются выделенной функцией. Ниже приведена таблица, показывающая, какие преобразования поддерживаются (синим цветом). Также показаны сокращения для ротационных и переводных представлений.
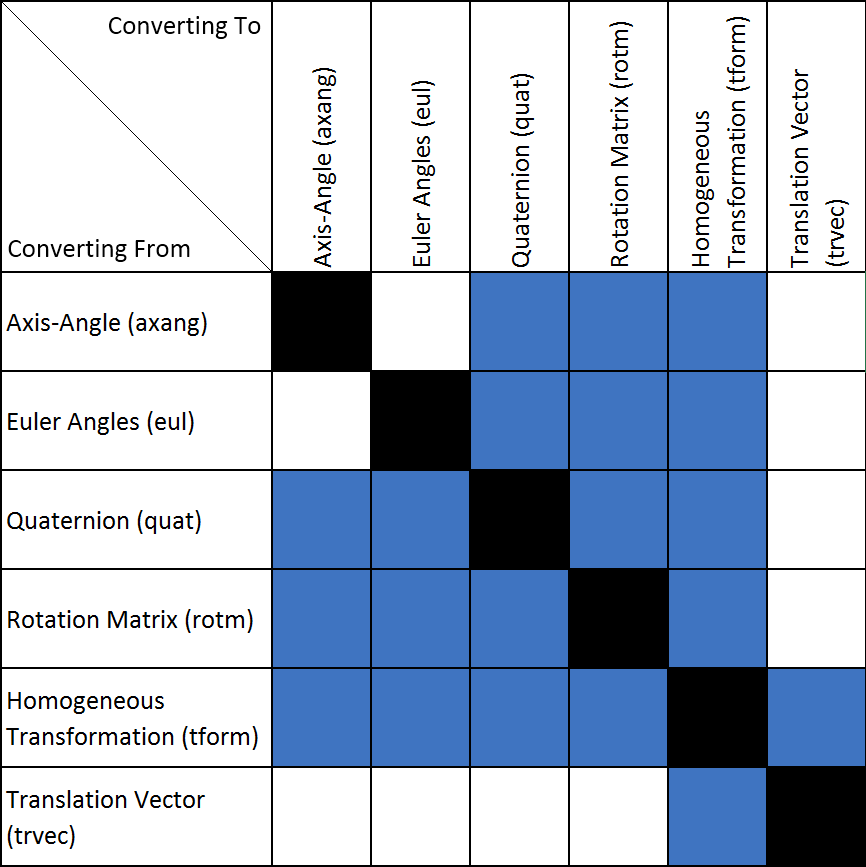
Имена всех функций преобразования соответствуют стандартному формату. Они следуют форме alpha2beta где alpha является аббревиатурой того, что вы преобразуете и beta это то, в что вы преобразуете как аббревиатуру. Например, преобразование углов Эйлера в кватернион будет eul2quat.
Все функции ожидают действительных входных данных. Если указаны недопустимые входные данные, выходные данные не будут определены.
Существуют и другие функции преобразования для преобразования между радианами и градусами, декартовы и однородные координаты, а также для вычисления перепадов углов. Полный список преобразований см. в разделе Преобразования координат и траектории.