Дискретное преобразование Фурье с алгоритмом Гертцеля второго порядка
Оцените частоты тонального сигнала, генерируемого нажатием кнопки 1 на телефонной клавиатуре.
Число 1 выдает тональный сигнал с частотами 697 и 1209 Гц. Создайте 205 выборок тонального сигнала с частотой выборки 8 кГц.
Fs = 8000; N = 205; lo = sin(2*pi*697*(0:N-1)/Fs); hi = sin(2*pi*1209*(0:N-1)/Fs); data = lo + hi;
Используйте алгоритм Гертцеля для вычисления дискретного преобразования Фурье (DFT) тонального сигнала. Выберите индексы, соответствующие частотам, используемым для генерации чисел от 0 до 9.
f = [697 770 852 941 1209 1336 1477]; freq_indices = round(f/Fs*N) + 1; dft_data = goertzel(data,freq_indices);
Постройте график величины ДПФ.
stem(f,abs(dft_data)) ax = gca; ax.XTick = f; xlabel('Frequency (Hz)') ylabel('DFT Magnitude')
Создайте шумный косинус с частотными компонентами на частоте 1,24 кГц, 1,26 кГц и 10 кГц. Укажите частоту дискретизации 32 кГц. Сбросьте генератор случайных чисел для воспроизводимых результатов.
rng default Fs = 32e3; t = 0:1/Fs:2.96; x = cos(2*pi*t*10e3) + cos(2*pi*t*1.24e3) + cos(2*pi*t*1.26e3) ... + randn(size(t));
Создайте частотный вектор. Используйте алгоритм Гертцеля для вычисления DFT. Ограничьте диапазон частот от 1,2 до 1,3 кГц.
N = (length(x)+1)/2; f = (Fs/2)/N*(0:N-1); indxs = find(f>1.2e3 & f<1.3e3); X = goertzel(x,indxs);
Постройте график среднеквадратичного спектра, выраженного в децибелах.
plot(f(indxs)/1e3,mag2db(abs(X)/length(X))) title('Mean Squared Spectrum') xlabel('Frequency (kHz)') ylabel('Power (dB)') grid
Создайте двухканальный сигнал, дискретизированный на частоте 3,2 кГц в течение 10 секунд и встроенный в белый гауссов шум. Первым каналом сигнала является синусоида 124 Гц. Второй канал является комплексным экспоненциальным с частотой 126 Гц. Преобразование сигнала в трехмерную матрицу таким образом, чтобы ось времени проходила вдоль третьего измерения.
fs = 3.2e3; t = 0:1/fs:10-1/fs; x = [cos(2*pi*t*124);exp(2j*pi*t*126)] + randn(2,length(t))/100; x = permute(x,[3 1 2]); size(x)
ans = 1×3
1 2 32000
Вычислите дискретное преобразование Фурье сигнала с помощью алгоритма Гертцеля. Ограничьте диапазон частот от 120 Гц до 130 Гц.
N = (length(x)+1)/2; f = (fs/2)/N*(0:N-1); indxs = find(f>=120 & f<=130); X = goertzel(x,indxs,3);
Постройте график величины дискретного преобразования Фурье, выраженного в децибелах.
plot(f(indxs),mag2db(abs(squeeze(X)))) xlabel('Frequency (Hz)') ylabel('DFT Magnitude (dB)') grid
Алгоритм Гертцеля реализует дискретное преобразование Фурье X (k) как свертку N-точечного входа x (n), n = 0, 1,..., N - 1, с импульсной характеристикой
kn u (n),
где u (n), последовательность единичной стадии, равна 1 для n ≥ 0 и 0 в противном случае. k не обязательно должно быть целым числом. На частоте f = kfs/N, где fs - частота дискретизации, преобразование имеет значение
| n = N,
где
n − m)
и x (N) = 0. Z-преобразование импульсной характеристики
2πkN) z − 1 + z − 2,
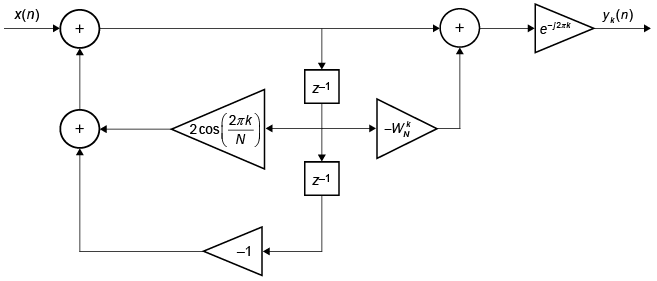
с этой прямой формой II реализации:
Сравнение выходных данных goertzel к результату прямой реализации алгоритма Гертцеля. Для входного сигнала используйте чирп, дискретизированный с частотой 50 Гц в течение 10 секунд и встроенный в белый гауссов шум. Частота чирпа линейно увеличивается от 15 Гц до 20 Гц во время измерения. Вычислить дискретное преобразование Фурье на частоте, которая не является целым кратным fs/N. При звонке goertzelпомните, что векторы MATLAB ® работают от 1 до N, а не от 0 до N-1. Результаты соответствуют высокой точности.
fs = 50; t = 0:1/fs:10-1/fs; N = length(t); xn = chirp(t,15,t(end),20)+randn(1,N)/100; f0 = 17.36; k = N*f0/fs; ykn = filter([1 -exp(-2j*pi*k/N)],[1 -2*cos(2*pi*k/N) 1],[xn 0]); Xk = exp(-2j*pi*k)*ykn(end); dft = goertzel(xn,k+1); df = abs(Xk-dft)
df = 4.3634e-12
Также можно вычислить DFT с помощью:
fft: менее эффективен, чем алгоритм Гертцеля, когда вам нужен только DFT на нескольких частотах. fft является более эффективным, чем goertzel когда нужно оценить преобразование на более чем log2N частотах, где N - длина входного сигнала.
czt: czt вычисляет чирп Z-преобразование входного сигнала на круговом или спиральном контуре и включает ДПФ в качестве специального случая.
[1] Беррус, К. Сидни и Томас В. Паркс. Алгоритмы DFT/FFT и свертки: теория и реализация. Нью-Йорк: John Wiley & Sons, 1985.
[2] Проакис, Джон Г. и Димитрис Г. Манолакис. Цифровая обработка сигналов: принципы, алгоритмы и приложения. 3-е издание. Река Верхнее Седло, Нью-Джерси: Прентис Холл, 1996.
[3] Сысель, Петр и Павел Раджмич. «Алгоритм Гертцеля, обобщенный на немногочисленные кратные фундаментальной частоты». Журнал EURASIP о достижениях в обработке сигналов. Том 2012, номер 1, декабрь 2012, стр. 56-1-56-8. https://doi.org/10.1186/1687-6180-2012-56.