Количество дождевых потоков для анализа усталости
rainflow(___) без выходных аргументов строит график реверсий нагрузки и гистограмму матрицы дождевого потока на текущем рисунке.
Анализ усталости изучает, как происходит накопление повреждений в объекте, подверженном циклическим изменениям напряжения. Количество циклов, необходимых для разрушения объекта, зависит от амплитуды цикла. Широкополосное входное возбуждение содержит циклы различной амплитуды, а наличие гистерезиса в объекте имеет эффект вложенности одних циклов в другие, либо полностью, либо частично. Подсчет дождевого потока оценивает количество циклов изменения нагрузки как функцию амплитуды цикла.
Изначально, rainflow превращает историю нагрузки в последовательность реверсивных операций. Реверсии - это локальные минимумы и максимумы, где знак изменения нагрузки. Функция подсчитывает циклы, рассматривая движущуюся опорную точку последовательности Z и движущееся упорядоченное трехточечное подмножество со следующими характеристиками:
Первая и вторая точки в совокупности называются Y.
Вторая и третья точки в совокупности называются X.
И в X, и в Y точки сортируются от более раннего до более позднего по времени, но не обязательно являются последовательными в последовательности обращения.
Диапазон X, обозначаемый r (X), является абсолютным значением разности между амплитудой первой точки и амплитудой второй точки. Определение r (Y) является аналогичным.
rainflow алгоритм выглядит следующим образом:
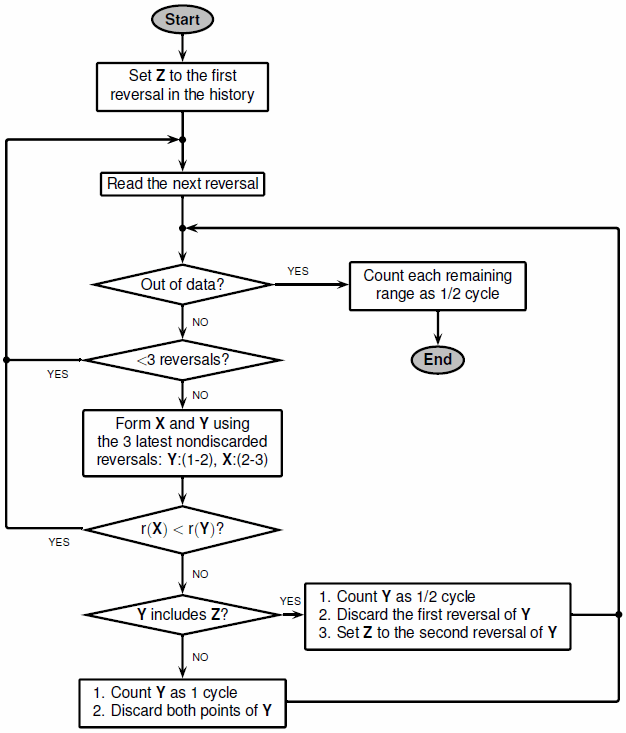
В конце функция собирает различные циклы и полуциклы и суммирует их диапазоны, их средства и точки, в которых они начинаются и заканчиваются. Затем эту информацию можно использовать для получения гистограммы циклов.
Рассмотрим следующую последовательность сторнирования:
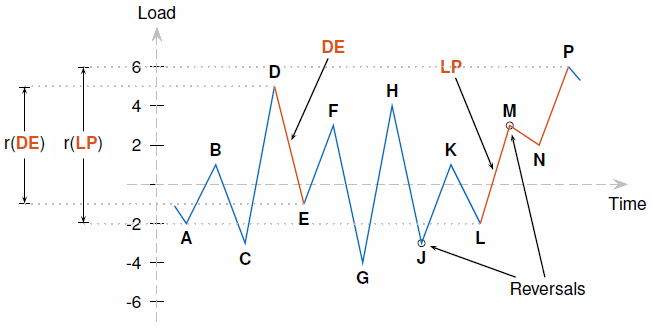
| Шаг | Z | Аннулирования | Три разворота? | Y | r (Y) | X | r (X) | r (X) < r (Y)? | Z в Y? | Действия |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | A, B, C | Да | AB | 3 | До н.э | 4 | Нет | Да |
|
| 2 | B | B, C | Нет | — | — | — | — | — | — | Прочтите Д. |
| 3 | B | B, C, D | Да | До н.э | 4 | CD | 8 | Нет | Да |
|
| 4 | C | C, D | Нет | — | — | — | — | — | — | Прочтите Е. |
| 5 | C | C, D, E | Да | CD | 8 | DE | 6 | Да | — | Читать Ф. |
| 6 | C | C, D, E, F | Да | DE | 6 | EF | 4 | Да | — | Прочтите Г. |
| 7 | C | C, D, E, F, G | Да | EF | 4 | FG | 7 | Нет | Нет |
|
| 8 | C | C, D, G | Да | CD | 8 | DG | 9 | Нет | Да |
|
| 9 | D | D, G | Нет | — | — | — | — | — | — | Прочтите Х. |
| 10 | D | D, G, H | Да | DG | 9 | GH | 8 | Да | — | Читай Дж. |
| 11 | D | D, G, H, J | Да | GH | 8 | HJ | 7 | Да | — | Прочтите К. |
| 12 | D | D, G, H, J, K | Да | HJ | 7 | JK | 4 | Да | — | Читать Л. |
| 13 | D | D, G, H, J, K, L | Да | JK | 4 | KL | 3 | Да | — | Прочтите М. |
| 14 | D | D, G, H, J, K, L, M | Да | KL | 3 | LM | 5 | Нет | Нет |
|
| 15 | D | D, G, H, J, M | Да | HJ | 7 | JM | 5 | Да | — | Читать Н. |
| 16 | D | D, G, H, J, M, N | Да | JM | 5 | MN | 1 | Да | — | Прочтите П. |
| 17 | D | D, G, H, J, M, N, P | Да | MN | 1 | NP | 4 | Нет | Нет |
|
| 18 | D | D, G, H, J, P | Да | HJ | 7 | МИРОВОЙ СУДЬЯ | 9 | Нет | Нет |
|
| 19 | D | D, G, P | Да | DG | 9 | GP | 10 | Нет | Да |
|
| 20 | G | G, P | Недостаточно данных | — | — | — | — | — | — |
Посчитайте GP как ½ цикла. |
Теперь соберите результаты.
| Счетчик циклов | Диапазон | Средний | Начать | Конец |
|---|---|---|---|---|
| ½ | 3 | –0.5 | A | B |
| ½ | 4 | –1 | B | C |
| 1 | 4 | 1 | E | F |
| ½ | 8 | 1 | C | D |
| 1 | 3 | –0.5 | K | L |
| 1 | 1 | 2.5 | M | N |
| 1 | 7 | 0.5 | H | J |
| ½ | 9 | 0.5 | D | G |
| ½ | 10 | 1 | G | P |
Сравните это с результатом выполнения rainflow на последовательности:
q = rainflow([-2 1 -3 5 -1 3 -4 4 -3 1 -2 3 2 6])
q =
0.5000 3.0000 -0.5000 1.0000 2.0000
0.5000 4.0000 -1.0000 2.0000 3.0000
1.0000 4.0000 1.0000 5.0000 6.0000
0.5000 8.0000 1.0000 3.0000 4.0000
1.0000 3.0000 -0.5000 10.0000 11.0000
1.0000 1.0000 2.5000 12.0000 13.0000
1.0000 7.0000 0.5000 8.0000 9.0000
0.5000 9.0000 0.5000 4.0000 7.0000
0.5000 10.0000 1.0000 7.0000 14.0000[1] ASTM E1049-85 (2017), «Стандартная практика подсчета циклов при анализе усталости». Западный Консохокен, Пенсильвания: ASTM International, 2011, https://www.astm.org/cgi-bin/resolver.cgi?E1049.