Документация

Простая модель катализируемых реакций с одной подложкой

Простая модель катализируемых ферментом реакций запускает субстрат S обратимо связываясь с ферментом E. Часть субстрата в комплексе субстрат/фермент превращается в продукт. P с высвобождением фермента.

$$\text{S + E }\underset{\text{k1r}}{\overset{\text{k1}}{\rightleftarrows }}\text{ ES }\stackrel{\text{k2}}{\to }\text{ E + P}$$
$$\text{v1 = k1[S][E], v1r = k1r[ES], v2 = k2[ES]}$$

Эта простая модель может быть определена с помощью

Ферментные реакции с дифференциальными уравнениями скорости

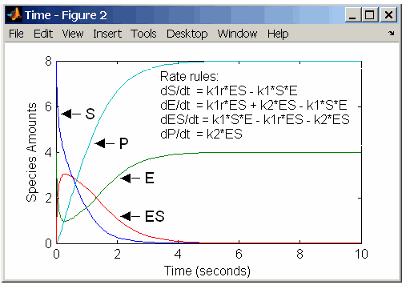
Реакции для механизма реакции фермента с одним субстратом (см. Простую модель катализируемых реакций с одним субстратом) можно описать уравнениями дифференциальной скорости. Можно ввести уравнения дифференциальной скорости в программу в качестве правил скорости.

     reactions: none
 reaction rate: none
    rate rules: dS/dt  = k1r*ES - k1*S*E
                dE/dt  = k1r*ES + k2*ES - k1*S*E
                dES/dt = k1*S*E - k1r*ES - k2*ES
                dP/dt  = k2*ES
       species: S =  8   mole
                E =  4   mole
               ES =  0   mole
                P =  0   mole
    parameters:  k1 = 2   1/(mole*second)
                k1r = 1   1/second
                 k2 = 1.5 1/second

Помните, что правило тарифа dS/dt = f(x) записывается в выражение правила скорости SimBiology ® какS = f(x). Дополнительные сведения о правилах тарифов см. в разделе Правила тарифов.

Кроме того, можно удалить правило ставки для ES, добавить новый вид Etotal для общего количества фермента и добавить алгебраическое правило 0 = Etotal - E - ES, где начальные суммы для Etotal и E равны.

      reactions: none
  reaction rate: none
     rate rules: dS/dt = k1r*ES - k1*S*E
                 dE/dt = k1r*ES + k2*ES - k1*S*E
                 dP/dt = k2*ES
 algebraic rule: 0 = Etotal - E - ES
        species: S =  8   mole
                 E =  4   mole
                ES =  0   mole
                 P =  0   mole
            Etotal =  4   mole
     parameters: k1 = 2   1/(mole*second)
                k1r = 1   1/second
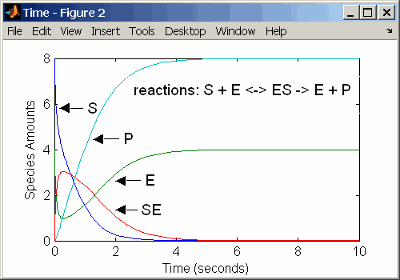
                 k2 = 1.5 1/second

Ферментные реакции с кинетикой массового действия

Определение дифференциальных уравнений скорости для реакций в модели занимает много времени. Лучший способ заключается в том, чтобы вводить реакции для механизма реакции одного субстратного фермента непосредственно в программное обеспечение. Следующий пример с использованием моделей катализируемой ферментом реакции с кинетикой массового действия. Описание модели реакции см. в разделе Простая модель катализируемых реакций с одним субстратом.

     reaction: S + E -> ES
reaction rate: k1*S*E (binding)

     reaction: ES -> S + E 
reaction rate: k1r*ES (unbinding)

     reaction: ES -> E + P
reaction rate: k2*ES (transformation)
      species: S =  8   mole
               E =  4   mole
              ES =  0   mole
               P =  0   mole
   parameters: k1  = 2   1/(mole*second)
               k1r = 1   1/second
               k2  = 1.5 1/second

Результаты моделирования с использованием реакций идентичны результатам использования дифференциальных уравнений скорости.

Ферментные реакции с необратимой кинетикой Анри-Михаэлиса-Ментена

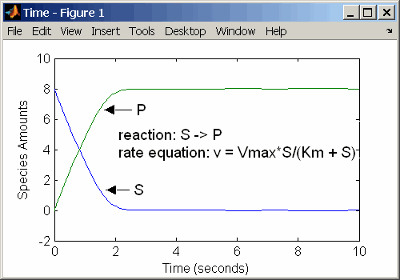
Представление катализируемой ферментом реакции с кинетикой массового действия требует знания констант скорости k1, k1r, и k2. Однако эти константы скорости редко сообщаются в литературе. Чаще дают константы скорости для кинетики Анри-Михаэлиса-Ментена с максимальной скоростью Vm=k2*E и константа Km = (k1r + k2)/k1. Скорость реакции одного субстратного фермента с использованием кинетики Анри-Михаэлиса-Ментена приведена ниже. Сведения о модели см. в разделе Простая модель катализируемых реакций с одной подложкой.

В следующем примере моделируется катализируемая ферментом реакция с использованием кинетики Анри-Михаэлиса-Ментена с одной реакцией и уравнением скорости реакции. Введите в программу реакцию, определенную ниже, и смоделируйте.

     reaction: S -> P
reaction rate: Vmax*S/(Km + S)
      species:    S =  8    mole
                  P =  0    mole
   parameters: Vmax =  6    mole/second
                 Km =  1.25 mole

Результаты показывают, что график немного отличается от графика с использованием кинетики массовых действий. Различия обусловлены допущениями, сделанными при выводе уравнения скорости Михаэлиса-Ментена.