Альберт Гольдбетер модифицировал модель с ферментными каскадами [Goldbeter and Koshland 1981] для соответствия данным клеточного цикла, полученным в исследованиях с эмбриональными клетками [Goldbeter 1991]. Он использовал эту модель для демонстрации порогов с ферментными каскадами и периодическим поведением, вызванным отрицательной обратной связью.
Существует два варианта модели SimBiology ®, использующих модель Гольдбетера. Первая модель использует дифференциальные уравнения скорости непосредственно из статьи Гольдбетера. Вторая модель построена с реакциями с использованием кинетики Анри-Михаэлиса-Ментена .
Альберт Гольдбетер создал простую модель деления клеток из исследований с эмбриональными клетками [Goldbeter 1991]. Эта модель демонстрирует пороги с каскадами ферментов и периодическое поведение, вызванное отрицательной обратной связью.
В модели минимального митотического осциллятора Гольдбетера имеется шесть видов [Goldbeter 1991].
C - Циклин. Периодическое поведение циклина активирует и дезактивирует ферментный каскад.
М +, М - неактивные (фосфорилированные) и активные формы cdc2 киназы. Киназы катализируют добавление фосфатных групп к аминокислотным остаткам.
X +, X - неактивные и активные (фосфорилированные) формы циклин-протеазы. Протеазы разрушают белки, разрывая пептидные связи.
Реакции помечены r1 кому r7 на следующей схеме.
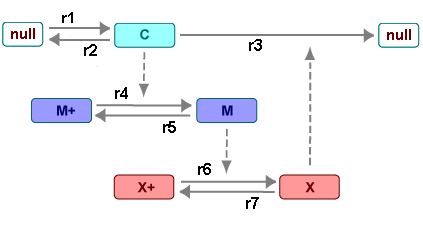
Эта модель показывает:
Как пороги с активацией cdc2 киназы (M + - > M) и активацией протеазы (X + - > X) могут происходить в результате ковалентной модификации (например, фосфорилирования или дефосфорилирования), но без необходимости положительной обратной связи.
Как может происходить периодическое поведение при активации cdc2 киназы с отрицательной обратной связью и временной задержкой, связанной с каскадами активации/дезактивации фермента.
Следующий список описывает каждую из реакций в минимальном митотическом осцилляторе Гольдбетера с некоторыми упрощающими допущениями. Более подробное объяснение модели см. в [Goldbeter 1991].
Циклин (C) синтезируют с постоянной скоростью (r1) и разлагают с постоянной скоростью (r2).
Циклин (C) не образует комплекса с киназой cdc2 (M).
Циклин (C) активирует cdc2 киназу (М + - > М) путем увеличения скорости фосфатазы, которая активирует киназу. Неактивная киназа cdc2 (M+) активируют удалением ингибирующих фосфатных групп (r4).
Количество дезактивирующей киназы (не смоделировано) для cdc2 киназы (M) является постоянной. Активную cdc2 киназу (М) деактивируют добавлением ингибирующей фосфатной группы (r5).
Активация циклин-протеазы (X+ -> X) активной киназой cdc2 (M) является прямым без других промежуточных каскадов. Циклиновая протеаза (X) активируют добавлением фосфатных групп (r6).
Количество дезактивирующей фосфатазы (не смоделированной) для циклиновой протеазы (X) является постоянным. Активная циклиновая протеаза (X) дезактивируют путем удаления активирующих фосфатных групп (r7).
Три интересующих вида - циклин (C), активная дефосфорилированная киназа cdc2 (M) и активная фосфорилированная протеаза (X). Общие суммы (M + M+) и (X + X+) являются постоянными.
Модель минимального митотического осциллятора Гольдбетера определяется тремя дифференциальными уравнениями скорости и двумя алгебраическими уравнениями, которые определяют изменяющиеся параметры в уравнениях скорости.
Уравнение дифференциальной скорости 1, Cyclin (C). Следующее уравнение дифференциальной скорости находится от [Goldbeter 1991] для циклина (C).
C − kdC
Уравнение дифференциальной скорости 2, киназа (М). Следующее дифференциальное уравнение скорости для cdc2 киназы (M). Обратите внимание, что (1 - M) - количество неактивной (фосфорилированной) cdc2 киназы (M+).
M) − V2MK2 + M
+ [C]
Уравнение дифференциальной скорости 3, протеаза (X). Дифференциальные уравнения скорости для циклин-протеазы (X). Обратите внимание, что (1 - X) - количество неактивной (нефосфорилированной) циклиновой протеазы (X+).
X) − V4XK4 + X
[М]
В литературе многие биологические модели определяются с использованием дифференциальной скорости и алгебраических уравнений. С помощью программного обеспечения SimBiology можно вводить уравнения непосредственно как правила SBML. Пример в этом разделе использует митотический осциллятор Гольдбетера для иллюстрации этой точки.
Запись уравнений дифференциальной скорости в однозначном формате, который может понять программа, является довольно простым процессом.
Используйте звездочку для обозначения умножения. Например, k[a] написан k*a.
Снять квадратные скобки, указывающие концентрацию вокруг видов. Единицы, связанные с видом, будут указывать концентрацию (moles/liter) или сумма (moles, molecules).
Программное обеспечение SimBiology использует квадратные скобки вокруг имен видов и параметров, чтобы разрешить имена, которые не являются допустимыми именами переменных MATLAB ®. Например, у вас может быть вид с именемglucose-6-phosphate dehydrogenase но необходимо добавить скобки вокруг имени в уравнениях скорости реакции и правила.
Используйте круглые скобки, чтобы уточнить порядок оценки для математических операций. Например, не пишите ставку Анри-Михаэлиса-Ментена как Vm*C/Kd + C, потому что Vm*C делится на Kd перед добавлением C, а затем C добавляется к результату.
Следующее уравнение является правилом скорости для дифференциального уравнения скорости 1, Cyclin (C):
dC/dt = vi - (vd*X*C)/(Kd + C) - kd*C
Следующие уравнения являются скоростью и repeatedAssignment правила для уравнения дифференциальной скорости 2, киназа (М):
dM/dt = (V1*Mplus)/(K1 + Mplus) - (V2*M)/(K2 + M) V1 = (VM1*C)/(Kc + C) Mplus = Mt - M
Следующие уравнения являются скоростью и repeatedAssignment правила для уравнения дифференциальной скорости 3, протеаза (X):
dX/dt = (V3*Xplus)/(K3 + Xplus) - (V4*X)/(K4 + X) V3 = VM3*M Xplus = Xt - X
Правила. Активный (M) и неактивным (Mplus) формы киназы считаются частью консервативного цикла, при этом общая концентрация (Mt) остается постоянной во время моделирования. Для определения количеств обоих видов требуется только одно дифференциальное уравнение скорости с уравнением баланса масс. Аналогично, активный (X) и неактивным (Xplus) формы протеазы являются частью второго консервативного цикла.
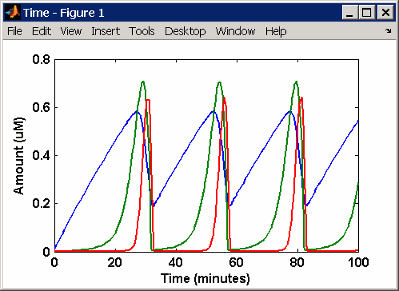
Это моделирование минимального митотического осциллятора Гольдбетера с использованием дифференциальной скорости и алгебраических уравнений. Моделирование с помощью sundials решатель и виды графиков C, M, и X. Описание модели см. в разделе Модель SimBiology с правилами.
В литературе многие модели определены с дифференциальными уравнениями скорости. С помощью программного обеспечения SimBiology создание дифференциальных уравнений из реакций является ненужным; можно ввести реакции и позволить программному обеспечению вычислить уравнения.
Некоторые модели определяются уравнениями дифференциальной скорости, и может потребоваться, чтобы реакции были совместимы с моделью. Для преобразования дифференциальных уравнений скорости в реакции можно использовать два правила:
Для положительного термина - Виды, описанные уравнением, помещаются справа как продукт, а виды в термине помещаются слева как реагенты.
Для отрицательного термина - Виды, описанные уравнением, помещаются слева как продукт, а виды в термине также помещаются слева как реагенты.
Необходимо определить продукты, используя дополнительную информацию, например, схему реакции, описание модели или понимание реакции. Если реакция катализируется киназой, то можно сделать вывод, что продукт имеет одну или несколько дополнительных фосфатных групп.
Простая реакция первого порядка имеет дифференциальное уравнение скорости dR/dt = +kr[P] - kf[R]. Отрицательный термин подразумевает, что реакция R -> ? с неизвестным продуктом. Положительный термин идентифицирует продукт и завершает реакцию, R <-> P.
Реакции, R1 на R3 из уравнения E1. Уравнение 1 дифференциальной скорости повторяется здесь для сравнения с реакциями. См. уравнение дифференциальной скорости 1, Cyclin (C).
Уравнения скорости реакции и скорости реакции из уравнения дифференциальной скорости E1 приведены ниже:
r1 reaction: null -> C reaction rate: vi r2 reaction: C -> null reaction rate: kd*C r3 reaction: C -> null reaction rate: (vd*X*C)/(Kd + C)
Реакции R4 и R5 из уравнения E2. Дифференциальное уравнение скорости 2 и алгебраическое уравнение 2 повторяются здесь для сравнения с реакциями. См. уравнение дифференциальной скорости 2, киназа (М).
M) − V2MK2 + M
+ [C]
Уравнения скорости реакции и скорости реакции из уравнения дифференциальной скорости E2 приведены ниже:
r4 reaction: Mplus -> M
reaction rate: V1*Mplus/(K1 + Mplus)
repeatedAssignment rule: V1 = VM1*C/(Kc + C)
r5 reaction: M -> Mplus
reaction rate: V2*M/(K2 + M)Реакции R6 и R7 из уравнения E3. Дифференциальное уравнение скорости для уравнения 3 и алгебраического уравнения 3 повторяется здесь для сравнения с реакциями.
X) − V4XK4 + X
V3 = VM3*[M]
Уравнения скорости реакции и скорости реакции из уравнения дифференциальной скорости E3 приведены ниже:
r6 reaction: Xplus -> X
reaction rate: V3*Xplus]/(K3 + Xplus)
repeatedAssignment rule: V3 = VM3*M
r7 reaction: X -> Xplus
reaction rate: V4*X/(K4 + X)После преобразования дифференциальных уравнений скорости в реакционные и реакционные уравнения скорости можно приступить к заполнению начальных значений для видов (реагентов и продуктов) и параметров.
Исходные значения параметров и количества для видов перечислены с четырьмя различными единицами измерения в одном измерении:
A - Оригинальные единицы в работе Goldbeter 1991.
B - Единицы концентрации со временем, преобразованным в секунду. При преобразовании a в b используйте 1 minute = 60 second для параметров.
C - Единицы количества в молях. При преобразовании концентрации в моли используйте объем клеток 1e-12 литр и предположим, что объем не меняется.
молесекунда
D - Единицы количества в виде молекул. При преобразовании количества в виде молей в молекулы используйте 6.022e23 molecules = 1 mole.
При включенном анализе размеров и выключенном преобразовании единиц измерения выберите все единицы измерения для одной буквы. Например, выберите все опции Как (As). Если размерный анализ и преобразование единиц включены, можно смешивать и сопоставлять буквы и получать один и тот же ответ.
Реакция 1 Синтез циклина
| R1 | Стоимость | Единицы | |
|---|---|---|---|
| реакция | null - > C | ---- | ---- |
| скорость реакции | vi | ---- | A. uM/минута |
| ---- | B. моль/( литр * секунда) | ||
| ---- | C. Моль/сек. | ||
| ---- | D. Молекула в секунду | ||
| параметры | vi | 0.025 | A. uM/минута |
| 4.167e-10 | B. моль/( литр * секунда) | ||
| 4.167e-22 | C. Моль/сек. | ||
| 205 | D. Молекула в секунду | ||
| разновидности | C | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула |
Реакция 2. Недифференцированная деградация циклина
| R2 | Стоимость | Единицы | |
|---|---|---|---|
| реакция | C -> null | ---- | ---- |
| скорость реакции | kd*C | ---- | A. uM/минута |
| ---- | B. моль/( литр * секунда) | ||
| ---- | C. Моль/сек. | ||
| ---- | D. Молекула в секунду | ||
| параметры | kd | 0.010 | A. 1/минута |
| 1.6667e-4 | B, C, D. 1/сек. | ||
| разновидности | C | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула |
Реакция 3 Разложение циклин-протеазы
| R3 | Стоимость | Единицы | |
|---|---|---|---|
| реакция | C -> null | ---- | ---- |
| скорость реакции | (vd*X*C)/(Kd + C) | ---- | A. uM/минута |
| ---- | B. моль/( литр * секунда) | ||
| ---- | C. Моль/сек. | ||
| ---- | D. Молекула в секунду | ||
| параметр | vd | 0.25 | A. 1/минута |
| 0.0042 | B, C, D. 1/сек. | ||
| параметр | Kd | 0.02 | А. uM |
| 2.0e-8 | B. Моль/литр | ||
| 2.0e-020 | C. Моль | ||
| 12044 | D. Молекула | ||
| разновидности | C (подложка) | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула | ||
| разновидности | X (фермент) | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула |
Реакция 4 Cdc2 Активация киназы
| R4 | Стоимость | Единицы | |
|---|---|---|---|
| реакция | Mplus -> M | ---- | ---- |
| скорость реакции | (V1*Mplus)/(K1 + Mplus) | ---- | A. uM/минута |
| ---- | B. моль/( литр * секунда) | ||
| ---- | C. Моль/сек. | ||
| ---- | D. Молекула в секунду | ||
repeatedAssignment правило | V1 = (VM1*C)/(Kc + C) | ---- | |
| параметр | V1 (переменная по правилу) | 0.00 | A. uM/минута B. моль/( литр * секунда) C. Моль/сек. D. Молекула в секунду |
| параметр | VM1 | 3.0 | A. uM/минута |
| 5.0e-8 | B. моль/( литр * секунда) | ||
| 5.0000e-020 | C. Моль/сек. | ||
| 30110 | D. Молекула в секунду | ||
| параметр | Kc | 0.5 | А. uM |
| 5.0000e-7 | B. Моль/литр | ||
| 5.0e-19 | C. Моль | ||
| 3.011e+5 | D. Молекула | ||
| параметр | K1 | 0.005 | А. uM |
| 5e-9 | B. Моль/литр | ||
| 5e-21 | C. Моль | ||
| 3.011e+3 | D. Молекула | ||
| разновидности | Mplus (неактивная подложка) | 0.99 | А. uM |
| 9.9e-7 | B. Моль/литр | ||
| 9.9e-19 | C. Моль | ||
| 5.962e+5 | D. Молекула | ||
| разновидности | M (активный продукт) | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула | ||
| разновидности | C | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула |
Реакция 5 Cdc2 деактивация киназы
| R5 | Стоимость | Единицы | |
|---|---|---|---|
| реакция | M -> M_plus | ---- | ---- |
| скорость реакции | (V2*M)/(K2 + M) | ---- | A. uM/минута |
| ---- | B. (моль/литр-секунда) | ||
| ---- | C. Моль/сек. | ||
| ---- | D. Молекула в секунду | ||
| параметр | V2 | 1.5 | A. uM/минута |
| 2.5000e-008 | B. Моль/литр-секунда | ||
| 2.5000e-020 | C. Моль/сек. | ||
| 15055 | D. Молекула в секунду | ||
| параметр | K2 | 0.005 | А. uM |
| 5.0000e-009 | B. Моль/литр | ||
| 5.0000e-021 | C. Моль | ||
| 3011 | D. Молекула | ||
| 1.0e-20 | C. Моль | ||
| разновидности | Mplus (неактивно) | 0.99 | А. uM |
| 9.9e-7 | B. Моль/литр | ||
| 9.9e-19 | C. Моль | ||
| 5.962e+5 | D. Молекула | ||
| разновидности | M (активный) | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула |
Реакция 6 Активация протеазы
| R6 | Стоимость | Единицы | |
|---|---|---|---|
| реакция | Xplus -> X | ---- | ---- |
| скорость реакции | (V3*Xplus)/(K3 + Xplus) | ---- | A. uM/минута |
| ---- | B. моль/( литр * секунда) | ||
| ---- | C. Моль/сек. | ||
| ---- | D. Молекула в секунду | ||
repeatedAssignment правило | V3 = VM3*M | ---- | |
| параметр | V3 (переменная по правилу) | A. uM/минута B. Моль/литр-секунда C. Моль/сек. D. Молекула в секунду | |
| параметр | VM3 | 1.0 | A. 1/минута |
| 0.0167 | B, C, D. 1/сек. | ||
| параметр | K3 | 0.005 | А. uM |
| 5e-9 | B. Моль/литр | ||
| 5e-21 | C. Моль | ||
| 3.011e+3 | D. Молекула | ||
| разновидности | Xplus (неактивная подложка) | 0.99 | А. uM |
| 9.9e-7 | B. Моль/литр | ||
| 9.9e-19 | C. Моль | ||
| 5.962e+5 | D. Молекула | ||
| разновидности | X (активный продукт) | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула | ||
| разновидности | M (фермент) | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула |
Реакция 7 Дезактивация протеазы
| R7 | Стоимость | Единицы | |
|---|---|---|---|
| реакция | X -> X_plus | ---- | ---- |
| скорость реакции | (V4*X)/(K4 + X) | ---- | A. uM/минута |
| ---- | B. моль/( литр * секунда) | ||
| ---- | C. Моль/сек. | ||
| ---- | D. Молекула в секунду | ||
| параметр | V4 | 0.5 | A. uM/минута |
| 8.3333e-009 | B. моль/( литр * секунда) | ||
| 8.3333e-021 | C. Моль/сек. | ||
| 5.0183e+003 | D. Молекула в секунду | ||
| параметр | K4 | 0.005 | А. uM |
| 5e-9 | B. Моль/литр | ||
| 5e-21 | C. Моль | ||
| 3011 | D. Молекула | ||
| разновидности | Xplus (неактивно) | 0.99 | А. uM |
| 9.9e-7 | B. Моль/литр | ||
| 9.9e-19 | C. Моль | ||
| 5.962e+5 | D. Молекула | ||
| разновидности | X (активный) | 0.01 | А. uM |
| 1e-8 | B. Моль/литр | ||
| 1.0e-20 | C. Моль | ||
| 6.022e+3 | D. Молекула |
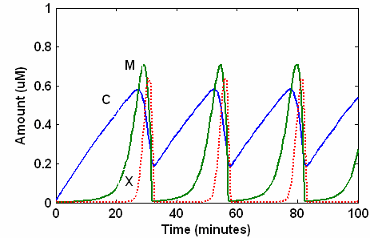
Это симуляция минимального митотического осциллятора Гольдбетера со скоростными и алгебраическими уравнениями. Моделирование с помощью sundials решатель и виды графиков C, M, и X. Описание модели см. в разделе Модель SimBiology с реакциями.
[1] Goldbeter A. (1991), «Минимальная каскадная модель для митотического осциллятора, включающего циклин и cdc2 киназу», Proceedings of the National Academy of Sciences USA, 88: 9107-9111.
[2] Голдбетер А., Кошланд Д. (1981), «Усиленная чувствительность, возникающая в результате ковалентной модификации в биологических системах», Труды Национальной академии наук США, 78: 6840-6844.
[3] Гольдбетер А., Кошланд Д. (1984), «Ультрачувствительность в биохимических системах, контролируемых ковалентной модификацией», The Journal of Biological Chemistry, 259: 14441-14447.
[4] Гольдбетер А., главная страница в Интернете, http://www.ulb.ac.be/sciences/utc/GOLDBETER/agoldbet.html.
[5] Murray A.W., Kirschner M.W. (1989), «Синтез циклина управляет ранним эмбриональным клеточным циклом», Nature, 339: 275-280.