Класс: ClassificationDiscriminant
Ошибка классификации в результате повторного предоставления
L = resubLoss(obj)
L = resubLoss(obj,Name,Value)
L = resubLoss(obj)fitcdiscr используется для создания obj.
L = resubLoss(obj,Name,Value)Name,Value аргументы пары.
|
Ошибка классификации, скаляр. Значение ошибки зависит от значений в |
Вычислите повторно замещенную ошибку классификации для данных радужки Фишера:
load fisheriris
obj = fitcdiscr(meas,species);
L = resubLoss(obj)
L =
0.0200Функции потери классификации измеряют прогностическую неточность классификационных моделей. При сравнении одного и того же типа потерь между многими моделями меньшие потери указывают на лучшую прогностическую модель.
Рассмотрим следующий сценарий.
L - средневзвешенная потеря классификации.
n - размер выборки.
Для двоичной классификации:
yj - наблюдаемая метка класса. Программное обеспечение кодирует его как -1 или 1, указывая отрицательный или положительный класс (или первый или второй класс в ClassNames свойство), соответственно.
f (Xj) - показатель классификации положительного класса для наблюдения (строки) j данных прогнозирования X.
mj = yjf (Xj) - показатель классификации для классификации наблюдения j в класс, соответствующий yj. Положительные значения mj указывают на правильную классификацию и не вносят большого вклада в средние потери. Отрицательные значения mj указывают на неправильную классификацию и вносят значительный вклад в средний убыток.
Для алгоритмов, поддерживающих мультиклассовую классификацию (то есть K ≥ 3):
yj * - вектор из K - 1 нулей, с 1 в положении, соответствующем истинному наблюдаемому классу yj. Например, если истинным классом второго наблюдения является третий класс и K = 4, то y2 * = [0 0 1 0] ′. Порядок классов соответствует порядку в ClassNames свойства входной модели.
f (Xj) - вектор длины K оценок класса для наблюдения j данных предсказателя X. Порядок оценок соответствует порядку классов в ClassNames свойства входной модели.
mj = yj * ′ f (Xj). Поэтому mj - это скалярная оценка классификации, которую модель прогнозирует для истинного наблюдаемого класса.
Вес для наблюдения j равен wj. Программное обеспечение нормализует весовые коэффициенты наблюдения таким образом, что они суммируются с соответствующей вероятностью предыдущего класса. Программное обеспечение также нормализует предыдущие вероятности, так что они составляют 1. Поэтому
С учетом этого сценария в следующей таблице описаны поддерживаемые функции потерь, которые можно указать с помощью 'LossFun' аргумент пары имя-значение.
| Функция потерь | Значение LossFun | Уравнение |
|---|---|---|
| Биномиальное отклонение | 'binodeviance' | |
| Неверно классифицированная скорость в десятичной | 'classiferror' | j - метка класса, соответствующая классу с максимальным баллом. I {·} - функция индикатора. |
| Потери перекрестной энтропии | 'crossentropy' |
Взвешенная потеря перекрестной энтропии равна Kn, где веса нормализуются для суммирования в n вместо 1. |
| Экспоненциальные потери | 'exponential' | ). |
| Потеря шарнира | 'hinge' | |
| Потеря журнала | 'logit' | mj)). |
| Минимальная ожидаемая стоимость классификации ошибок | 'mincost' |
Программное обеспечение вычисляет взвешенную минимальную ожидаемую стоимость классификации, используя эту процедуру для наблюдений j = 1,..., n.
Средневзвешенное минимальное ожидаемое снижение затрат на неправильную классификацию Если используется матрица затрат по умолчанию (значение элемента которой равно 0 для правильной классификации и 1 для неправильной классификации), то |
| Квадратичные потери | 'quadratic' | ) 2. |
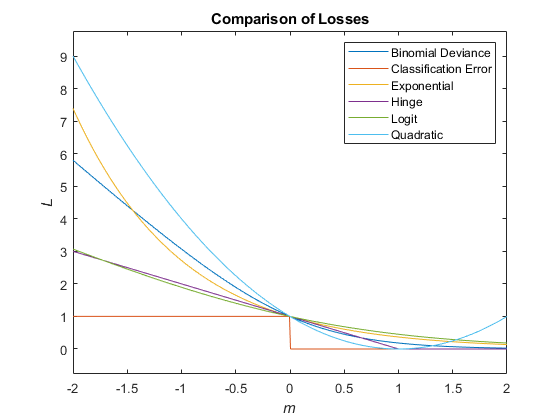
На этом рисунке сравниваются функции потерь (за исключением 'crossentropy' и 'mincost') над баллом м для одного наблюдения. Некоторые функции нормализуются для прохождения через точку (0,1).
