Exponenta Banner
exponenta event banner

fitrgp

Подгонка модели регрессии гауссова процесса (GPR)

свернуть все на странице

Синтаксис

gprMdl = fitrgp (Tbl, ResponseVarName)
gprMdl = fitrgp (Tbl, формула)
gprMdl = fitrgp (Tbl, y)
gprMdl = fitrgp (X, y)
gprMdl = fitrgp (___, имя, значение)

Описание

пример

gprMdl = fitrgp(Tbl,ResponseVarName) возвращает модель регрессии гауссова процесса (GPR), обученную с использованием данных выборки в Tbl, где ResponseVarName - имя переменной ответа в Tbl.

gprMdl = fitrgp(Tbl,formula) возвращает модель регрессии гауссова процесса (GPR), обученную с использованием данных выборки в Tbl, для переменных предиктора и переменных ответа, определенных formula.

gprMdl = fitrgp(Tbl,y) возвращает модель GPR для предикторов в таблице Tbl и вектор непрерывного ответа y.

пример

gprMdl = fitrgp(X,y) возвращает модель GPR для предикторов X и вектор непрерывного ответа y.

пример

gprMdl = fitrgp(___,Name,Value) возвращает модель GPR для любого из входных аргументов в предыдущих синтаксисах с дополнительными опциями, заданными одним или несколькими Name,Value аргументы пары.

Например, можно указать метод аппроксимации, метод прогнозирования, функцию ковариации или метод выбора активного набора. Можно также обучить модель с перекрестной проверкой.

gprMdl является RegressionGP объект. Методы и свойства этого класса см. в разделе RegressionGP страница класса.

Если вы обучаете перекрестно проверенную модель, то gprMdl является RegressionPartitionedModel объект. Для дальнейшего анализа объекта с перекрестной проверкой используйте методы RegressionPartitionedModel класс. Для получения информации о методах этого класса см. RegressionPartitionedModel страница класса.

Примеры

свернуть все

В этом примере используются данные abalone [1], [2] из репозитория машинного обучения UCI [3]. Загрузите данные и сохраните их в текущей папке с именем abalone.data.

Сохраните данные в таблице. Просмотрите первые семь строк.

tbl = readtable('abalone.data','Filetype','text',...
     'ReadVariableNames',false);
tbl.Properties.VariableNames = {'Sex','Length','Diameter','Height',...
     'WWeight','SWeight','VWeight','ShWeight','NoShellRings'};
tbl(1:7,:)
ans = 

    Sex    Length    Diameter    Height    WWeight    SWeight    VWeight    ShWeight    NoShellRings
    ___    ______    ________    ______    _______    _______    _______    ________    ____________

    'M'    0.455     0.365       0.095      0.514     0.2245      0.101      0.15       15          
    'M'     0.35     0.265        0.09     0.2255     0.0995     0.0485      0.07        7          
    'F'     0.53      0.42       0.135      0.677     0.2565     0.1415      0.21        9          
    'M'     0.44     0.365       0.125      0.516     0.2155      0.114     0.155       10          
    'I'     0.33     0.255        0.08      0.205     0.0895     0.0395     0.055        7          
    'I'    0.425       0.3       0.095     0.3515      0.141     0.0775      0.12        8          
    'F'     0.53     0.415        0.15     0.7775      0.237     0.1415      0.33       20

В наборе данных 4177 наблюдений. Цель - предсказать возраст абалона из восьми физических измерений. Последняя переменная, число оболочечных колец показывает возраст абалона. Первый предиктор - категориальная переменная. Последней переменной в таблице является переменная ответа.

Подгонка модели GPR с использованием метода подмножества регрессоров для оценки параметров и полностью независимого условного метода для прогнозирования. Стандартизируйте предикторы.

gprMdl = fitrgp(tbl,'NoShellRings','KernelFunction','ardsquaredexponential',...
      'FitMethod','sr','PredictMethod','fic','Standardize',1)

grMdl = 

  RegressionGP
       PredictorNames: {1x8 cell}
         ResponseName: 'Var9'
    ResponseTransform: 'none'
      NumObservations: 4177
       KernelFunction: 'ARDSquaredExponential'
    KernelInformation: [1x1 struct]
        BasisFunction: 'Constant'
                 Beta: 10.9148
                Sigma: 2.0243
    PredictorLocation: [10x1 double]
       PredictorScale: [10x1 double]
                Alpha: [1000x1 double]
     ActiveSetVectors: [1000x10 double]
        PredictMethod: 'FIC'
        ActiveSetSize: 1000
            FitMethod: 'SR'
      ActiveSetMethod: 'Random'
    IsActiveSetVector: [4177x1 logical]
        LogLikelihood: -9.0013e+03
     ActiveSetHistory: [1x1 struct]
       BCDInformation: []

Спрогнозировать ответы с использованием обученной модели.

ypred = resubPredict(gprMdl);

Постройте график истинного ответа и прогнозируемых ответов.

figure();
plot(tbl.NoShellRings,'r.');
hold on
plot(ypred,'b');
xlabel('x');
ylabel('y');
legend({'data','predictions'},'Location','Best');
axis([0 4300 0 30]);
hold off;

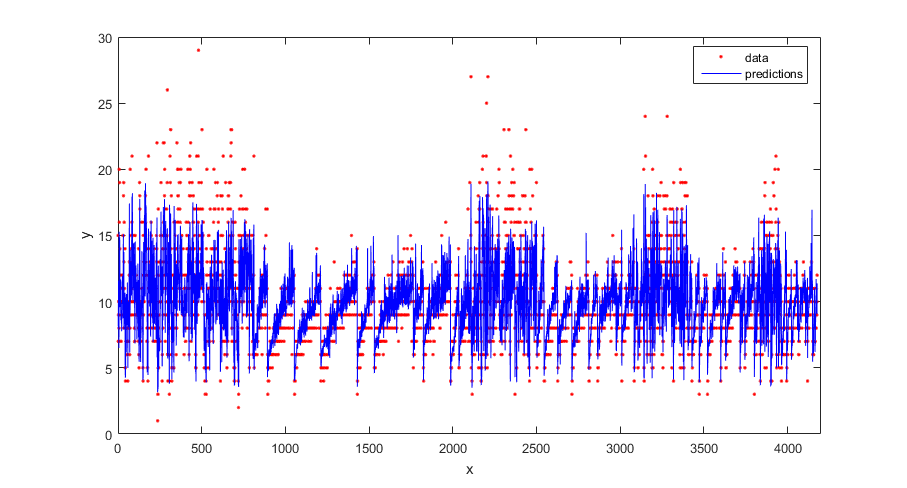
Вычислите регрессионную потерю на обучающих данных (потерю повторного замещения) для обученной модели.

L = resubLoss(gprMdl)
L =

    4.0064
Открыть сценарий в реальном времени

Создать образец данных. 

rng(0,'twister'); % For reproducibility
n = 1000;
x = linspace(-10,10,n)';
y = 1 + x*5e-2 + sin(x)./x + 0.2*randn(n,1);

Подгонка модели GPR с использованием линейной базисной функции и метода точного подбора для оценки параметров. Также используйте метод точного прогнозирования. 

gprMdl = fitrgp(x,y,'Basis','linear',...
      'FitMethod','exact','PredictMethod','exact');

Предсказать ответ, соответствующий строкам x (прогнозы повторного замещения) с использованием обученной модели. 

ypred = resubPredict(gprMdl);

Постройте график истинной реакции с предсказанными значениями. 

plot(x,y,'b.');
hold on;
plot(x,ypred,'r','LineWidth',1.5);
xlabel('x');
ylabel('y');
legend('Data','GPR predictions');
hold off

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Data, GPR predictions.

Открыть сценарий в реальном времени

Загрузите образцы данных. 

load('gprdata2.mat')

Данные имеют одну предикторную переменную и непрерывный ответ. Это смоделированные данные.

Поместите модель GPR, используя квадратную экспоненциальную функцию ядра с параметрами ядра по умолчанию. 

gprMdl1 = fitrgp(x,y,'KernelFunction','squaredexponential');

Теперь поместите вторую модель, где укажите начальные значения параметров ядра. 

sigma0 = 0.2;
kparams0 = [3.5, 6.2];
gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential',...
     'KernelParameters',kparams0,'Sigma',sigma0);

Вычислите прогнозы повторного замещения для обеих моделей. 

ypred1 = resubPredict(gprMdl1);
ypred2 = resubPredict(gprMdl2);

Постройте график прогнозов ответа от обеих моделей и ответов в данных обучения. 

figure();
plot(x,y,'r.');
hold on
plot(x,ypred1,'b');
plot(x,ypred2,'g');
xlabel('x');
ylabel('y');
legend({'data','default kernel parameters',...
'kparams0 = [3.5,6.2], sigma0 = 0.2'},...
'Location','Best');
title('Impact of initial kernel parameter values');
hold off

Figure contains an axes. The axes with title Impact of initial kernel parameter values contains 3 objects of type line. These objects represent data, default kernel parameters, kparams0 = [3.5,6.2], sigma0 = 0.2.

Предельная вероятность того, что fitrgp максимизирует для оценки параметров GPR имеет множество локальных решений; решение, к которому он сходится, зависит от начальной точки. Каждое локальное решение соответствует конкретной интерпретации данных. В этом примере решение с исходными параметрами ядра по умолчанию соответствует низкочастотному сигналу с высоким уровнем шума, тогда как второе решение с пользовательскими начальными параметрами ядра соответствует высокочастотному сигналу с низким уровнем шума.

Открыть сценарий в реальном времени

Загрузите образцы данных. 

load('gprdata.mat')

Существует шесть непрерывных переменных предиктора. В наборе учебных данных 500 наблюдений и 100 наблюдений в наборе тестовых данных. Это смоделированные данные.

Поместите модель GPR с использованием квадратной экспоненциальной функции ядра с отдельной шкалой длины для каждого предиктора. Эта ковариационная функция определяется как:

k (xi, xj 'start) = startf2exp [- 12∑m=1d (xim-xjm) 2startm2].

где startm представляет шкалу длины для предиктора m, m = 1, 2,..., d и startf - среднеквадратичное отклонение сигнала. Неограниченная параметризация

startm = logstartm, форма = 1,2,..., dstartd + 1 = logstartf.

Инициализировать шкалы длины функции ядра при 10 и среднеквадратических отклонениях сигнала и шума при среднеквадратическом отклонении отклика. 

sigma0 = std(ytrain);
sigmaF0 = sigma0;
d = size(Xtrain,2);
sigmaM0 = 10*ones(d,1);

Подгоните модель GPR, используя начальные значения параметров ядра. Стандартизируйте предикторы в данных обучения. Используйте методы точного подбора и прогнозирования. 

gprMdl = fitrgp(Xtrain,ytrain,'Basis','constant','FitMethod','exact',...
'PredictMethod','exact','KernelFunction','ardsquaredexponential',...
'KernelParameters',[sigmaM0;sigmaF0],'Sigma',sigma0,'Standardize',1);

Вычислите потери регрессии на тестовых данных. 

L = loss(gprMdl,Xtest,ytest)
L = 0.6919

Доступ к информации о ядре. 

gprMdl.KernelInformation
ans = struct with fields:
                    Name: 'ARDSquaredExponential'
        KernelParameters: [7x1 double]
    KernelParameterNames: {7x1 cell}

Отображение имен параметров ядра. 

gprMdl.KernelInformation.KernelParameterNames
ans = 7x1 cell
    {'LengthScale1'}
    {'LengthScale2'}
    {'LengthScale3'}
    {'LengthScale4'}
    {'LengthScale5'}
    {'LengthScale6'}
    {'SigmaF'      }

Отображение параметров ядра. 

sigmaM = gprMdl.KernelInformation.KernelParameters(1:end-1,1)
sigmaM = 6×1
104 ×

    0.0004
    0.0007
    0.0004
    5.2709
    0.1018
    0.0056


sigmaF = gprMdl.KernelInformation.KernelParameters(end)
sigmaF = 28.1721

sigma  = gprMdl.Sigma
sigma = 0.8162

Постройте журнал усвоенных шкал длины. 

figure()
plot((1:d)',log(sigmaM),'ro-');
xlabel('Length scale number');
ylabel('Log of length scale');

Figure contains an axes. The axes contains an object of type line.

Логарифмическая шкала длины для 4-й и 5-й прогнозирующих переменных высока по сравнению с остальными. Эти переменные предиктора, по-видимому, не так влиятельны на ответ, как другие переменные предиктора.

Подгоните модель GPR без использования 4-й и 5-й переменных в качестве переменных предиктора. 

X = [Xtrain(:,1:3) Xtrain(:,6)];
sigma0 = std(ytrain);
sigmaF0 = sigma0;
d = size(X,2);
sigmaM0 = 10*ones(d,1);

gprMdl = fitrgp(X,ytrain,'Basis','constant','FitMethod','exact',...
'PredictMethod','exact','KernelFunction','ardsquaredexponential',...
'KernelParameters',[sigmaM0;sigmaF0],'Sigma',sigma0,'Standardize',1);

Вычислите ошибку регрессии для данных теста. 

xtest = [Xtest(:,1:3) Xtest(:,6)];
L = loss(gprMdl,xtest,ytest)
L = 0.6928

Потеря аналогична той, когда все переменные используются в качестве предикторных переменных.

Вычислите прогнозируемый отклик для тестовых данных. 

 ypred = predict(gprMdl,xtest);

Постройте график исходного ответа вместе с подходящими значениями. 

figure;
plot(ytest,'r');
hold on;
plot(ypred,'b');
legend('True response','GPR predicted values','Location','Best');
hold off

Figure contains an axes. The axes contains 2 objects of type line. These objects represent True response, GPR predicted values.

Открыть сценарий в реальном времени

В этом примере показано, как оптимизировать гиперпараметры автоматически с помощью fitrgp. В примере используется gprdata2 данные, поставляемые с программным обеспечением.

Загрузите данные.

load('gprdata2.mat')

Данные имеют одну предикторную переменную и непрерывный ответ. Это смоделированные данные.

Поместите модель GPR, используя квадратную экспоненциальную функцию ядра с параметрами ядра по умолчанию.

gprMdl1 = fitrgp(x,y,'KernelFunction','squaredexponential');

Найдите гиперпараметры, которые минимизируют пятикратные потери при перекрестной проверке, используя автоматическую оптимизацию гиперпараметров.

Для воспроизводимости задайте случайное начальное число и используйте 'expected-improvement-plus' функция приобретения.

rng default
gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential',...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',...
    struct('AcquisitionFunctionName','expected-improvement-plus'));
|======================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |        Sigma |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |
|======================================================================================|
|    1 | Best   |     0.29417 |      4.8721 |     0.29417 |     0.29417 |    0.0015045 |
|    2 | Best   |    0.037898 |      2.9698 |    0.037898 |    0.060792 |      0.14147 |
|    3 | Accept |      1.5693 |      2.2862 |    0.037898 |    0.040633 |       25.279 |
|    4 | Accept |     0.29417 |      3.9255 |    0.037898 |    0.037984 |    0.0001091 |
|    5 | Accept |     0.29393 |       3.575 |    0.037898 |    0.038029 |     0.029932 |
|    6 | Accept |     0.13152 |      3.2312 |    0.037898 |    0.038127 |      0.37127 |
|    7 | Best   |    0.037785 |       5.189 |    0.037785 |    0.037728 |      0.18116 |
|    8 | Accept |     0.03783 |      4.3223 |    0.037785 |    0.036524 |      0.16251 |
|    9 | Accept |    0.037833 |      4.9764 |    0.037785 |    0.036854 |      0.16159 |
|   10 | Accept |    0.037835 |      5.3911 |    0.037785 |    0.037052 |      0.16072 |
|   11 | Accept |     0.29417 |       5.427 |    0.037785 |     0.03705 |   0.00038214 |
|   12 | Accept |     0.42256 |      3.4003 |    0.037785 |     0.03696 |       3.2067 |
|   13 | Accept |     0.03786 |      3.6868 |    0.037785 |    0.037087 |      0.15245 |
|   14 | Accept |     0.29417 |      4.3881 |    0.037785 |    0.037043 |    0.0063584 |
|   15 | Accept |     0.42302 |      3.1663 |    0.037785 |     0.03725 |       1.2221 |
|   16 | Accept |    0.039486 |      2.6376 |    0.037785 |    0.037672 |      0.10069 |
|   17 | Accept |    0.038591 |       3.091 |    0.037785 |    0.037687 |      0.12077 |
|   18 | Accept |    0.038513 |      2.4893 |    0.037785 |    0.037696 |       0.1227 |
|   19 | Best   |    0.037757 |      2.0492 |    0.037757 |    0.037572 |      0.19621 |
|   20 | Accept |    0.037787 |       3.169 |    0.037757 |    0.037601 |      0.18068 |
|======================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |        Sigma |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |
|======================================================================================|
|   21 | Accept |     0.44917 |      2.4079 |    0.037757 |     0.03766 |       8.7818 |
|   22 | Accept |    0.040201 |      3.4579 |    0.037757 |    0.037601 |     0.075414 |
|   23 | Accept |    0.040142 |      3.7027 |    0.037757 |    0.037607 |     0.087198 |
|   24 | Accept |     0.29417 |      5.0095 |    0.037757 |     0.03758 |    0.0031018 |
|   25 | Accept |     0.29417 |      5.1286 |    0.037757 |    0.037555 |   0.00019545 |
|   26 | Accept |     0.29417 |      4.7136 |    0.037757 |    0.037582 |     0.013608 |
|   27 | Accept |     0.29417 |      3.9032 |    0.037757 |    0.037556 |   0.00076147 |
|   28 | Accept |     0.42162 |      1.9316 |    0.037757 |    0.037854 |       0.6791 |
|   29 | Best   |    0.037704 |      2.7232 |    0.037704 |    0.037908 |       0.2367 |
|   30 | Accept |    0.037725 |      3.5853 |    0.037704 |    0.037881 |      0.21743 |

Figure contains an axes. The axes with title Min objective vs. Number of function evaluations contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

Figure contains an axes. The axes with title Objective function model contains 8 objects of type line. These objects represent Observed points, Model mean, Model error bars, Noise error bars, Next point, Model minimum feasible.

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 140.3815 seconds
Total objective function evaluation time: 110.8067

Best observed feasible point:
    Sigma 
    ______

    0.2367

Observed objective function value = 0.037704
Estimated objective function value = 0.038223
Function evaluation time = 2.7232

Best estimated feasible point (according to models):
     Sigma 
    _______

    0.16159

Estimated objective function value = 0.037881
Estimated function evaluation time = 3.3839

Сравните соответствия перед и после оптимизации.

ypred1 = resubPredict(gprMdl1);
ypred2 = resubPredict(gprMdl2);

figure();
plot(x,y,'r.');
hold on
plot(x,ypred1,'b');
plot(x,ypred2,'k','LineWidth',2);
xlabel('x');
ylabel('y');
legend({'data','Initial Fit','Optimized Fit'},'Location','Best');
title('Impact of Optimization');
hold off

Figure contains an axes. The axes with title Impact of Optimization contains 3 objects of type line. These objects represent data, Initial Fit, Optimized Fit.

В этом примере используются данные abalone [1], [2] из репозитория машинного обучения UCI [3]. Загрузите данные и сохраните их в текущей папке с именем abalone.data.

Сохранение данных в table. Просмотрите первые семь строк.

tbl = readtable('abalone.data','Filetype','text','ReadVariableNames',false);
tbl.Properties.VariableNames = {'Sex','Length','Diameter','Height','WWeight','SWeight','VWeight','ShWeight','NoShellRings'};
tbl(1:7,:)
ans = 

    Sex    Length    Diameter    Height    WWeight    SWeight    VWeight    ShWeight    NoShellRings
    ___    ______    ________    ______    _______    _______    _______    ________    ____________

    'M'    0.455     0.365       0.095      0.514     0.2245      0.101      0.15       15          
    'M'     0.35     0.265        0.09     0.2255     0.0995     0.0485      0.07        7          
    'F'     0.53      0.42       0.135      0.677     0.2565     0.1415      0.21        9          
    'M'     0.44     0.365       0.125      0.516     0.2155      0.114     0.155       10          
    'I'     0.33     0.255        0.08      0.205     0.0895     0.0395     0.055        7          
    'I'    0.425       0.3       0.095     0.3515      0.141     0.0775      0.12        8          
    'F'     0.53     0.415        0.15     0.7775      0.237     0.1415      0.33       20

В наборе данных 4177 наблюдений. Цель - предсказать возраст абалона из восьми физических измерений. Последняя переменная, число оболочечных колец показывает возраст абалона. Первый предиктор - категориальная переменная. Последней переменной в таблице является переменная ответа.

Обучение перекрестно проверенной модели GPR с использованием 25% данных для проверки.

rng('default') % For reproducibility
cvgprMdl = fitrgp(tbl,'NoShellRings','Standardize',1,'Holdout',0.25);

Вычислите средние потери на складках, используя модели, обученные на нестандартных наблюдениях.

kfoldLoss(cvgprMdl)

ans =
   4.6409

Спрогнозировать ответы для устаревших данных.

ypred = kfoldPredict(cvgprMdl);

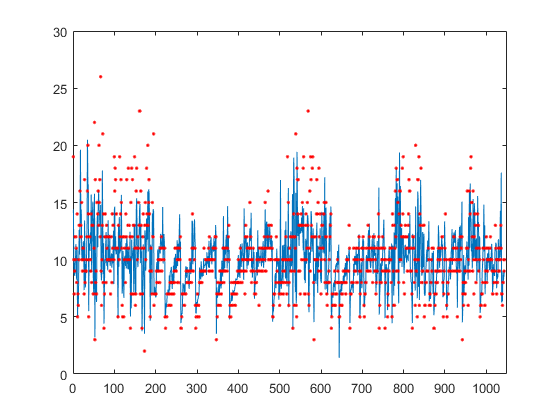
Постройте график истинных ответов, используемых для тестирования, и прогнозов.

figure();
plot(ypred(cvgprMdl.Partition.test));
hold on;
y = table2array(tbl(:,end));
plot(y(cvgprMdl.Partition.test),'r.');
axis([0 1050 0 30]);
xlabel('x')
ylabel('y')
hold off;

Открыть сценарий в реальном времени

Создайте образец данных.

rng(0,'twister'); % For reproducibility
n = 1000;
x = linspace(-10,10,n)';
y = 1 + x*5e-2 + sin(x)./x + 0.2*randn(n,1);

Определите квадратную экспоненциальную функцию ядра как пользовательскую функцию ядра.

Можно вычислить квадратную экспоненциальную функцию ядра как

k (xi, xj 'start) = startf2exp (-12 (xi-xj) T (xi-xj) startl2),

где startf - среднеквадратичное отклонение сигнала, startl - шкала длины. И startf, и startl должны быть больше нуля. Это условие может быть проведено в жизнь добровольной параметризацией, σl=exp (θ (1)) и σf=exp (θ (2)), для некоторого добровольного вектора параметризации θ.

Следовательно, можно определить квадратную экспоненциальную функцию ядра как пользовательскую функцию ядра следующим образом:

kfcn = @(XN,XM,theta) (exp(theta(2))^2)*exp(-(pdist2(XN,XM).^2)/(2*exp(theta(1))^2));

Здесь pdist2(XN,XM).^2 вычисляет матрицу расстояний.

Поместите модель GPR с помощью пользовательской функции ядра, kfcn. Укажите начальные значения параметров ядра (Поскольку используется пользовательская функция ядра, необходимо указать начальные значения для неограниченного вектора параметризации, theta).

theta0 = [1.5,0.2];
gprMdl = fitrgp(x,y,'KernelFunction',kfcn,'KernelParameters',theta0);

fitrgp использует аналитические производные для оценки параметров при использовании встроенной функции ядра, тогда как при использовании пользовательской функции ядра использует числовые производные.

Вычислите потерю повторного замещения для этой модели. 

L = resubLoss(gprMdl)
L = 0.0391

Подгоните модель GPR с помощью опции встроенной возведенной в квадрат экспоненциальной функции ядра. Укажите начальные значения параметров ядра (поскольку вы используете встроенную пользовательскую функцию ядра и указываете начальные значения параметров, вы должны предоставить начальные значения для стандартного отклонения сигнала и шкалы (шкал) длины ).

sigmaL0 = exp(1.5);
sigmaF0 = exp(0.2);
gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential','KernelParameters',[sigmaL0,sigmaF0]);

Вычислите потерю повторного замещения для этой модели. 

L2 = resubLoss(gprMdl2)
L2 = 0.0391

Значения двух потерь совпадают с ожидаемыми.

Открыть сценарий в реальном времени

Обучить модель GPR сгенерированным данным со многими предикторами. Укажите начальный размер шага для оптимизатора LBFGS.

Задайте начальное число и тип генератора случайных чисел для воспроизводимости результатов.

rng(0,'twister'); % For reproducibility

Создайте данные выборки с 300 наблюдениями и 3000 предикторами, где переменная ответа зависит от 4, 7 и 13 предикторов.

N = 300;
P = 3000;
X = rand(N,P);
y = cos(X(:,7)) + sin(X(:,4).*X(:,13)) + 0.1*randn(N,1);

Установите начальные значения для параметров ядра.

sigmaL0 = sqrt(P)*ones(P,1); % Length scale for predictors
sigmaF0 = 1; % Signal standard deviation

Установить начальное среднеквадратичное отклонение шума в 1.

sigmaN0 = 1;

Определить 1e-2 в качестве допуска окончания для нормы относительного градиента.

opts = statset('fitrgp');
opts.TolFun = 1e-2;

Подгонка модели GPR с использованием начальных значений параметров ядра, начального среднеквадратического отклонения шума и функции автоматического определения релевантности (ARD) в квадрате экспоненциального ядра.

Укажите начальный размер шага как 1 для определения начального гессенского приближения для оптимизатора LBFGS.

gpr = fitrgp(X,y,'KernelFunction','ardsquaredexponential','Verbose',1, ...
    'Optimizer','lbfgs','OptimizerOptions',opts, ...
    'KernelParameters',[sigmaL0;sigmaF0],'Sigma',sigmaN0,'InitialStepSize',1);
o Parameter estimation: FitMethod = Exact, Optimizer = lbfgs

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 |  3.004966e+02 |   2.569e+02 |   0.000e+00 |        |   3.893e-03 |   0.000e+00 |   YES  |
|        1 |  9.525779e+01 |   1.281e+02 |   1.003e+00 |    OK  |   6.913e-03 |   1.000e+00 |   YES  |
|        2 |  3.972026e+01 |   1.647e+01 |   7.639e-01 |    OK  |   4.718e-03 |   5.000e-01 |   YES  |
|        3 |  3.893873e+01 |   1.073e+01 |   1.057e-01 |    OK  |   3.243e-03 |   1.000e+00 |   YES  |
|        4 |  3.859904e+01 |   5.659e+00 |   3.282e-02 |    OK  |   3.346e-03 |   1.000e+00 |   YES  |
|        5 |  3.748912e+01 |   1.030e+01 |   1.395e-01 |    OK  |   1.460e-03 |   1.000e+00 |   YES  |
|        6 |  2.028104e+01 |   1.380e+02 |   2.010e+00 |    OK  |   2.326e-03 |   1.000e+00 |   YES  |
|        7 |  2.001849e+01 |   1.510e+01 |   9.685e-01 |    OK  |   2.344e-03 |   1.000e+00 |   YES  |
|        8 | -7.706109e+00 |   8.340e+01 |   1.125e+00 |    OK  |   5.771e-04 |   1.000e+00 |   YES  |
|        9 | -1.786074e+01 |   2.323e+02 |   2.647e+00 |    OK  |   4.217e-03 |   1.250e-01 |   YES  |
|       10 | -4.058422e+01 |   1.972e+02 |   6.796e-01 |    OK  |   7.035e-03 |   1.000e+00 |   YES  |
|       11 | -7.850209e+01 |   4.432e+01 |   8.335e-01 |    OK  |   3.099e-03 |   1.000e+00 |   YES  |
|       12 | -1.312162e+02 |   3.334e+01 |   1.277e+00 |    OK  |   5.432e-02 |   1.000e+00 |   YES  |
|       13 | -2.005064e+02 |   9.519e+01 |   2.828e+00 |    OK  |   5.292e-03 |   1.000e+00 |   YES  |
|       14 | -2.070150e+02 |   1.898e+01 |   1.641e+00 |    OK  |   6.817e-03 |   1.000e+00 |   YES  |
|       15 | -2.108086e+02 |   3.793e+01 |   7.685e-01 |    OK  |   3.479e-03 |   1.000e+00 |   YES  |
|       16 | -2.122920e+02 |   7.057e+00 |   1.591e-01 |    OK  |   2.055e-03 |   1.000e+00 |   YES  |
|       17 | -2.125610e+02 |   4.337e+00 |   4.818e-02 |    OK  |   1.974e-03 |   1.000e+00 |   YES  |
|       18 | -2.130162e+02 |   1.178e+01 |   8.891e-02 |    OK  |   2.856e-03 |   1.000e+00 |   YES  |
|       19 | -2.139378e+02 |   1.933e+01 |   2.371e-01 |    OK  |   1.029e-02 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       20 | -2.151111e+02 |   1.550e+01 |   3.015e-01 |    OK  |   2.765e-02 |   1.000e+00 |   YES  |
|       21 | -2.173046e+02 |   5.856e+00 |   6.537e-01 |    OK  |   1.414e-02 |   1.000e+00 |   YES  |
|       22 | -2.201781e+02 |   8.918e+00 |   8.484e-01 |    OK  |   6.381e-03 |   1.000e+00 |   YES  |
|       23 | -2.288858e+02 |   4.846e+01 |   2.311e+00 |    OK  |   2.661e-03 |   1.000e+00 |   YES  |
|       24 | -2.392171e+02 |   1.190e+02 |   6.283e+00 |    OK  |   8.113e-03 |   1.000e+00 |   YES  |
|       25 | -2.511145e+02 |   1.008e+02 |   1.198e+00 |    OK  |   1.605e-02 |   1.000e+00 |   YES  |
|       26 | -2.742547e+02 |   2.207e+01 |   1.231e+00 |    OK  |   3.191e-03 |   1.000e+00 |   YES  |
|       27 | -2.849931e+02 |   5.067e+01 |   3.660e+00 |    OK  |   5.184e-03 |   1.000e+00 |   YES  |
|       28 | -2.899797e+02 |   2.068e+01 |   1.162e+00 |    OK  |   6.270e-03 |   1.000e+00 |   YES  |
|       29 | -2.916723e+02 |   1.816e+01 |   3.213e-01 |    OK  |   1.415e-02 |   1.000e+00 |   YES  |
|       30 | -2.947674e+02 |   6.965e+00 |   1.126e+00 |    OK  |   6.339e-03 |   1.000e+00 |   YES  |
|       31 | -2.962491e+02 |   1.349e+01 |   2.352e-01 |    OK  |   8.999e-03 |   1.000e+00 |   YES  |
|       32 | -3.004921e+02 |   1.586e+01 |   9.880e-01 |    OK  |   3.940e-02 |   1.000e+00 |   YES  |
|       33 | -3.118906e+02 |   1.889e+01 |   3.318e+00 |    OK  |   1.213e-01 |   1.000e+00 |   YES  |
|       34 | -3.189215e+02 |   7.086e+01 |   3.070e+00 |    OK  |   8.095e-03 |   1.000e+00 |   YES  |
|       35 | -3.245557e+02 |   4.366e+00 |   1.397e+00 |    OK  |   2.718e-03 |   1.000e+00 |   YES  |
|       36 | -3.254613e+02 |   3.751e+00 |   6.546e-01 |    OK  |   1.004e-02 |   1.000e+00 |   YES  |
|       37 | -3.262823e+02 |   4.011e+00 |   2.026e-01 |    OK  |   2.441e-02 |   1.000e+00 |   YES  |
|       38 | -3.325606e+02 |   1.773e+01 |   2.427e+00 |    OK  |   5.234e-02 |   1.000e+00 |   YES  |
|       39 | -3.350374e+02 |   1.201e+01 |   1.603e+00 |    OK  |   2.674e-02 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       40 | -3.379112e+02 |   5.280e+00 |   1.393e+00 |    OK  |   1.177e-02 |   1.000e+00 |   YES  |
|       41 | -3.389136e+02 |   3.061e+00 |   7.121e-01 |    OK  |   2.935e-02 |   1.000e+00 |   YES  |
|       42 | -3.401070e+02 |   4.094e+00 |   6.224e-01 |    OK  |   3.399e-02 |   1.000e+00 |   YES  |
|       43 | -3.436291e+02 |   8.833e+00 |   1.707e+00 |    OK  |   5.231e-02 |   1.000e+00 |   YES  |
|       44 | -3.456295e+02 |   5.891e+00 |   1.424e+00 |    OK  |   3.772e-02 |   1.000e+00 |   YES  |
|       45 | -3.460069e+02 |   1.126e+01 |   2.580e+00 |    OK  |   3.907e-02 |   1.000e+00 |   YES  |
|       46 | -3.481756e+02 |   1.546e+00 |   8.142e-01 |    OK  |   1.565e-02 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 1.546e+00
              Two norm of the final step     = 8.142e-01, TolX   = 1.000e-12
Relative infinity norm of the final gradient = 6.016e-03, TolFun = 1.000e-02
EXIT: Local minimum found.

o Alpha estimation: PredictMethod = Exact

Поскольку модель GPR использует ядро ARD со многими предикторами, использование приближения LBFGS к гессенскому является более эффективной памятью, чем хранение полной матрицы Гессена. Кроме того, использование начального размера шага для определения начального гессенского приближения может помочь ускорить оптимизацию.

Найдите веса предиктора, взяв экспоненту отрицательных усвоенных шкал длины. Нормализуйте веса.

sigmaL = gpr.KernelInformation.KernelParameters(1:end-1); % Learned length scales
weights = exp(-sigmaL); % Predictor weights
weights = weights/sum(weights); % Normalized predictor weights

Постройте график нормированных предикторных весов. 

figure;
semilogx(weights,'ro');
xlabel('Predictor index');
ylabel('Predictor weight');

Обученная модель GPR присваивает наибольшие веса 4-му, 7-му и 13-му предикторам. Неактуальные предикторы имеют веса, близкие к нулю.

Входные аргументы

свернуть все

Образец данных, используемых для обучения модели, указанный как table. Каждая строка Tbl соответствует одному наблюдению, и каждый столбец соответствует одной переменной. Tbl содержит переменные предиктора, и, возможно, он также может содержать один столбец для переменной ответа. Многозначные переменные и массивы ячеек, отличные от массивов ячеек символьных векторов, не допускаются.

  • Если Tbl содержит переменную ответа, и вы хотите использовать все оставшиеся переменные в качестве предикторов, а затем указать переменную ответа с помощью ResponseVarName.

  • Если Tbl содержит переменную ответа, и при обучении модели необходимо использовать только подмножество предикторов, затем указать переменную ответа и переменные предиктора, используя formula.

  • Если Tbl не содержит переменную ответа, затем укажите переменную ответа, используя y. Длина переменной ответа и количество строк в Tbl должно быть равным.

Для получения дополнительной информации о table тип данных, см. table.

Если данные предиктора содержат категориальные переменные, то fitrgp создает фиктивные переменные. Для получения более подробной информации см. CategoricalPredictors.

Типы данных: table

Имя переменной ответа, указанное как имя переменной в Tbl. Необходимо указать ResponseVarName в виде вектора символов или строкового скаляра. Например, если переменная ответа y хранится в Tbl (как Tbl.y), затем укажите его как 'y'. В противном случае программа обрабатывает все столбцы Tbl, в том числе y, в качестве предикторов при обучении модели.

Типы данных: char | string

Переменные ответа и предиктора для использования в обучении модели, определенные как вектор символов или строковый скаляр в виде 'y~x1+x2+x3'. В этой форме y представляет переменную ответа; x1, x2, x3 представляют переменные предиктора для использования при обучении модели.

Используйте формулу, если необходимо указать подмножество переменных в Tbl в качестве предикторов для использования при обучении модели. Если задать формулу, то все переменные, которые не появляются в formula не используются для обучения модели.

Имена переменных в формуле должны быть обоими именами переменных в Tbl (Tbl.Properties.VariableNames) и допустимые идентификаторы MATLAB ®. Имена переменных можно проверить вTbl с помощью isvarname функция. Если имена переменных недопустимы, их можно преобразовать с помощью matlab.lang.makeValidName функция.

Формула не указывает форму BasisFunction.

Пример: 'PetalLength~PetalWidth+Species' определяет переменную PetalLength в качестве переменной ответа, и PetalWidth и Species в качестве переменных предиктора.

Типы данных: char | string

Данные предиктора для модели GPR, определенные как матрица n-за-d. n - количество наблюдений (строк), а d - число предикторов (столбцов).

Длина y и количество строк X должно быть равным.

Чтобы указать имена предикторов в порядке их появления в X, используйте PredictorNames аргумент пары имя-значение.

Типы данных: double

Данные ответа для модели GPR, указанные как вектор n-by-1. Вы можете опустить y если вы предоставляете Tbl данные обучения, которые также включают y. В этом случае используйте ResponseVarName для идентификации переменной ответа или использования formula для идентификации переменных ответа и предиктора.

Типы данных: double

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Пример: 'FitMethod','sr','BasisFunction','linear','ActiveSetMethod','sgma','PredictMethod','fic' обучает модель GPR с использованием метода аппроксимации подмножества регрессоров для оценки параметров, использует линейную базисную функцию, использует для активного выбора разреженную жадную матричную аппроксимацию и полностью независимый метод условной аппроксимации для прогнозирования.

Примечание

Нельзя использовать любой аргумент пары имя-значение перекрестной проверки вместе с 'OptimizeHyperparameters' аргумент пары имя-значение. Можно изменить перекрестную проверку для 'OptimizeHyperparameters' только с помощью 'HyperparameterOptimizationOptions' аргумент пары имя-значение.

Установка

свернуть все

Метод оценки параметров модели GPR, определяемый как разделенная запятыми пара, состоящая из 'FitMethod' и одно из следующих.

Метод подгонкиОписание
'none'Нет оценки, используйте начальные значения параметров в качестве известных значений параметров.
'exact'Точная гауссова регрессия процесса. По умолчанию n ≤ 2000, где n - количество наблюдений.
'sd'Подмножество аппроксимации точек данных. По умолчанию n > 2000, где n - количество наблюдений.
'sr'Подмножество аппроксимации регрессоров.
'fic'Полностью независимое условное приближение.

Пример: 'FitMethod','fic'

Явная основа в модели GPR, указанная как пара, разделенная запятыми, состоящая из 'BasisFunction' и одно из следующих. Если n - число наблюдений, базисная функция добавляет в модель член H * β, где H - базисная матрица, а β - вектор p-by-1 базисных коэффициентов.

Явная основаБазисная матрица
'none'Пустая матрица.
'constant'

H = 1

(вектор n-by-1 из 1s, где n - число наблюдений)

'linear'

H = [1, X]

'pureQuadratic'

H = [1, X, X2],

где

X2 = [x112x122x1d2x212x222x2d2  xn12xn22xnd2].

Дескриптор функции

Дескриптор функции, hfcn, что fitrgp вызовы в виде:

H = hfcn (X),

где X - матрица n-за-d предикторов, а H - матрица n-за-p базисных функций.

Пример: 'BasisFunction','pureQuadratic'

Типы данных: char | string | function_handle

Начальное значение коэффициентов для явного базиса, определяемого как разделенная запятыми пара, состоящая из 'Beta' и вектор p-by-1, где p - количество столбцов в базовой матрице H.

Базисная матрица зависит от выбора явной базисной функции следующим образом (также см. BasisFunction).

fitrgp использует начальные значения коэффициентов в качестве известных значений коэффициентов, только когда FitMethod является 'none'.

Типы данных: double

Начальное значение среднеквадратического отклонения шума модели гауссова процесса, указанное как пара, разделенная запятыми, состоящая из 'Sigma' и положительное скалярное значение.

Пример: 'Sigma',2

Типы данных: double

Постоянное значение Sigma для шумового стандартного отклонения модели гауссова процесса, заданного как логический скаляр. Когда ConstantSigma является true, fitrgp не оптимизирует значение Sigma, но вместо этого принимает начальное значение в качестве значения во всех своих вычислениях.

Пример: 'ConstantSigma',true

Типы данных: logical

Нижняя граница среднеквадратического отклонения шума, указанная как разделенная запятыми пара, состоящая из 'SigmaLowerBound' и положительное скалярное значение.

Пример: 'SigmaLowerBound',0.02

Типы данных: double

Список категориальных предикторов, указанный как одно из значений в этой таблице.

СтоимостьОписание
Вектор положительных целых чисел

Каждая запись в векторе представляет собой значение индекса, соответствующее столбцу данных предиктора, который содержит категориальную переменную. Значения индекса находятся в диапазоне от 1 до p, где p - количество предикторов, используемых для обучения модели.

Если fitrgp использует подмножество входных переменных в качестве предикторов, затем функция индексирует предикторы, используя только подмножество. 'CategoricalPredictors' значения не подсчитывают переменную отклика, переменную веса наблюдения и любые другие переменные, которые функция не использует.

Логический вектор

A true ввод означает, что соответствующий столбец данных предиктора является категориальной переменной. Длина вектора равна p.

Символьная матрицаКаждая строка матрицы является именем предикторной переменной. Имена должны соответствовать записям в PredictorNames. Поместите имена с дополнительными пробелами, чтобы каждая строка символьной матрицы имела одинаковую длину.
Строковый массив или массив ячеек символьных векторовКаждый элемент массива является именем переменной предиктора. Имена должны соответствовать записям в PredictorNames.
'all'Все предикторы категоричны.

По умолчанию, если данные предиктора находятся в таблице (Tbl), fitrgp предполагает, что переменная категорична, если она является логическим вектором, категориальным вектором, символьным массивом, строковым массивом или массивом ячеек символьных векторов. Если данные предиктора являются матрицей (X), fitrgp предполагает, что все предикторы непрерывны. Чтобы определить любые другие предикторы как категориальные предикторы, укажите их с помощью 'CategoricalPredictors' аргумент «имя-значение».

Для выявленных категориальных предикторов fitrgp создает фиктивные переменные, используя две различные схемы, в зависимости от того, неупорядочена или упорядочена категориальная переменная. Для неупорядоченной категориальной переменной fitrgp создает одну фиктивную переменную для каждого уровня категориальной переменной. Для упорядоченной категориальной переменной fitrgp создает на одну фиктивную переменную меньше числа категорий. Дополнительные сведения см. в разделе Автоматическое создание фиктивных переменных.

Пример: 'CategoricalPredictors','all'

Типы данных: single | double | logical | char | string | cell

Индикатор для стандартизации данных, указанный как разделенная запятыми пара, состоящая из 'Standardize' и логическое значение.

Если установить 'Standardize',1затем программное обеспечение центрирует и масштабирует каждый столбец данных предиктора на среднее значение столбца и стандартное отклонение соответственно. Программное обеспечение не стандартизирует данные, содержащиеся в фиктивных столбцах переменных, которые оно генерирует для категориальных предикторов.

Пример: 'Standardize',1

Пример: 'Standardize',true

Типы данных: logical

Стандартное отклонение регуляризации для подмножества регрессоров разреженных методов ('sr') и полностью независимым условным ('fic'), указанная как пара, разделенная запятыми, состоящая из 'Regularization' и положительное скалярное значение.

Пример: 'Regularization',0.2

Типы данных: double

Способ вычисления логарифмического правдоподобия и градиента для оценки параметров с использованием подмножества регрессоров ('sr') и полностью независимым условным ('fic') методы аппроксимации, указанные как пара, разделенная запятыми, состоящая из 'ComputationMethod' и одно из следующих.

  • 'qr' - Используйте подход, основанный на факторизации QR, этот параметр обеспечивает лучшую точность.

  • 'v' - Использовать подход, основанный на V-методе. Этот параметр обеспечивает более быстрое вычисление логарифмических градиентов правдоподобия.

Пример: 'ComputationMethod','v'

Функция ядра (ковариация)

свернуть все

Форма ковариационной функции, определяемая как разделенная запятыми пара, состоящая из 'KernelFunction' и одно из следующих.

ФункцияОписание
'exponential'Экспоненциальное ядро.
'squaredexponential'Квадратное экспоненциальное ядро.
'matern32'Ядро матрицы с параметром 3/2.
'matern52'Ядро матрицы с параметром 5/2.
'rationalquadratic'Рациональное квадратичное ядро.
'ardexponential'Экспоненциальное ядро с отдельной шкалой длины на предиктор.
'ardsquaredexponential'Квадратное экспоненциальное ядро с отдельной шкалой длины на предсказатель.
'ardmatern32'Материновое ядро с параметром 3/2 и отдельной шкалой длины на предиктор.
'ardmatern52'Материновое ядро с параметром 5/2 и отдельной шкалой длины на предиктор.
'ardrationalquadratic'Рациональное квадратичное ядро с отдельной шкалой длины на предсказатель.
Дескриптор функцииДескриптор функции, который можно вызвать следующим образом:
Kmn = kfcn(Xm,Xn,theta)
где Xm - матрица m-на-d, Xn является матрицей n-за-d и Kmn - матрица m-на-n продуктов ядра, такая, что Kmn(i, j) является продуктом ядра междуXm(i,:) и Xn(j,:).
theta является вектором неограниченного параметра r-by-1 для kfcn.

Дополнительные сведения о функциях ядра см. в разделе Параметры функции Kernel (Covariance).

Пример: 'KernelFunction','matern32'

Типы данных: char | string | function_handle

Начальные значения параметров ядра, указанные как разделенная запятыми пара, состоящая из 'KernelParameters' и вектор. Размер вектора и значения зависят от формы ковариационной функции, определяемой KernelFunction аргумент пары имя-значение.

'KernelFunction''KernelParameters'
'exponential', 'squaredexponential', 'matern32', или 'matern52'Вектор 2 на 1 phi, где phi(1) содержит масштаб длины и phi(2) содержит стандартное отклонение сигнала.
По умолчанию начальное значение параметра шкалы длины представляет собой среднее значение стандартных отклонений предикторов, а стандартное отклонение сигнала представляет собой стандартное отклонение откликов, деленное на квадратный корень из 2. То есть
phi = [mean(std(X));std(y)/sqrt(2)]
'rationalquadratic'Вектор 3 на 1 phi, где phi(1) содержит масштаб длины, phi(2) содержит параметр scale-mission, и phi(3) содержит стандартное отклонение сигнала.
По умолчанию начальное значение параметра шкалы длины представляет собой среднее значение стандартных отклонений предикторов, а стандартное отклонение сигнала представляет собой стандартное отклонение откликов, деленное на квадратный корень из 2. Начальное значение по умолчанию для параметра scale-mission равно 1. То есть
phi = [mean(std(X));1;std(y)/sqrt(2)]
'ardexponential', 'ardsquaredexponential', 'ardmatern32', или 'ardmatern52'(d + 1) -by-1 векторphi, где phi(i) содержит шкалу длины для предиктора i, и phi(d+1) содержит стандартное отклонение сигнала. d - количество предикторных переменных после создания фиктивных переменных для категориальных переменных. Дополнительные сведения о создании фиктивных переменных см. в разделе CategoricalPredictors.
По умолчанию начальным значением параметров шкалы длины являются стандартные отклонения предикторов, а стандартным отклонением сигнала является стандартное отклонение откликов, деленное на квадратный корень из 2. То есть
phi = [std(X)';std(y)/sqrt(2)]
'ardrationalquadratic'(d + 2) -by-1 векторphi, где phi(i) содержит шкалу длины для предсказателя i, phi(d+1) содержит параметр scale-mission, и phi(d+2) содержит стандартное отклонение сигнала.
По умолчанию начальным значением параметров шкалы длины являются стандартные отклонения предикторов, а стандартным отклонением сигнала является стандартное отклонение откликов, деленное на квадратный корень из 2. Начальное значение по умолчанию для параметра scale-mission равно 1. То есть
phi = [std(X)';1;std(y)/sqrt(2)]
Дескриптор функциивектор r-by-1 как начальное значение вектора неограниченного параметра phi для пользовательской функции ядра kfcn.
Когда KernelFunction является дескриптором функции, необходимо указать начальные значения для параметров ядра.

Дополнительные сведения о функциях ядра см. в разделе Параметры функции Kernel (Covariance).

Пример: 'KernelParameters',theta

Типы данных: double

Метод вычисления межточечных расстояний для оценки встроенных функций ядра, определяемый как разделенная запятыми пара, состоящая из 'DistanceMethod' и либо 'fast' или 'accurate'. fitrgp вычисляет (x − y) 2 как x2 + y2 − 2 * x * y при выбореfast и как (x − y) 2 при выборе accurate вариант.

Пример: 'DistanceMethod','accurate'

Выбор активного набора

свернуть все

Наблюдения в активном наборе, указанном как разделенная запятыми пара, состоящая из 'ActiveSet' и вектор m-на-1 целых чисел в диапазоне от 1 до n (m ≤ n) или логический вектор длиной n по меньшей мере с одним true элемент. n - общее число наблюдений в данных обучения.

fitrgp использует наблюдения, указанные ActiveSet для обучения модели GPR. Активный набор не может иметь повторяющихся элементов.

Если вы поставляете ActiveSet, то:

  • fitrgp не использует ActiveSetSize и ActiveSetMethod.

  • Невозможно выполнить перекрестную проверку для этой модели.

Типы данных: double | logical

Размер активного набора для разреженных методов ('sd', 'sr', 'fic'), указанная как пара, разделенная запятыми, состоящая из 'ActiveSetSize' и целое число m, 1 ≤ m ≤ n, где n - число наблюдений.

Значение по умолчанию - min (1000, n), еслиFitMethod является 'sr' или 'fic'и мин (2000, n), в противном случае.

Пример: 'ActiveSetSize',100

Типы данных: double

Метод выбора активного набора, заданный как разделенная запятыми пара, состоящая из 'ActiveSetMethod' и одно из следующих.

МетодОписание
'random'Случайный выбор
'sgma'Разреженная жадная матричная аппроксимация
'entropy'Выбор на основе дифференциальной энтропии
'likelihood'Подмножество регрессоров логарифмического выбора на основе правдоподобия

Все активные методы выбора наборов (кроме 'random') требуют сохранения матрицы n-by-m, где m - размер активного множества, а n - количество наблюдений.

Пример: 'ActiveSetMethod','entropy'

Случайный размер набора поиска для жадного включения для выбора активного набора, указанного как пара, разделенная запятыми, состоящая из 'RandomSearchSetSize' и целочисленное значение.

Пример: 'RandomSearchSetSize',30

Типы данных: double

Относительный допуск для завершения выбора активного набора, указанного как пара, разделенная запятыми, состоящая из 'ToleranceActiveset' и положительное скалярное значение.

Пример: 'ToleranceActiveset',0.0002

Типы данных: double

Количество повторений для выбора чередующегося активного набора и оценки параметров при ActiveSetMethod не является 'random', указанная как пара, разделенная запятыми, состоящая из 'NumActiveSetRepeats' и целочисленное значение.

Пример: 'NumActiveSetRepeats',5

Типы данных: double

Прогноз

свернуть все

Метод, используемый для прогнозирования из модели гауссова процесса с учетом параметров, указанных как пара, разделенная запятыми, состоящая из 'PredictMethod' и одно из следующих.

МетодОписание
'exact'Точный метод регрессии гауссова процесса. По умолчанию, если n ≤ 10000.
'bcd'Снижение координат блока. По умолчанию, если n > 10000.
'sd'Подмножество аппроксимации точек данных.
'sr'Подмножество аппроксимации регрессоров.
'fic'Полностью независимое условное приближение.

Пример: 'PredictMethod','bcd'

Размер блока для метода снижения координат блока ('bcd'), указанная как пара, разделенная запятыми, состоящая из 'BlockSizeBCD' и целое число в диапазоне от 1 до n, где n - число наблюдений.

Пример: 'BlockSizeBCD',1500

Типы данных: double

Количество жадных выборок для метода снижения координат блока ('bcd'), указанная как пара, разделенная запятыми, состоящая из 'NumGreedyBCD' и целое число в диапазоне от 1 до BlockSizeBCD.

Пример: 'NumGreedyBCD',150

Типы данных: double

Относительный допуск по градиентной норме для метода снижения координат завершающего блока ('bcd') итерации, указанные как пара, разделенная запятыми, состоящая из 'ToleranceBCD' и положительный скаляр.

Пример: 'ToleranceBCD',0.002

Типы данных: double

Абсолютный допуск по размеру шага для метода снижения координат завершающего блока ('bcd') итерации, указанные как пара, разделенная запятыми, состоящая из 'StepToleranceBCD' и положительный скаляр.

Пример: 'StepToleranceBCD',0.002

Типы данных: double

Максимальное количество методов снижения координат блока ('bcd') итерации, указанные как пара, разделенная запятыми, состоящая из 'IterationLimitBCD' и целочисленное значение.

Пример: 'IterationLimitBCD',10000

Типы данных: double

Оптимизация

свернуть все

Оптимизатор для оценки параметров, указанный как пара, разделенная запятыми, состоящая из 'Optimizer' и одно из значений в этой таблице.

СтоимостьОписание
'quasinewton'Плотное, симметричное рангово-1-основанное квази-ньютоновское приближение к гессенскому
'lbfgs'Квазиньютоновское приближение на основе LBFGS к гессенскому
'fminsearch'Неограниченная нелинейная оптимизация с использованием метода симплексного поиска Lagarias et al. [5]
'fminunc'Неограниченная нелинейная оптимизация (требуется лицензия Optimization Toolbox™)
'fmincon'Ограниченная нелинейная оптимизация (требуется лицензия Optimization Toolbox)

Дополнительные сведения об оптимизаторах см. в разделе Алгоритмы.

Пример: 'Optimizer','fmincon'

Опции для оптимизатора, выбранного с помощью Optimizer аргумент пары имя-значение, указанный как пара, разделенная запятыми, состоящая из 'OptimizerOptions' и структура или объект, созданный optimset, statset('fitrgp'), или optimoptions.

ОптимизаторСоздание параметров оптимизатора с помощью
'fminsearch'optimset (структура)
'quasinewton' или 'lbfgs'statset('fitrgp') (структура)
'fminunc' или 'fmincon'optimoptions (объект)

Параметры по умолчанию зависят от типа оптимизатора.

Пример: 'OptimizerOptions',opt

Начальный размер шага, указанный как разделенная запятыми пара, состоящая из 'InitialStepSize' и действительный положительный скаляр или 'auto'.

'InitialStepSize' - приблизительное максимальное абсолютное значение первого шага оптимизации, когда оптимизатор 'quasinewton' или 'lbfgs'. Начальный размер шага может определять начальное гессеновское приближение во время оптимизации.

По умолчанию fitrgp не использует начальный размер шага для определения начального гессенского приближения. Чтобы использовать начальный размер шага, задайте значение для 'InitialStepSize' аргумент пары имя-значение или укажите 'InitialStepSize','auto' иметь fitrgp автоматически определить значение. Для получения дополнительной информации о 'auto', см. Алгоритмы.

Пример: 'InitialStepSize','auto'

Перекрестная проверка

свернуть все

Индикатор для перекрестной проверки, указанный как пара, разделенная запятыми, состоящая из 'CrossVal' и либо 'off' или 'on'. Если это так 'on', то fitrgp возвращает модель GPR, прошедшую перекрестную проверку с 10 складками.

Вы можете использовать один из KFold, Holdout, Leaveout или CVPartition аргументы пары «имя-значение» для изменения параметров перекрестной проверки по умолчанию. Одновременно можно использовать только одну из этих пар имя-значение.

В качестве альтернативы можно использовать crossval метод для модели.

Пример: 'CrossVal','on'

Случайное разбиение для стратифицированной k-кратной перекрестной проверки, указанной как пара, разделенная запятыми, состоящая из 'CVPartition' и cvpartition объект.

Пример: 'CVPartition',cvp использует случайный раздел, определенный cvp.

При указании CVPartition, то вы не можете указать Holdout, KFold, или Leaveout.

Доля данных, используемых для тестирования при проверке удержания, указанная как пара, разделенная запятыми, состоящая из 'Holdout' и скалярное значение в диапазоне от 0 до 1. При указании 'Holdout',p, затем программное обеспечение:
1. Случайным образом резервирует около p * 100% данных в качестве данных проверки и обучает модель, используя остальные данные
2. Хранение компактной обучаемой модели в cvgprMdl.Trained.

Пример: 'Holdout', 0.3 использует 30% данных для тестирования и 70% данных для обучения.

При указании Holdout, то вы не можете указать CVPartition, KFold, или Leaveout.

Типы данных: double

Количество сгибов для использования в модели GPR с перекрестной проверкой, указанной как пара, разделенная запятыми, состоящая из 'KFold' и положительное целое значение. KFold должно быть больше 1. При указании 'KFold',k затем программное обеспечение:
1. Случайным образом разбивает данные на k наборов.
2. Для каждого набора резервирует набор в качестве тестовых данных и обучает модель с использованием других k-1 наборов.
3. Хранит k компактных обученных моделей в ячейках массива ячеек k-by-1 в cvgprMdl.Trained.

Пример: 'KFold',5 использует 5 складок при перекрестной проверке. То есть для каждой складки использует эту складку в качестве тестовых данных и тренирует модель на оставшихся 4 складках.

При указании KFold, то вы не можете указать CVPartition, Holdout, или Leaveout.

Типы данных: double

Индикатор перекрестной проверки при отсутствии, указанный как пара, разделенная запятыми, состоящая из 'Leaveout' и либо 'off' или 'on'.

При указании 'Leaveout','on'затем для каждого из n наблюдений программное обеспечение:
1. Резервирует наблюдения в виде тестовых данных и обучает модель с использованием других n-1 наблюдений.
2. Хранение компактной обучаемой модели в ячейке в массиве ячеек n-by-1 cvgprMdl.Trained.

Пример: 'Leaveout','on'

При указании Leaveout, то вы не можете указать CVPartition, Holdout, или KFold.

Оптимизация гиперпараметров

свернуть все

Параметры для оптимизации, указанные как пара, разделенная запятыми, состоящая из 'OptimizeHyperparameters' и одно из следующих:

  • 'none' - Не оптимизировать.

  • 'auto' - Использование {'Sigma'}.

  • 'all' - Оптимизировать все подходящие параметры, эквивалентные{'BasisFunction','KernelFunction','KernelScale','Sigma','Standardize'}.

  • Строковый массив или массив ячеек допустимых имен параметров.

  • Вектор optimizableVariable объекты, обычно выходные данные hyperparameters.

Оптимизация пытается минимизировать потери при перекрестной проверке (ошибка) для fitrgp путем изменения параметров. Сведения о потере при перекрестной проверке (хотя и в другом контексте) см. в разделе Потеря классификации. Для управления типом перекрестной проверки и другими аспектами оптимизации используйте HyperparameterOptimizationOptions пара имя-значение.

Примечание

'OptimizeHyperparameters' значения переопределяют любые значения, заданные с помощью других аргументов пары «имя-значение». Например, настройка 'OptimizeHyperparameters' кому 'auto' вызывает 'auto' значения для применения.

Подходящие параметры для fitrgp являются:

  • BasisFunction — fitrgp поиск среди 'constant', 'none', 'linear', и 'pureQuadratic'.

  • KernelFunction — fitrgp поиск среди 'ardexponential', 'ardmatern32', 'ardmatern52', 'ardrationalquadratic', 'ardsquaredexponential', 'exponential', 'matern32', 'matern52', 'rationalquadratic', и 'squaredexponential'.

  • KernelScale — fitrgp использует KernelParameters для указания значения параметра масштаба ядра, которое поддерживается постоянным во время подгонки. В этом случае все входные размеры ограничены одним и тем же KernelScale значение. fitrgp поиск среди реальных значений в диапазоне [1e-3*MaxPredictorRange,MaxPredictorRange], где

    MaxPredictorRange = max(max(X) - min(X)).

    KernelScale не может быть оптимизирован ни для одного из ядер ARD.

  • Sigma — fitrgp поиск среди реальных значений в диапазоне [1e-4, max(1e-3,10*ResponseStd)], где

    ResponseStd = std(y).

    Внутри, fitrgp устанавливает ConstantSigma пара имя-значение к true таким образом, значение Sigma постоянна во время фитинга.

  • Standardize — fitrgp поиск среди true и false.

Установка параметров, не используемых по умолчанию, путем передачи вектора optimizableVariable объекты, не имеющие значений по умолчанию. Например,

load fisheriris
params = hyperparameters('fitrgp',meas,species);
params(1).Range = [1e-4,1e6];

Проход params как значение OptimizeHyperparameters.

По умолчанию итеративное отображение отображается в командной строке, а графики отображаются в соответствии с количеством гиперпараметров в оптимизации. Для оптимизации и графиков целевой функцией является log ( 1 + потери при перекрестной проверке) для регрессии и коэффициент неправильной классификации для классификации. Для управления итеративным отображением установите Verbose области 'HyperparameterOptimizationOptions' аргумент пары имя-значение. Для управления графиками установите ShowPlots области 'HyperparameterOptimizationOptions' аргумент пары имя-значение.

Пример см. в разделе Оптимизация регрессии GPR.

Пример: 'auto'

Опции оптимизации, указанные как разделенная запятыми пара, состоящая из 'HyperparameterOptimizationOptions' и структура. Этот аргумент изменяет эффект OptimizeHyperparameters аргумент пары имя-значение. Все поля в структуре являются необязательными.

Имя поляЦенностиДефолт
Optimizer

  • 'bayesopt' - использовать байесовскую оптимизацию. Внутренний вызов этого параметра bayesopt.

  • 'gridsearch' - Использовать поиск по сетке с NumGridDivisions значения для измерения.

  • 'randomsearch' - Случайный поиск среди MaxObjectiveEvaluations точки.

'gridsearch' ищет в случайном порядке, используя равномерную выборку без замены из сетки. После оптимизации можно получить таблицу в порядке сетки с помощью команды sortrows(Mdl.HyperparameterOptimizationResults).

'bayesopt'
AcquisitionFunctionName

  • 'expected-improvement-per-second-plus'

  • 'expected-improvement'

  • 'expected-improvement-plus'

  • 'expected-improvement-per-second'

  • 'lower-confidence-bound'

  • 'probability-of-improvement'

Функции приобретения, имена которых включают per-second не дают воспроизводимых результатов, поскольку оптимизация зависит от времени выполнения целевой функции. Функции приобретения, имена которых включают plus изменять их поведение при чрезмерной эксплуатации области. Для получения дополнительной информации см. Типы функций сбора данных.

'expected-improvement-per-second-plus'
MaxObjectiveEvaluationsМаксимальное количество оценок целевой функции.30 для 'bayesopt' или 'randomsearch'и вся сетка для 'gridsearch'
MaxTime

Ограничение по времени, указанное как положительный реал. Ограничение по времени в секундах, измеренное tic и toc. Время выполнения может превышать MaxTime потому что MaxTime не прерывает оценки функций.

Inf
NumGridDivisionsДля 'gridsearch', количество значений в каждом измерении. Значение может быть вектором положительных целых чисел, дающим количество значений для каждого измерения, или скаляром, который применяется ко всем измерениям. Это поле игнорируется для категориальных переменных.10
ShowPlotsЛогическое значение, указывающее, показывать ли графики. Если trueв этом поле отображается наилучшее значение целевой функции относительно номера итерации. Если имеется один или два параметра оптимизации, и если Optimizer является 'bayesopt', то ShowPlots также строит график модели целевой функции по параметрам.true
SaveIntermediateResultsЛогическое значение, указывающее, сохранять ли результаты при Optimizer является 'bayesopt'. Если true, это поле перезаписывает переменную рабочей области с именем 'BayesoptResults' на каждой итерации. Переменная является BayesianOptimization объект.false
Verbose

Отображение в командной строке.

  • 0 - Нет итеративного дисплея

  • 1 - Итеративный дисплей

  • 2 - Итеративный дисплей с дополнительной информацией

Для получения более подробной информации см. bayesopt Verbose аргумент пары имя-значение.

1
UseParallelЛогическое значение, указывающее, выполнять ли байесовскую оптимизацию параллельно, что требует Toolbox™ параллельных вычислений. Из-за непродуктивности параллельной синхронизации параллельная байесовская оптимизация не обязательно дает воспроизводимые результаты. Дополнительные сведения см. в разделе Параллельная байесовская оптимизация.false
Repartition

Логическое значение, указывающее, следует ли перераспределять перекрестную проверку при каждой итерации. Если falseоптимизатор использует один раздел для оптимизации.

true обычно дает наиболее надежные результаты, поскольку этот параметр учитывает секционирующий шум. Однако для хороших результатов, true требуется, по крайней мере, вдвое больше оценок функций.

false
Используйте не более одного из следующих трех имен полей.
CVPartitionA cvpartition объект, созданный cvpartition.'Kfold',5 если не указано какое-либо поле перекрестной проверки
HoldoutСкаляр в диапазоне (0,1) представляет собой удерживающую фракцию.
KfoldЦелое число больше 1.

Пример: 'HyperparameterOptimizationOptions',struct('MaxObjectiveEvaluations',60)

Типы данных: struct

Другое

свернуть все

Имена переменных предиктора, указанные как пара, разделенная запятыми, состоящая из 'PredictorNames' и строковый массив уникальных имен или массив ячеек уникальных векторов символов. Функциональные возможности 'PredictorNames' зависит от способа ввода данных обучения.

  • Если вы поставляете X и y, то вы можете использовать 'PredictorNames' дать переменные предиктора в X имена.

    • Порядок имен в PredictorNames должен соответствовать порядку столбцов X. То есть PredictorNames{1} является именем X(:,1), PredictorNames{2} является именем X(:,2)и так далее. Также, size(X,2) и numel(PredictorNames) должно быть равным.

    • По умолчанию PredictorNames является {'x1','x2',...}.

  • Если вы поставляете Tbl, то вы можете использовать 'PredictorNames' чтобы выбрать, какие переменные предиктора использовать в обучении. То есть fitrgp использует переменные предиктора в PredictorNames и ответ только на обучение.

    • PredictorNames должен быть подмножеством Tbl.Properties.VariableNames и не может включать имя переменной ответа.

    • По умолчанию PredictorNames содержит имена всех переменных предиктора.

    • Рекомендуется указывать предикторы для обучения с использованием одного из 'PredictorNames' или formula только.

Пример: 'PredictorNames',{'PedalLength','PedalWidth'}

Типы данных: string | cell

Имя переменной ответа, указанное как вектор символа или скаляр строки.

  • Если вы поставляете Y, то вы можете использовать 'ResponseName' для указания имени переменной ответа.

  • Если вы поставляете ResponseVarName или formula, то вы не можете использовать 'ResponseName'.

Пример: 'ResponseName','response'

Типы данных: char | string

Уровень детализации, указанный как разделенная запятыми пара, состоящая из 'Verbose' и одно из следующих.

  • 0 — fitrgp подавляет диагностические сообщения, связанные с выбором активного набора и снижением координат блока, но отображает сообщения, связанные с оценкой параметров, в зависимости от значения 'Display' в OptimizerOptions.

  • 1 — fitrgp отображает итеративные диагностические сообщения, связанные с оценкой параметров, выбором активного набора и снижением координат блока.

Пример: 'Verbose',1

Размер кэша в мегабайтах (МБ), указанный как разделенная запятыми пара, состоящая из 'CacheSize' и положительный скаляр. Размер кэша - это дополнительная память, доступная в дополнение к той, которая требуется для выбора фитинга и активного набора. fitrgp использование CacheSize кому:

  • Решите, следует ли кэшировать расстояния между точками при оценке параметров.

  • Решите, как следует вычислять векторные произведения матриц для метода снижения координат блока и для составления прогнозов.

Пример: 'CacheSize',2000

Типы данных: double

Выходные аргументы

свернуть все

Модель регрессии гауссова процесса, возвращенная как RegressionGP или RegressionPartitionedModel объект.

  • При перекрестной проверке, то есть при использовании одного из 'Crossval', 'KFold', 'Holdout', 'Leaveout', или 'CVPartition' пары имя-значение, затем gprMdl является RegressionPartitionedModel объект. Нельзя использовать RegressionPartitionedModel объект для составления прогнозов с использованием predict. Дополнительные сведения о методах и свойствах этого объекта см. в разделе RegressionPartitionedModel.

  • Если перекрестная проверка не выполняется, то gprMdl является RegressionGP объект. Этот объект можно использовать для прогнозов с помощью predict способ. Дополнительные сведения о методах и свойствах этого объекта см. в разделе RegressionGP.

Подробнее

свернуть все

Выбор активного набора и оценка параметров

Для подмножества данных, подмножества регрессоров или полностью независимых методов аппроксимации условного приближения (FitMethod равно 'sd', 'sr', или 'fic'), если вы не предоставляете активный аппарат, fitrgp выбирает активное множество и вычисляет оценки параметров в серии итераций.

В первом повторении программное обеспечение использует начальные значения параметров в векторе η0 = [β0, σ0, θ0], чтобы выбрать активный набор A1. Он максимизирует предельное логарифмическое правдоподобие GPR или его аппроксимацию, используя (0) в качестве начальных значений и A1 для вычисления новых оценок (1) параметров. Затем он вычисляет новый логарифмический L1 правдоподобия с помощью A1.

Во второй итерации программное обеспечение выбирает активный набор A2 используя значения параметров, указанные в (в). Затем, используя его в качестве начальных значений и A2, он максимизирует предельное логарифмическое правдоподобие GPR или его аппроксимацию, а также оценивает новые значения (2) параметров. Тогда используя η2 и A2, вычисляет новую стоимость вероятности регистрации L2.

В следующей таблице представлены итерации и вычисляемые значения для каждой итерации.

Номер итерацииАктивный наборВектор параметровЛогарифмическая вероятность
1A1η1L1
2A2η2L2
3A3η3L3
…………

Программное обеспечение выполняет аналогичные итерации для заданного числа повторов. Можно указать количество репликаций для выбора активного набора с помощью NumActiveSetRepeats аргумент пары имя-значение.

Совет

  • fitrgp принимает любую комбинацию методов подбора, прогнозирования и выбора активного набора. В некоторых случаях может оказаться невозможным вычислить стандартные отклонения прогнозируемых откликов, следовательно, интервалы прогнозирования. Посмотрите predict. И в некоторых случаях использование точного метода может быть дорогостоящим из-за размера данных обучения.

  • PredictorNames свойство сохраняет один элемент для каждого из исходных имен переменных предиктора. Например, если существует три предиктора, один из которых является категориальной переменной с тремя уровнями, PredictorNames представляет собой массив символьных векторов типа «1 на 3».

  • ExpandedPredictorNames свойство сохраняет один элемент для каждой из переменных предиктора, включая фиктивные переменные. Например, если существует три предиктора, один из которых является категориальной переменной с тремя уровнями, то ExpandedPredictorNames представляет собой массив символьных векторов 1 на 5 ячеек.

  • Аналогично, Beta свойство хранит один бета-коэффициент для каждого предиктора, включая фиктивные переменные.

  • X свойство сохраняет данные обучения в том виде, в каком они были первоначально введены. Он не включает фиктивные переменные.

  • Подход по умолчанию к инициализации гессенского приближения в fitrgp может быть медленным при использовании модели GPR с множеством параметров ядра, например, при использовании ядра ARD со множеством предикторов. В этом случае рассмотрите возможность указания 'auto' или значение начального размера шага.

    Можно задать 'Verbose',1 для отображения итеративных диагностических сообщений и начать обучение модели GPR с использованием оптимизатора LBFGS или квазиньютоновского оптимизатора по умолчанию fitrgp оптимизация. Если итеративные диагностические сообщения не отображаются через несколько секунд, возможно, что инициализация гессенского приближения занимает слишком много времени. В этом случае рекомендуется перезапустить обучение и использовать начальный размер шага для ускорения оптимизации.

  • После обучения модели можно создать код C/C + +, который предсказывает ответы на новые данные. Для создания кода C/C + + требуется Coder™ MATLAB. Дополнительные сведения см. в разделе Введение в создание кода.

Алгоритмы

  • Подбор модели GPR включает оценку следующих параметров модели на основе данных:

    • Ковариационная функция k (xi, xj 'start), параметризованная в терминах параметров ядра в векторе (см. Параметры функции ядра (ковариации))

    • Шумовая дисперсия,

    • Вектор коэффициентов фиксированных базисных функций, β

    Значение 'KernelParameters' аргумент пары «имя-значение» - вектор, состоящий из начальных значений для среднеквадратичного отклонения в сигнале, а также шкал характеристических длин («» factoric length «»). fitrgp функция использует эти значения для определения параметров ядра. Аналогично, 'Sigma' Аргумент пары «имя-значение» содержит начальное значение для среднеквадратичного отклонения λ шума.

  • Во время оптимизации, fitrgp создает вектор из неограниченных значений начальных параметров, используя начальные значения для среднеквадратического отклонения шума и параметров ядра.

  • fitrgp аналитически определяет явные базисные коэффициенты β, определенные 'Beta' аргумент пары "имя-значение", из оценочных значений ("" "" "" "" "" "" "" "" "" "" "" " Поэтому β не появляется в векторе, когда fitrgp инициализирует численную оптимизацию.

    Примечание

    При отсутствии оценки параметров для модели GPR fitrgp использует значение 'Beta' аргумент пары имя-значение и другие начальные значения параметров в качестве известных значений параметров GPR (см. Beta). Во всех остальных случаях значение 'Beta' аргумент оптимизируется аналитически из целевой функции.

  • Квазиньютоновский оптимизатор использует метод доверительной области с плотным, симметричным рангом-1 на основе (SR1), квазиньютоновское приближение к гессенскому, в то время как LBFGS оптимизатор использует стандартный метод поиска линий с ограниченной памятью Бройдена-Флетчера-Гольдфарба-Шанно (Lanno См. Нокедаль и Райт [6].

  • Если установить 'InitialStepSize' аргумент пары имя-значение для 'auto', fitrgp определяет начальный размер шага, ‖ s0‖∞, с помощью ‖ s0‖∞=0.5‖η0‖∞+0.1.

    s0 - начальный пошаговый вектор, а λ 0 - вектор неограниченных значений начальных параметров.

  • Во время оптимизации, fitrgp использует начальный размер шага, ‖ s0‖∞, следующим образом:

    Если вы используете 'Optimizer','quasinewton' при начальном размере шага тогда начальное гессенское приближение равно ‖ g0‖∞‖s0‖∞I.

    Если вы используете 'Optimizer','lbfgs' при начальном размере шага тогда начальное обратногессенское приближение равно ‖ s0‖∞‖g0‖∞I.

    g0 - начальный градиентный вектор, а I - единичная матрица.

    • Ссылки

    [1] Нэш, У. Джей, Т. Л. Селлерс, С. Р. Толбот, А. Дж. Коуторн и У. Б. Форд. "Популяционная биология Абалоне (вид Haliotis) в Тасмании. И. Блэклип Абалоне (Х. рубра) с Северного побережья и островов Бассова пролива ". Отдел морского рыболовства, Технический доклад № 48, 1994 год.

    [2] Во, С. «Расширение и сравнительный анализ каскадной корреляции: расширение каскадно-корреляционной архитектуры и сравнительный анализ искусственных нейронных сетей, находящихся под контролем Feed-Forward». Факультет компьютерных наук Тасманийского университета, 1995 год.

    [3] Лихман, M. UCI Machine Learning Repository, Ирвайн, Калифорния: Калифорнийский университет, Школа информации и компьютерных наук, 2013. http://archive.ics.uci.edu/ml.

    [4] Расмуссен, К. Э. и К. К. И. Уильямс. Гауссовы процессы машинного обучения. Пресс MIT. Кембридж, Массачусетс, 2006.

    [5] Лагариас, Дж. С., Дж. А. Ридс, М. Х. Райт и П. Э. Райт. «Свойства сходимости метода Nelder-Mead Simplex в малых размерах». Журнал оптимизации SIAM. Том 9, номер 1, 1998, стр. 112-147.

    [6] Nocedal, J. и С. Дж. Райт. Численная оптимизация, второе издание. Springer Series in Operations Research, Springer Verlag, 2006.

    Расширенные возможности

    См. также

    | |

    Темы

    Представлен в R2015b

    Документация по инструментам для статистического и машинного обучения

    Поддержка