Генераторы квазислучайных чисел (QRNG) производят высокооднородные выборки единичного гиперкуба. QRNG минимизируют расхождение между распределением генерируемых точек и распределением с равными пропорциями точек в каждом подкубе равномерного разбиения гиперкуба. В результате QRNG систематически заполняют «дыры» в любом начальном сегменте генерируемой квазиплановой последовательности.
В отличие от псевдослучайных последовательностей, описанных в Common Pseudorandom Number Generation Methods, квазислучайные последовательности проваливают многие статистические тесты на случайность. Приблизительная истинная случайность, однако, не является их целью. Квазислучайные последовательности стремятся равномерно заполнить пространство и сделать это таким образом, чтобы начальные сегменты аппроксимировали это поведение вплоть до заданной плотности.
Приложения QRNG включают в себя:
Интеграция Квази-Монте-Карло (QMC). Методы Монте-Карло часто используются для оценки сложных многомерных интегралов без решения в замкнутой форме. QMC использует квазислучайные последовательности для улучшения свойств сходимости этих методов.
Экспериментальные проекты наполнения космоса. Во многих экспериментальных установках проводить измерения при каждой установке коэффициента дорого или неосуществимо. Квазислучайные последовательности обеспечивают эффективную, равномерную выборку расчетного пространства.
Глобальная оптимизация. Алгоритмы оптимизации обычно находят локальный оптимум в окрестности начального значения. Используя квазислучайную последовательность начальных значений, ищет глобальную оптимальную равномерную выборку бассейнов притяжения всех локальных минимумов.
Представьте простую 1-D последовательность, которая производит целые числа от 1 до 10. Это базовая последовательность и первые три точки [1,2,3]:
![]()
Теперь посмотрите, как Scramble, Skip, и Leap работать вместе:
Scramble - Скремблирование перетасовывает точки одним из нескольких различных способов. В этом примере предположим, что скремблирование превращает последовательность в 1,3,5,7,9,2,4,6,8,10. Первые три очка сейчас [1,3,5]:
![]()
Skip - A Skip значение указывает количество исходных точек, которые следует игнорировать. В этом примере установите Skip значение 2. Последовательность теперь 5,7,9,2,4,6,8,10 и первые три пункта [5,7,9]:
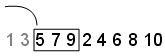
Leap - A Leap значение указывает количество точек, которые необходимо игнорировать для каждой взятой точки. Продолжение примера с помощью Skip значение 2, если установлено значение Leap 1, последовательность использует каждую другую точку. В этом примере последовательность теперь 5,9,4,8 и первые три пункта [5,9,4]:
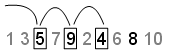
Функции Toolbox™ статистики и машинного обучения поддерживают следующие квазислучайные последовательности:
Последовательности Халтона. Произведено haltonset функция. Эти последовательности используют различные простые основания для образования последовательно более тонких однородных перегородок единичного интервала в каждом измерении.
Последовательности Соболь. Произведено sobolset функция. Эти последовательности используют базу из 2 для формирования последовательно более тонких однородных перегородок единичного интервала, а затем переупорядочивают координаты в каждом измерении.
Латинские последовательности гиперкубов. Произведено lhsdesign функция. Хотя эти последовательности не являются квазислучайными в смысле минимизации расхождений, они, тем не менее, дают разреженные однородные образцы, полезные в экспериментальных конструкциях.
Квазислучайные последовательности - это функции от положительных целых чисел до единичного гиперкуба. Для использования в приложении необходимо создать начальный набор точек последовательности. Наборы точек - это матрицы размера n-by-d, где n - количество точек, а d - размер дискретизируемого гиперкуба. Функции haltonset и sobolset создание наборов точек со свойствами указанной квазиплановой последовательности. Начальные сегменты наборов точек генерируются net способ haltonset и sobolset классы, но точки можно генерировать и обращаться к ним в более общем виде, используя индексирование в скобках.
Из-за того, как генерируются квазислучайные последовательности, они могут содержать нежелательные корреляции, особенно в их начальных сегментах, и особенно в более высоких измерениях. Для решения этой проблемы квазислучайные наборы точек часто пропускают, перепрыгивают или скремблируют значения в последовательности. haltonset и sobolset функции позволяют указать оба Skip и Leap свойство квазислучайной последовательности и scramble способ haltonset и sobolset классы позволяют применять различные методы скремблирования. Скремблирование уменьшает корреляции, а также улучшает однородность.
В этом примере показано, как использовать haltonset построить 2-й набор квазислучайной точки Холтона.
Создать haltonset объект p, что пропускает первые 1000 значений последовательности и затем сохраняет каждую 101-ю точку.
rng default % For reproducibility p = haltonset(2,'Skip',1e3,'Leap',1e2)
p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : none
Объект p инкапсулирует свойства указанной квазислучайной последовательности. Набор точек является конечным с длиной, определяемой Skip и Leap и по ограничениям на размер индексов набора точек.
Использовать scramble для применения скремблирования с обратным радиусом.
p = scramble(p,'RR2')p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : RR2
Использовать net для создания первых 500 точек.
X0 = net(p,500);
Это эквивалентно
X0 = p(1:500,:);
Значения набора точек X0 не генерируются и не сохраняются в памяти до тех пор, пока не будет получен доступ p использование net или индексирование в скобках.
Чтобы оценить природу квазислучайных чисел, создайте график рассеяния двух измерений в X0.
scatter(X0(:,1),X0(:,2),5,'r') axis square title('{\bf Quasi-Random Scatter}')

Сравните это с разбросом однородных псевдослучайных чисел, генерируемых rand функция.
X = rand(500,2); scatter(X(:,1),X(:,2),5,'b') axis square title('{\bf Uniform Random Scatter}')

Квазислучайное рассеяние выглядит более однородным, избегая скопления в псевдослучайном рассеянии.
В статистическом смысле квазислучайные числа слишком однородны, чтобы пройти традиционные тесты случайности. Например, тест Колмогорова-Смирнова, выполненный kstest, используется для оценки того, имеет ли набор точек равномерное случайное распределение. При многократном выполнении на однородных псевдослучайных образцах, например, генерируемых rand, тест дает равномерное распределение p-значений.
nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = rand(sampSize,1); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end histogram(PVALS,100) h = findobj(gca,'Type','patch'); xlabel('{\it p}-values') ylabel('Number of Tests')

Результаты совершенно различны, когда тест выполняется неоднократно на однородных квазиплановых выборках.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end histogram(PVALS,100) xlabel('{\it p}-values') ylabel('Number of Tests')

Малые p-значения ставят под сомнение нулевую гипотезу о том, что данные распределены равномерно. Если гипотеза верна, ожидается, что около 5% p-значений упадут ниже 0,05. Результаты удивительно последовательны в их неспособности оспорить гипотезу.
Квазислучайные потоки, производимые qrandstream функции используются для генерации последовательных квазиплановых выходных сигналов, а не наборов точек определенного размера. Потоки используются подобно pseudoRNGS, например rand, когда клиентским приложениям требуется источник квазислучайных чисел неопределенного размера, доступ к которым может осуществляться периодически. Свойства квазислучайного потока, такие как его тип (Халтон или Соболь), размерность, пропуск, скачок и скремблирование, устанавливаются при построении потока.
В реализации квазистрандовые потоки представляют собой, по существу, очень большие квазипландовые наборы точек, хотя доступ к ним осуществляется по-разному. Состояние квазислучайного потока - это скалярный индекс следующей точки, которая будет взята из потока. Используйте qrand способ qrandstream для создания точек из потока, начиная с текущего состояния. Используйте reset метод сброса состояния в 1. В отличие от наборов точек, потоки не поддерживают индексирование в скобках.
В этом примере показано, как генерировать выборки из квазипланового набора точек.
Использовать haltonset для создания квазипланового набора точек p, затем многократно приращение индекса в набор точек test для создания различных образцов.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end
Те же результаты получают с использованием qrandstream для построения квазислучайного потока q на основе набора точек p и предоставление потоку возможности заботиться о приращениях к индексу.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); q = qrandstream(p); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests X = qrand(q,sampSize); [h,pval] = kstest(X,[X,X]); PVALS(test) = pval; end