Функция Toolbox™ статистики и машинного обучения ecdf создает эмпирические функции кумулятивного риска, выжившего и кумулятивного распределения с помощью непараметрического метода Каплана-Мейера. Оценщик Каплана-Мейера для функции выжившего также называется оценщиком предела продукта.
Метод Каплана-Мейера использует данные о выживании, обобщенные в таблицах жизни. Таблицы жизненного цикла упорядочивают данные по возрастанию времени отказа, но не нужно вводить время отказа/выживания упорядоченным образом, чтобы использовать ecdf.
Жизненный стол обычно состоит из:
Время отказа
Число элементов, завершившихся сбоем за период времени
Количество элементов, подвергнутых цензуре за определенный период времени
Количество объектов риска в начале периода времени/времени
Число лиц, подвергающихся риску, представляет собой общее число выживших в начале каждого периода. Число в группе риска в начале первого периода - все люди в исследовании на всю жизнь. В начале каждого оставшегося периода число подверженных риску сокращается на количество отказов плюс лица, подвергшиеся цензуре в конце предыдущего периода.
Эта таблица жизни показывает фиктивные данные выживания. В начале первого времени отказа в зоне риска находятся семь объектов. В момент времени 4 три отказа. Так что в начале времени 7, есть четыре пункта риска. Только один сбой в момент времени 7, поэтому число в группе риска в начале времени 11 равно трем. Два отказа в момент времени 11, поэтому в начале времени 12 число в группе риска равно единице. Оставшаяся позиция не работает в момент времени 12.
| Время отказа (t) | Номер не выполнен | Число в зоне риска |
|---|---|---|
| 4 | 3 | 7 |
| 7 | 1 | 4 |
| 11 | 2 | 3 |
| 12 | 1 | 1 |
Функции риска, кумулятивного риска, выживания и кумулятивного распределения можно оценить с помощью таблиц жизненного цикла, как описано ниже.
Кумулятивная степень опасности (частота отказов)
Коэффициент опасности в каждом периоде - это количество отказов в данном периоде, деленное на число выживших особей в начале периода (число находящихся в группе риска).
| Время отказа (t) | Степень опасности (ч (т)) | Кумулятивный коэффициент опасности |
|---|---|---|
| 0 | 0 | 0 |
| t1 | d1/r1 | d1/r1 |
| t2 | d2/r2 | h (t1) + d2/r2 |
| ... | ... | ... |
| tn | дн/рн | h (tn - 1) + dn/rn |
Вероятность выживания
Для каждого периода вероятность выживания является результатом дополнения уровней опасности. Начальная вероятность выживания в начале первого периода времени равна 1. Если коэффициент опасности для каждого периода равен h (ti), то вероятность выжившего будет такой, как показано.
| Время (t) | Вероятность выживания (S (t)) |
|---|---|
| 0 | 1 |
| t1 | 1 * (1 - ч (t1)) |
| t2 | S (t1) * (1-h (t2)) |
| ... | ... |
| tn | S (tn-1) * (1-h (tn)) |
Функция совокупного распределения
Поскольку кумулятивная функция распределения (cdf) и функция выжившего являются дополнениями друг друга, можно найти cdf из таблиц жизни, используя F (t) = 1 - S (t).
Для смоделированных данных в первой таблице на этой странице можно вычислить кумулятивный коэффициент опасности, коэффициент выживаемости и кумулятивную функцию распределения следующим образом.
| t | Число неудачных (d) | Число в зоне риска (r) | Степень опасности | Вероятность выживания | Функция совокупного распределения |
|---|---|---|---|---|---|
| 4 | 3 | 7 | 3/7 | 1 – 3/7 = 4/7 = 0.5714 | 0.4286 |
| 7 | 1 | 4 | 1/4 | 4/7*(1 – 1/4) = 3/7 = .4286 | 0.5714 |
| 11 | 2 | 3 | 2/3 | 3/7*(1 – 2/3) = 1/7 = 0.1429 | 0.8571 |
| 12 | 1 | 1 | 1/1 | 1/7*(1 – 1) = 0 | 1 |
Эти скорости в этом примере основаны на дискретных временах отказа, и, следовательно, вычисления не обязательно следуют определению на основе производных в разделе Что такое анализ выживаемости?
Вот как можно ввести данные и вычислить эти показатели с помощью ecdf. Данные необязательно должны быть в порядке возрастания. Предположим, что время отказа хранится в массиве y.
y = [4 7 11 12];
freq = [3 1 2 1];
[f,x] = ecdf(y,'frequency',freq)f =
0
0.4286
0.5714
0.8571
1.0000
x =
4
4
7
11
12При цензуре данных таблица жизни может выглядеть следующим образом:
| Время (t) | Номер не выполнен (d) | Цензурирование | Число в зоне риска (r) | Степень опасности | Вероятность выживания | Функция совокупного распределения |
|---|---|---|---|---|---|---|
| 4 | 2 | 1 | 7 | 2/7 | 1 – 2/7 = 0.7143 | 0.2857 |
| 7 | 1 | 0 | 4 | 1/4 | 0.7143*(1 – 1/4) = 0.5357 | 0.4643 |
| 11 | 1 | 1 | 3 | 2/3 | 0.5357*(1 – 1/3) = 0.3571 | 0.6429 |
| 12 | 1 | 0 | 1 | 1/1 | 0.3571*(1 – 1) = 0 | 1.0000 |
В любой данный момент времени цензурированные элементы также учитываются в общей сумме числа подвергающихся риску, а формула коэффициента опасности основана на количестве провалившихся и общем количестве подвергающихся риску. При обновлении числа лиц, подвергающихся риску в начале каждого периода, общее число провалившихся и подвергшихся цензуре в предыдущем периоде уменьшается по сравнению с числом лиц, подвергшихся риску в начале этого периода.
При использовании ecdf, необходимо также ввести информацию о цензуре с помощью массива двоичных переменных. Введите 1 для данных, подвергнутых цензуре, и 0 для точного времени отказа.
y = [4 4 4 7 11 11 12];
cens = [0 1 0 0 1 0 0];
[f,x] = ecdf(y,'censoring',cens)f =
0
0.2857
0.4643
0.6429
1.0000
x =
4
4
7
11
12ecdfпо умолчанию создает значения кумулятивной функции распределения. Необходимо указать функцию выжившего или функцию опасности, используя необязательные аргументы пары имя-значение. Можно также построить график результатов следующим образом.
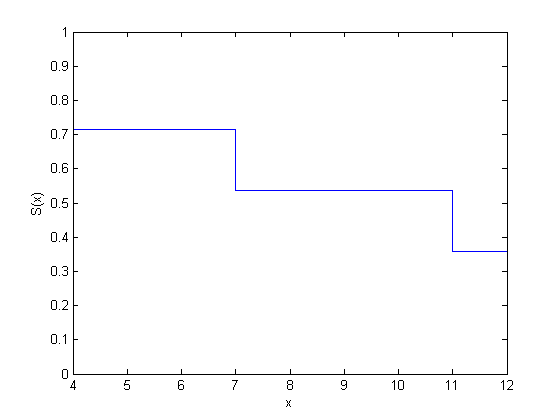
figure() ecdf(y,'censoring',cens,'function','survivor');
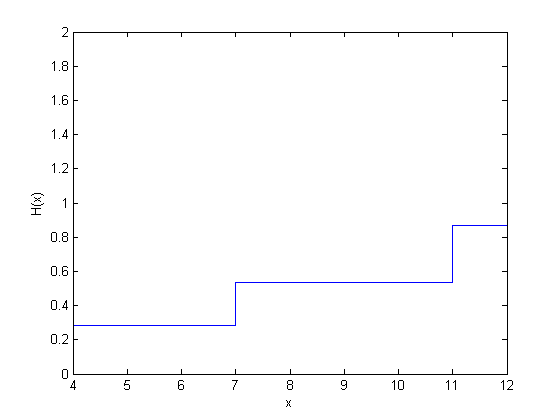
figure() ecdf(y,'censoring',cens,'function','cumulative hazard');
[1] Кокс, D. R. и Д. Оукс. Анализ данных о выживании. Лондон: Chapman & Hall, 1984.
[2] Беззаконие, J.F. Статистические модели и методы для данных о сроке службы. Хобокен, Нью-Джерси: Wiley-Interscience, 2002.
[3] Клейнбаум, Д. Г. и М. Кляйн. Анализ выживания. Статистика биологии и здравоохранения. 2-е издание. Спрингер, 2005.