Квадратичные поверхности отклика - это простые модели, которые обеспечивают максимум или минимум, не делая дополнительных предположений о форме отклика. Квадратичные модели могут быть откалиброваны с использованием полнофакторных конструкций с тремя или более уровнями для каждого фактора, но эти конструкции обычно требуют больше прогонов, чем необходимо для точной оценки параметров модели. В этом разделе рассматриваются конструкции для калибровки квадратичных моделей, которые являются гораздо более эффективными, используя три или пять уровней для каждого фактора, но не используя все комбинации уровней.
Центральные композитные конструкции (CCD), также известные как конструкции Бокса-Уилсона, подходят для калибровки полных квадратичных моделей. Существует три типа ПЗС - описанные, вписанные и лицевые - изображенные ниже:
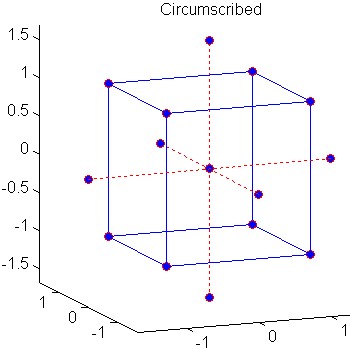
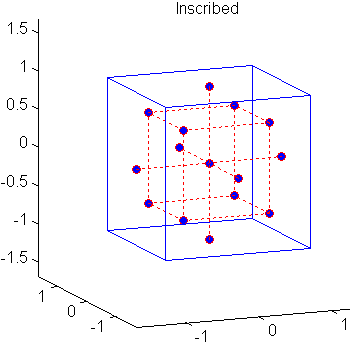
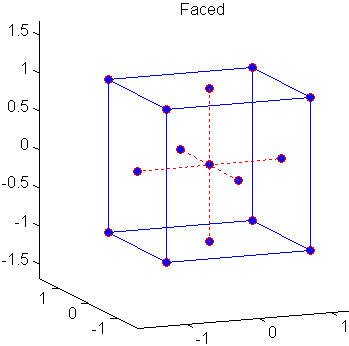
Каждая конструкция состоит из факториальной конструкции (углов куба) вместе с центрами и звездочками, которые позволяют оценить эффекты второго порядка. Для полной квадратичной модели с n факторами ПЗС имеют достаточно расчетных точек для оценки коэффициентов (n + 2) (n + 1 )/2 в полной квадратичной модели с n факторами.
Тип используемой ПЗС (положение факторной и звёздчатой точек) определяется количеством факторов и желаемыми свойствами конструкции. В следующей таблице приведены некоторые важные свойства. Конструкция может поворачиваться, если отклонение прогноза зависит только от расстояния точки конструкции от центра конструкции.
| Дизайн | Способный вращаться | Уровни коэффициентов | Использует точки вне ± 1 | Точность оценок |
|---|---|---|---|---|
| Описано (CCC) | Да | 5 | Да | Хорошо на всем проектном пространстве |
| Вписано (CCI) | Да | 5 | Нет | Преимущество над центральным подмножеством пространства для проектирования |
| Лицо (CCF) | Нет | 3 | Нет | Ярмарка по всему проектному пространству; плохо для чистых квадратичных коэффициентов |
Создание CCD с помощью функции ccdesign:
dCC = ccdesign(3,'type','circumscribed')
dCC =
-1.0000 -1.0000 -1.0000
-1.0000 -1.0000 1.0000
-1.0000 1.0000 -1.0000
-1.0000 1.0000 1.0000
1.0000 -1.0000 -1.0000
1.0000 -1.0000 1.0000
1.0000 1.0000 -1.0000
1.0000 1.0000 1.0000
-1.6818 0 0
1.6818 0 0
0 -1.6818 0
0 1.6818 0
0 0 -1.6818
0 0 1.6818
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0Повторные прогоны центральной точки позволяют получить более равномерную оценку дисперсии прогнозирования по всему пространству проектирования.
Как и конструкции, описанные в Central Composite Designs, конструкции Box-Behnken используются для калибровки полных квадратичных моделей. Конструкции Box-Behnken могут поворачиваться и для небольшого количества факторов (четыре или менее) требуют меньше прогонов, чем CCD. Избегая углов расчетного пространства, они позволяют экспериментаторам работать вокруг экстремальных комбинаций факторов. Однако, как и вписанная ПЗС, экстремумы затем плохо оцениваются.
Геометрия конструкции Box-Behnken представлена на следующем рисунке.
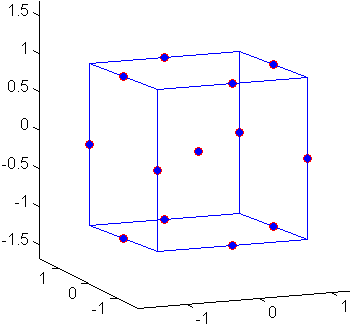
Точки проектирования находятся в середине кромок расчетного пространства и в центре и не содержат встроенной факторной конструкции.
Создать рамку (Generate Box) - проекты Behnken с функцией bbdesign:
dBB = bbdesign(3)
dBB =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0Повторные прогоны центральной точки также обеспечивают более равномерную оценку дисперсии прогнозирования по всему пространству проектирования.