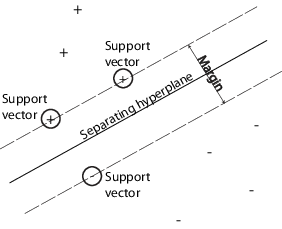
Можно использовать вспомогательную векторную машину (SVM), если данные имеют ровно два класса. SVM классифицирует данные, находя лучшую гиперплоскость, которая отделяет все точки данных одного класса от точек данных другого класса. Лучшая гиперплоскость для SVM означает гиперплоскость с наибольшим запасом между двумя классами. Поле означает максимальную ширину перекрытия, параллельного гиперплоскости, не имеющей внутренних точек данных.
Векторы поддержки являются точками данных, ближайшими к разделительной гиперплоскости; эти точки находятся на границе перекрытия. На следующем рисунке показаны эти определения с + указывающими точками данных типа 1 и - указывающими точками данных типа -1.
Математическая формулировка: Primal. Эта дискуссия следует за Хасти, Тибширани и Фридманом [1] и Кристианини и Шаве-Тейлором [2].
Данные для обучения представляют собой набор точек (векторов) xj вместе с их категориями yj. Для некоторого размера d, xj ∊ Rd и yj = ± 1. Уравнение гиперплоскости
=x′β+b=0
где β ∊ Rd и b - вещественное число.
Следующая задача определяет наилучшую разделяющую гиперплоскость (т.е. границу принятия решения). Найти β и b, которые минимизируют | | β | | такие, что для всех точек данных (xj, yj),
≥1.
Векторами поддержки являются xj на границе, те, для которых 1.
Для математического удобства задача обычно дается как эквивалентная задача минимизации ‖. Это квадратичная проблема программирования. Оптимальное b ^) позволяет классифицировать вектор z следующим образом:
f ^ (z)).
z) - оценка классификации и представляет расстояние z от границы принятия решения.
Математическая формулировка: двойственная. Для решения задачи двойного квадратичного программирования вычислительно проще. Чтобы получить двойственное, возьмем положительные множители Лагранжа αj, умноженные на каждое ограничение, и вычтем из целевой функции:
1),
где вы ищете стационарную точку ЛП над β и b. Установив градиент LP равным 0, вы получите
| (1) |
Подставляясь в ЛП, вы получаете двойную ЛД:
которую вы максимизируете над αj ≥ 0. В общем, многие αj равны 0 на максимуме. Ненулевое αj в решении двойной задачи определяет гиперплоскость, как видно в уравнении 1, которое дает β как сумму αjyjxj. Точки данных xj, соответствующие ненулевым αj, являются векторами поддержки.
Производная LD относительно ненулевого αj равна 0 при оптимуме. Это дает
= 0.
В частности, это дает значение b в растворе, принимая любой j с ненулевым αj.
Двойник является стандартной проблемой квадратичного программирования. Например, Toolbox™ «Оптимизация» quadprogРешатель (Панель инструментов оптимизации) решает проблему такого типа.
Возможно, данные не позволяют использовать разделяющую гиперплоскость. В этом случае SVM может использовать мягкое поле, означающее гиперплоскость, разделяющую многие, но не все точки данных.
Существуют две стандартные рецептуры мягких краев. И то, и другое включает в себя добавление переменных проволочек («slack variables»), и штрафного параметра C.
Проблема L1-norm заключается в следующем:
12β′β+C∑jξj)
такой, что
≥1−ξjξj≥0.
В L1-norm в качестве слабых переменных вместо их квадратов называется использование, например, Три опции решателя SMO, ISDA, и L1QP из fitcsvm минимизировать проблему L1-norm.
Проблема L2-norm заключается в следующем:
12β′β+C∑jξj2)
с теми же ограничениями.
В этих составах можно видеть, что увеличение C придает больший вес переменным «slack», что означает попытки оптимизации сделать более строгое разделение между классами. Эквивалентно, снижение C до 0 делает неправильную классификацию менее важной.
Математическая формулировка: двойственная. Для упрощения расчетов рассмотрите L1 двойную проблему в этой мягкой маржинальной формулировке. При использовании множителей Лагранжа (lagrange multipliates мкj) функция минимизации для L1-norm задачи состоит в следующем:
−∑jμjξj,
где вы ищете стационарную точку LP над β, b и положительной Установив градиент LP равным 0, вы получите
Эти уравнения приводят непосредственно к двойной формулировке:
с учетом ограничений
Конечный набор неравенств, 0 ≤ αj ≤ C, показывает, почему C иногда называют ограничением поля. C сохраняет допустимые значения множителей Лагранжа αj в «коробке», ограниченной области.
Уравнение градиента для b дает решение b в терминах множества ненулевых αj, которые соответствуют векторам поддержки.
Вы можете написать и решить двойственную проблему L2-norm аналогичным образом. Подробнее см. Christianini и Shawe-Taylor [2], глава 6.
fitcsvm Реализация. Обе двойные проблемы с мягкими полями являются проблемами с квадратичным программированием. Внутри, fitcsvm имеет несколько различных алгоритмов решения задач.
Для одноклассной или двоичной классификации, если в данных не задана доля ожидаемых отклонений (см. OutlierFraction), то решателем по умолчанию является Последовательная минимальная оптимизация (SMO). SMO минимизирует проблему одной нормы с помощью ряда двухточечных минимизаций. Во время оптимизации SMO соблюдает линейных ограничений
Если для двоичной классификации задана доля ожидаемых отклонений в данных, то решателем по умолчанию является итерационный алгоритм одиночных данных. Как и SMO, ISDA решает проблему одной нормы. В отличие от SMO, ISDA минимизируется серией на одноточечных минимизациях, не соблюдает линейное ограничение и не включает явно термин смещения в модель. Для получения дополнительной информации о ISDA см. [4].
Для одноклассной или двоичной классификации и при наличии лицензии Optimization Toolbox можно использовать quadprog(Панель инструментов оптимизации) для решения задачи «одна норма». quadprog использует много памяти, но решает квадратичные программы с высокой степенью точности. Дополнительные сведения см. в разделе Определение квадратного программирования (панель инструментов оптимизации).
Некоторые проблемы бинарной классификации не имеют простой гиперплоскости в качестве полезного критерия разделения. Для этих проблем существует вариант математического подхода, который сохраняет почти всю простоту гиперплоскости разделения SVM.
Этот подход использует эти результаты теории воспроизведения ядер:
Существует класс функций G (x1, x2) со следующим свойством. Существует линейное пространство S и функция, отображающая x на S так, что
G (x1, x2) = <
Скалярное произведение происходит в пространстве S.
Этот класс функций включает в себя:
Полиномы: Для некоторых положительных целое р,
G (x1, x2) = (1 + x1′x2) p.
Радиальная базисная функция (гауссова):
G (x1, x2) = exp (- ∥x1-x2) ∥2).
Многослойный перцептрон или сигмоид (нейронная сеть): для положительного числа p1 и отрицательного числа p2,
G (x1, x2) = tanh (p1x1′x2 + p2).
Примечание
Не каждый набор p1 и p2 дает действительное воспроизводящее ядро.
fitcsvm не поддерживает сигмоидальное ядро. Вместо этого можно определить sigmoid ядро и указать его с помощью 'KernelFunction' аргумент пары имя-значение. Дополнительные сведения см. в разделе Подготовка классификатора SVM с использованием пользовательского ядра.
Математический подход с использованием ядер опирается на вычислительный метод гиперплоскостей. Все вычисления для классификации гиперплоскостей используют не более чем точечные произведения. Поэтому нелинейные ядра могут использовать идентичные вычисления и алгоритмы решения, а также получать нелинейные классификаторы. Получившиеся классификаторы являются гиперповерхностями в некотором пространстве S, но пространство S не нужно идентифицировать или исследовать.
Как и в случае любой контролируемой модели обучения, сначала необходимо обучить машину вектора поддержки, а затем выполнить перекрестную проверку классификатора. Используйте обученную машину для классификации (прогнозирования) новых данных. Кроме того, для получения удовлетворительной точности прогнозирования можно использовать различные функции ядра SVM, а также необходимо настроить параметры функций ядра.
Подготовка и, при необходимости, перекрестная проверка классификатора SVM с использованием fitcsvm. Наиболее распространенный синтаксис:
SVMModel = fitcsvm(X,Y,'KernelFunction','rbf',...
'Standardize',true,'ClassNames',{'negClass','posClass'});Входными данными являются:
X - Матрица данных предиктора, где каждая строка является одним наблюдением, а каждый столбец является одним предиктором.
Y - Массив меток класса с каждой строкой, соответствующей значению соответствующей строки в X. Y может быть категориальным, символьным или строковым массивом, логическим или числовым вектором или массивом ячеек символьных векторов.
KernelFunction - Значение по умолчанию: 'linear' для двухклассного обучения, которое разделяет данные на гиперплоскость. Стоимость 'gaussian' (или 'rbf') является значением по умолчанию для одноклассного обучения и определяет использование ядра гауссова (или радиальной базовой функции). Важным шагом для успешной подготовки классификатора SVM является выбор соответствующей функции ядра.
Standardize - Флаг, указывающий, должно ли программное обеспечение стандартизировать предикторы перед обучением классификатора.
ClassNames - различает отрицательные и положительные классы или указывает, какие классы следует включить в данные. Отрицательный класс является первым элементом (или строкой символьного массива), например, 'negClass'и положительный класс является вторым элементом (или строкой символьного массива), например, 'posClass'. ClassNames должен быть того же типа данных, что и Y. Рекомендуется указывать имена классов, особенно при сравнении производительности различных классификаторов.
Полученная обученная модель (SVMModel) содержит оптимизированные параметры из алгоритма SVM, позволяющие классифицировать новые данные.
Для получения дополнительной информации о парах «имя-значение», которые можно использовать для управления обучением, см. fitcsvm справочная страница.
Классифицировать новые данные с помощью predict. Синтаксис для классификации новых данных с использованием обученного классификатора SVM (SVMModelявляется:
[label,score] = predict(SVMModel,newX);
Результирующий вектор, label, представляет классификацию каждой строки в X. score является матрицей мягких баллов n-на-2. Каждая строка соответствует строке в X, что является новым наблюдением. Первый столбец содержит оценки для наблюдений, классифицируемых в отрицательном классе, а второй столбец содержит оценки, классифицируемые в положительном классе.
Чтобы оценить апостериорные вероятности, а не баллы, сначала сдайте обученный классификатор SVM (SVMModelКому fitPosterior, которая соответствует функции преобразования «оценка-задняя вероятность». Синтаксис:
ScoreSVMModel = fitPosterior(SVMModel,X,Y);
Собственность ScoreTransform классификатора ScoreSVMModel содержит оптимальную функцию преобразования. Проход ScoreSVMModel кому predict. Вместо того, чтобы возвращать баллы, аргумент вывода score содержит апостериорные вероятности наблюдения, классифицируемого в отрицательном (столбец 1 из score) или положительным (столбец 2 из score) класс.
Используйте 'OptimizeHyperparameters' аргумент пары имя-значение fitcsvm для поиска значений параметров, которые минимизируют потери при перекрестной проверке. Допустимые параметры: 'BoxConstraint', 'KernelFunction', 'KernelScale', 'PolynomialOrder', и 'Standardize'. Пример см. в разделе Оптимизация посадки классификатора SVM с помощью байесовской оптимизации. Кроме того, можно использовать bayesopt , как показано в разделе Оптимизация кросс-проверенного классификатора SVM с использованием байесопта. bayesopt функция позволяет более гибко настраивать оптимизацию. Вы можете использовать bayesopt для оптимизации любых параметров, включая параметры, которые нельзя оптимизировать при использовании fitcsvm функция.
Можно также попробовать настроить параметры классификатора вручную в соответствии со следующей схемой:
Передача данных в fitcsvmи задайте аргумент пара имя-значение 'KernelScale','auto'. Предположим, что обучаемая модель SVM называется SVMModel. Программа использует эвристическую процедуру для выбора масштаба ядра. Эвристическая процедура использует субдискретизацию. Поэтому для воспроизведения результатов установите начальное число случайного числа, используя rng перед обучением классификатора.
Перекрестная проверка классификатора путем его передачи crossval. По умолчанию программное обеспечение выполняет 10-кратную перекрестную проверку.
Передача перекрестно проверенной модели SVM в kfoldLoss для оценки и сохранения ошибки классификации.
Перепрофилировать классификатор SVM, но скорректировать 'KernelScale' и 'BoxConstraint' аргументы пары имя-значение.
BoxConstraint - Одна из стратегий состоит в том, чтобы попробовать геометрическую последовательность параметра ограничения поля. Например, возьмите 11 значений, из 1e-5 кому 1e5 в 10 раз. Увеличение BoxConstraint может уменьшить число векторов поддержки, но также может увеличить время обучения.
KernelScale - Одна стратегия состоит в том, чтобы попробовать геометрическую последовательность параметра RBF sigma, масштабированного в исходном масштабе ядра. Для этого выполните следующие действия:
Получение исходной шкалы ядра, например, ks, используя точечную нотацию: ks = SVMModel.KernelParameters.Scale.
Использовать в качестве нового ядра масштабные коэффициенты оригинала. Например, умножить ks по 11 значениям 1e-5 кому 1e5, увеличиваясь в 10 раз.
Выберите модель, которая дает наименьшую ошибку классификации. Для повышения точности может потребоваться дальнейшее уточнение параметров. Начните с начальных параметров и выполните еще один шаг перекрестной проверки, на этот раз с коэффициентом 1,2.
В этом примере показано, как создать нелинейный классификатор с функцией ядра Гаусса. Сначала создайте один класс точек внутри диска блока в двух измерениях, а другой класс точек в кольцевом пространстве от радиуса 1 до радиуса 2. Затем генерирует классификатор на основе данных с ядром гауссовой радиальной базовой функции. Линейный классификатор по умолчанию явно непригоден для этой задачи, так как модель является круговой симметричной. Задайте для параметра ограничения поля значение Inf чтобы сделать строгую классификацию, что означает отсутствие ошибочной классификации обучающих баллов. Другие функции ядра могут не работать с этим строгим ограничением поля, поскольку они не могут обеспечить строгую классификацию. Даже если классификатор rbf может разделять классы, результат может быть переучен.
Создайте 100 точек, равномерно распределенных на диске устройства. Для этого создайте радиус r в виде квадратного корня однородной случайной величины, сформируйте угол t равномерно в (0, ) и поставьте точку в (r cos (t), r sin (t)).
rng(1); % For reproducibility r = sqrt(rand(100,1)); % Radius t = 2*pi*rand(100,1); % Angle data1 = [r.*cos(t), r.*sin(t)]; % Points
Создать 100 точек, равномерно распределенных в кольцевом пространстве. Радиус снова пропорционален квадратному корню, на этот раз квадратному корню равномерного распределения от 1 до 4.
r2 = sqrt(3*rand(100,1)+1); % Radius t2 = 2*pi*rand(100,1); % Angle data2 = [r2.*cos(t2), r2.*sin(t2)]; % points
Постройте график точек и постройте график окружностей радиусов 1 и 2 для сравнения.
figure; plot(data1(:,1),data1(:,2),'r.','MarkerSize',15) hold on plot(data2(:,1),data2(:,2),'b.','MarkerSize',15) ezpolar(@(x)1);ezpolar(@(x)2); axis equal hold off

Поместите данные в одну матрицу и создайте вектор классификаций.
data3 = [data1;data2]; theclass = ones(200,1); theclass(1:100) = -1;
Обучение классификатора SVM с помощью KernelFunction установить в значение 'rbf' и BoxConstraint установить в значение Inf. Постройте график границы решения и отметьте векторы поддержки.
%Train the SVM Classifier cl = fitcsvm(data3,theclass,'KernelFunction','rbf',... 'BoxConstraint',Inf,'ClassNames',[-1,1]); % Predict scores over the grid d = 0.02; [x1Grid,x2Grid] = meshgrid(min(data3(:,1)):d:max(data3(:,1)),... min(data3(:,2)):d:max(data3(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; [~,scores] = predict(cl,xGrid); % Plot the data and the decision boundary figure; h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,'rb','.'); hold on ezpolar(@(x)1); h(3) = plot(data3(cl.IsSupportVector,1),data3(cl.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'}); axis equal hold off

fitcsvm генерирует классификатор, близкий к окружности радиуса 1. Разница обусловлена случайными данными обучения.
Обучение с параметрами по умолчанию делает более близкой к круговой границу классификации, но ошибочно классифицирует некоторые данные обучения. Кроме того, значение по умолчанию BoxConstraint является 1и, следовательно, существует больше векторов поддержки.
cl2 = fitcsvm(data3,theclass,'KernelFunction','rbf'); [~,scores2] = predict(cl2,xGrid); figure; h(1:2) = gscatter(data3(:,1),data3(:,2),theclass,'rb','.'); hold on ezpolar(@(x)1); h(3) = plot(data3(cl2.IsSupportVector,1),data3(cl2.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'}); axis equal hold off

В этом примере показано, как использовать пользовательскую функцию ядра, например sigmoid kernel, для обучения классификаторов SVM и настройки параметров пользовательской функции ядра.
Создайте случайный набор точек в пределах единичной окружности. Метка указывает в первом и третьем квадрантах как принадлежащие положительному классу, а во втором и четвертом квадрантах - отрицательному классу.
rng(1); % For reproducibility n = 100; % Number of points per quadrant r1 = sqrt(rand(2*n,1)); % Random radii t1 = [pi/2*rand(n,1); (pi/2*rand(n,1)+pi)]; % Random angles for Q1 and Q3 X1 = [r1.*cos(t1) r1.*sin(t1)]; % Polar-to-Cartesian conversion r2 = sqrt(rand(2*n,1)); t2 = [pi/2*rand(n,1)+pi/2; (pi/2*rand(n,1)-pi/2)]; % Random angles for Q2 and Q4 X2 = [r2.*cos(t2) r2.*sin(t2)]; X = [X1; X2]; % Predictors Y = ones(4*n,1); Y(2*n + 1:end) = -1; % Labels
Постройте график данных.
figure;
gscatter(X(:,1),X(:,2),Y);
title('Scatter Diagram of Simulated Data')

Запишите функцию, которая принимает две матрицы в пространстве элементов в качестве входных данных и преобразует их в матрицу Gram с помощью сигмоидного ядра.
function G = mysigmoid(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 1; c = -1; G = tanh(gamma*U*V' + c); end
Сохранить этот код как файл с именем mysigmoid на пути MATLAB ®.
Обучение классификатора SVM с помощью функции sigmoid kernel. Рекомендуется стандартизировать данные.
Mdl1 = fitcsvm(X,Y,'KernelFunction','mysigmoid','Standardize',true);
Mdl1 является ClassificationSVM классификатор, содержащий оценочные параметры.
Постройте график данных и определите векторы поддержки и границу принятия решения.
% Compute the scores over a grid d = 0.02; % Step size of the grid [x1Grid,x2Grid] = meshgrid(min(X(:,1)):d:max(X(:,1)),... min(X(:,2)):d:max(X(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; % The grid [~,scores1] = predict(Mdl1,xGrid); % The scores figure; h(1:2) = gscatter(X(:,1),X(:,2),Y); hold on h(3) = plot(X(Mdl1.IsSupportVector,1),... X(Mdl1.IsSupportVector,2),'ko','MarkerSize',10); % Support vectors contour(x1Grid,x2Grid,reshape(scores1(:,2),size(x1Grid)),[0 0],'k'); % Decision boundary title('Scatter Diagram with the Decision Boundary') legend({'-1','1','Support Vectors'},'Location','Best'); hold off

Можно настроить параметры ядра, чтобы улучшить форму границы принятия решения. Это также может снизить коэффициент неправильной классификации внутри выборки, но сначала следует определить коэффициент неправильной классификации вне выборки.
Определите частоту неправильной классификации из выборки, используя 10-кратную перекрестную проверку.
CVMdl1 = crossval(Mdl1); misclass1 = kfoldLoss(CVMdl1); misclass1
misclass1 =
0.1350
Степень неправильной классификации вне выборки составляет 13,5%.
Записать другую сигмоидальную функцию, но Задать gamma = 0.5;.
function G = mysigmoid2(U,V) % Sigmoid kernel function with slope gamma and intercept c gamma = 0.5; c = -1; G = tanh(gamma*U*V' + c); end
Сохранить этот код как файл с именем mysigmoid2 на пути MATLAB ®.
Обучить другой классификатор SVM с помощью скорректированного сигмоидного ядра. Постройте график данных и области принятия решения и определите степень неправильной классификации из выборки.
Mdl2 = fitcsvm(X,Y,'KernelFunction','mysigmoid2','Standardize',true); [~,scores2] = predict(Mdl2,xGrid); figure; h(1:2) = gscatter(X(:,1),X(:,2),Y); hold on h(3) = plot(X(Mdl2.IsSupportVector,1),... X(Mdl2.IsSupportVector,2),'ko','MarkerSize',10); title('Scatter Diagram with the Decision Boundary') contour(x1Grid,x2Grid,reshape(scores2(:,2),size(x1Grid)),[0 0],'k'); legend({'-1','1','Support Vectors'},'Location','Best'); hold off CVMdl2 = crossval(Mdl2); misclass2 = kfoldLoss(CVMdl2); misclass2
misclass2 =
0.0450

После корректировки сигмоидного наклона новая граница принятия решения, по-видимому, обеспечивает лучшую подгонку внутри выборки, а ставка перекрестной проверки сокращается более чем на 66%.
В этом примере показано, как оптимизировать классификацию SVM с помощью fitcsvm функции и OptimizeHyperparameters пара имя-значение. Классификация работает на местах точек из гауссовой модели смеси. В «Элементах статистического обучения» Hastie, Tibshirani и Friedman (2009) на странице 17 описывается модель. Модель начинается с генерации 10 базовых точек для «зеленого» класса, распределенного как 2-D независимые нормали со средним значением (1,0) и единичной дисперсией. Он также генерирует 10 базовых точек для «красного» класса, распределенного как 2-D независимые нормали со средним значением (0,1) и единичной дисперсией. Для каждого класса (зеленого и красного) создайте 100 случайных точек следующим образом:
Выберите базовую точку m соответствующего цвета равномерно случайным образом.
Создайте независимую случайную точку с 2-D нормальным распределением со средним m и дисперсией I/5, где I - единичная матрица 2 на 2. В этом примере используйте I/50 дисперсии, чтобы более четко показать преимущество оптимизации.
Создание точек и классификатора
Создайте 10 базовых точек для каждого класса.
rng default % For reproducibility grnpop = mvnrnd([1,0],eye(2),10); redpop = mvnrnd([0,1],eye(2),10);
Просмотрите базовые точки.
plot(grnpop(:,1),grnpop(:,2),'go') hold on plot(redpop(:,1),redpop(:,2),'ro') hold off

Поскольку некоторые красные базовые точки близки к зеленым базовым точкам, может быть трудно классифицировать точки данных только на основе местоположения.
Создайте 100 точек данных каждого класса.
redpts = zeros(100,2);grnpts = redpts; for i = 1:100 grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02); redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02); end
Просмотр точек данных.
figure plot(grnpts(:,1),grnpts(:,2),'go') hold on plot(redpts(:,1),redpts(:,2),'ro') hold off

Подготовка данных для классификации
Поместите данные в одну матрицу и создайте вектор grp маркирует класс каждой точки.
cdata = [grnpts;redpts];
grp = ones(200,1);
% Green label 1, red label -1
grp(101:200) = -1;Подготовка перекрестной проверки
Настройте раздел для перекрестной проверки. На этом шаге фиксируются наборы каналов и тестов, используемые при оптимизации на каждом шаге.
c = cvpartition(200,'KFold',10);Оптимизация посадки
Чтобы найти хорошую подгонку, то есть с низкой потерей перекрестной проверки, задайте опции для использования байесовской оптимизации. Использовать тот же раздел перекрестной проверки c во всех оптимизациях.
Для воспроизводимости используйте 'expected-improvement-plus' функция приобретения.
opts = struct('Optimizer','bayesopt','ShowPlots',true,'CVPartition',c,... 'AcquisitionFunctionName','expected-improvement-plus'); svmmod = fitcsvm(cdata,grp,'KernelFunction','rbf',... 'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',opts)
|=====================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | | | result | | runtime | (observed) | (estim.) | | | |=====================================================================================================| | 1 | Best | 0.345 | 0.20756 | 0.345 | 0.345 | 0.00474 | 306.44 | | 2 | Best | 0.115 | 0.14872 | 0.115 | 0.12678 | 430.31 | 1.4864 | | 3 | Accept | 0.52 | 0.12556 | 0.115 | 0.1152 | 0.028415 | 0.014369 | | 4 | Accept | 0.61 | 0.16264 | 0.115 | 0.11504 | 133.94 | 0.0031427 | | 5 | Accept | 0.34 | 0.14384 | 0.115 | 0.11504 | 0.010993 | 5.7742 | | 6 | Best | 0.085 | 0.15049 | 0.085 | 0.085039 | 885.63 | 0.68403 | | 7 | Accept | 0.105 | 0.12919 | 0.085 | 0.085428 | 0.3057 | 0.58118 | | 8 | Accept | 0.21 | 0.15841 | 0.085 | 0.09566 | 0.16044 | 0.91824 | | 9 | Accept | 0.085 | 0.18577 | 0.085 | 0.08725 | 972.19 | 0.46259 | | 10 | Accept | 0.1 | 0.1428 | 0.085 | 0.090952 | 990.29 | 0.491 | | 11 | Best | 0.08 | 0.14182 | 0.08 | 0.079362 | 2.5195 | 0.291 | | 12 | Accept | 0.09 | 0.12232 | 0.08 | 0.08402 | 14.338 | 0.44386 | | 13 | Accept | 0.1 | 0.13074 | 0.08 | 0.08508 | 0.0022577 | 0.23803 | | 14 | Accept | 0.11 | 0.15858 | 0.08 | 0.087378 | 0.2115 | 0.32109 | | 15 | Best | 0.07 | 0.15241 | 0.07 | 0.081507 | 910.2 | 0.25218 | | 16 | Best | 0.065 | 0.15047 | 0.065 | 0.072457 | 953.22 | 0.26253 | | 17 | Accept | 0.075 | 0.15512 | 0.065 | 0.072554 | 998.74 | 0.23087 | | 18 | Accept | 0.295 | 0.14554 | 0.065 | 0.072647 | 996.18 | 44.626 | | 19 | Accept | 0.07 | 0.22102 | 0.065 | 0.06946 | 985.37 | 0.27389 | | 20 | Accept | 0.165 | 0.14178 | 0.065 | 0.071622 | 0.065103 | 0.13679 | |=====================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | BoxConstraint| KernelScale | | | result | | runtime | (observed) | (estim.) | | | |=====================================================================================================| | 21 | Accept | 0.345 | 0.12463 | 0.065 | 0.071764 | 971.7 | 999.01 | | 22 | Accept | 0.61 | 0.17579 | 0.065 | 0.071967 | 0.0010168 | 0.0010005 | | 23 | Accept | 0.345 | 0.1675 | 0.065 | 0.071959 | 0.0010674 | 999.18 | | 24 | Accept | 0.35 | 0.13478 | 0.065 | 0.071863 | 0.0010003 | 40.628 | | 25 | Accept | 0.24 | 0.23822 | 0.065 | 0.072124 | 996.55 | 10.423 | | 26 | Accept | 0.61 | 0.14478 | 0.065 | 0.072068 | 958.64 | 0.0010026 | | 27 | Accept | 0.47 | 0.13262 | 0.065 | 0.07218 | 993.69 | 0.029723 | | 28 | Accept | 0.3 | 0.15652 | 0.065 | 0.072291 | 993.15 | 170.01 | | 29 | Accept | 0.16 | 0.31079 | 0.065 | 0.072104 | 992.81 | 3.8594 | | 30 | Accept | 0.365 | 0.1375 | 0.065 | 0.072112 | 0.0010017 | 0.044287 |


__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 48.9578 seconds
Total objective function evaluation time: 4.7979
Best observed feasible point:
BoxConstraint KernelScale
_____________ ___________
953.22 0.26253
Observed objective function value = 0.065
Estimated objective function value = 0.073726
Function evaluation time = 0.15047
Best estimated feasible point (according to models):
BoxConstraint KernelScale
_____________ ___________
985.37 0.27389
Estimated objective function value = 0.072112
Estimated function evaluation time = 0.16248
svmmod =
ClassificationSVM
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [-1 1]
ScoreTransform: 'none'
NumObservations: 200
HyperparameterOptimizationResults: [1x1 BayesianOptimization]
Alpha: [77x1 double]
Bias: -0.2352
KernelParameters: [1x1 struct]
BoxConstraints: [200x1 double]
ConvergenceInfo: [1x1 struct]
IsSupportVector: [200x1 logical]
Solver: 'SMO'
Properties, Methods
Найдите потерю оптимизированной модели.
lossnew = kfoldLoss(fitcsvm(cdata,grp,'CVPartition',c,'KernelFunction','rbf',... 'BoxConstraint',svmmod.HyperparameterOptimizationResults.XAtMinObjective.BoxConstraint,... 'KernelScale',svmmod.HyperparameterOptimizationResults.XAtMinObjective.KernelScale))
lossnew = 0.0650
Эти потери аналогичны потерям, указанным в выходных данных оптимизации в разделе «Наблюдаемое значение целевой функции».
Визуализация оптимизированного классификатора.
d = 0.02; [x1Grid,x2Grid] = meshgrid(min(cdata(:,1)):d:max(cdata(:,1)),... min(cdata(:,2)):d:max(cdata(:,2))); xGrid = [x1Grid(:),x2Grid(:)]; [~,scores] = predict(svmmod,xGrid); figure; h = nan(3,1); % Preallocation h(1:2) = gscatter(cdata(:,1),cdata(:,2),grp,'rg','+*'); hold on h(3) = plot(cdata(svmmod.IsSupportVector,1),... cdata(svmmod.IsSupportVector,2),'ko'); contour(x1Grid,x2Grid,reshape(scores(:,2),size(x1Grid)),[0 0],'k'); legend(h,{'-1','+1','Support Vectors'},'Location','Southeast'); axis equal hold off

Этот пример показывает, как предсказать задние вероятности моделей SVM по сетке наблюдений, а затем построить график задних вероятностей по сетке. Построение задних вероятностей обнажает границы принятия решения.
Загрузите набор данных радужки Фишера. Обучите классификатор, используя длины и ширину лепестков, и удалите виды virginica из данных.
load fisheriris classKeep = ~strcmp(species,'virginica'); X = meas(classKeep,3:4); y = species(classKeep);
Обучение классификатора SVM с использованием данных. Рекомендуется указывать порядок классов.
SVMModel = fitcsvm(X,y,'ClassNames',{'setosa','versicolor'});
Оцените оптимальную функцию преобразования баллов.
rng(1); % For reproducibility
[SVMModel,ScoreParameters] = fitPosterior(SVMModel); Warning: Classes are perfectly separated. The optimal score-to-posterior transformation is a step function.
ScoreParameters
ScoreParameters = struct with fields:
Type: 'step'
LowerBound: -0.8431
UpperBound: 0.6897
PositiveClassProbability: 0.5000
Оптимальная функция преобразования баллов - это ступенчатая функция, поскольку классы являются разделяемыми. Области LowerBound и UpperBound из ScoreParameters укажите нижнюю и верхнюю конечные точки интервала оценок, соответствующих наблюдениям в гиперплоскостях, разделяющих классы (поле). Никакое наблюдение за обучением не подпадает под поле. Если новый балл находится в интервале, то программное обеспечение присваивает соответствующему наблюдению положительную апостериорную вероятность класса, то есть значение в PositiveClassProbability поле ScoreParameters.
Определите сетку значений в наблюдаемом предикторном пространстве. Предсказать апостериорные вероятности для каждого случая в сетке.
xMax = max(X); xMin = min(X); d = 0.01; [x1Grid,x2Grid] = meshgrid(xMin(1):d:xMax(1),xMin(2):d:xMax(2)); [~,PosteriorRegion] = predict(SVMModel,[x1Grid(:),x2Grid(:)]);
Постройте график области положительной апостериорной вероятности класса и тренировочных данных.
figure; contourf(x1Grid,x2Grid,... reshape(PosteriorRegion(:,2),size(x1Grid,1),size(x1Grid,2))); h = colorbar; h.Label.String = 'P({\it{versicolor}})'; h.YLabel.FontSize = 16; caxis([0 1]); colormap jet; hold on gscatter(X(:,1),X(:,2),y,'mc','.x',[15,10]); sv = X(SVMModel.IsSupportVector,:); plot(sv(:,1),sv(:,2),'yo','MarkerSize',15,'LineWidth',2); axis tight hold off

В двухклассном обучении, если классы разделены, то есть три области: одна, где наблюдения имеют положительную апостериорную вероятность класса 0, один, где он 1и другой, где это положительная вероятность предшествующего класса.
Этот пример показывает, как определить, какой квадрант изображения занимает форма, обучая модель выходных кодов с исправлением ошибок (ECOC), состоящую из линейных двоичных обучающихся SVM. Этот пример также иллюстрирует потребление дискового пространства моделями ECOC, в которых хранятся векторы поддержки, их метки и оцененные α-коэффициенты.
Создание набора данных
Случайным образом поместите круг с радиусом пять на изображение 50 на 50. Сделайте 5000 изображений. Создайте метку для каждого изображения, указывающую квадрант, который занимает окружность. Квадрант 1 находится в верхнем правом углу, квадрант 2 находится в верхнем левом углу, квадрант 3 находится в нижнем левом углу, квадрант 4 находится в нижнем правом углу. Предикторами являются интенсивности каждого пикселя.
d = 50; % Height and width of the images in pixels n = 5e4; % Sample size X = zeros(n,d^2); % Predictor matrix preallocation Y = zeros(n,1); % Label preallocation theta = 0:(1/d):(2*pi); r = 5; % Circle radius rng(1); % For reproducibility for j = 1:n figmat = zeros(d); % Empty image c = datasample((r + 1):(d - r - 1),2); % Random circle center x = r*cos(theta) + c(1); % Make the circle y = r*sin(theta) + c(2); idx = sub2ind([d d],round(y),round(x)); % Convert to linear indexing figmat(idx) = 1; % Draw the circle X(j,:) = figmat(:); % Store the data Y(j) = (c(2) >= floor(d/2)) + 2*(c(2) < floor(d/2)) + ... (c(1) < floor(d/2)) + ... 2*((c(1) >= floor(d/2)) & (c(2) < floor(d/2))); % Determine the quadrant end
Постройте график наблюдения.
figure imagesc(figmat) h = gca; h.YDir = 'normal'; title(sprintf('Quadrant %d',Y(end)))

Обучение модели ECOC
Используйте 25% -ную выборку и укажите учебные индексы и индексы выборки.
p = 0.25; CVP = cvpartition(Y,'Holdout',p); % Cross-validation data partition isIdx = training(CVP); % Training sample indices oosIdx = test(CVP); % Test sample indices
Создайте шаблон SVM, который определяет сохранение векторов поддержки двоичных учеников. Передать его и данные обучения в fitcecoc для обучения модели. Определите ошибку классификации учебных образцов.
t = templateSVM('SaveSupportVectors',true); MdlSV = fitcecoc(X(isIdx,:),Y(isIdx),'Learners',t); isLoss = resubLoss(MdlSV)
isLoss = 0
MdlSV является обученным ClassificationECOC мультиклассовая модель. Он хранит обучающие данные и векторы поддержки каждого двоичного ученика. Для больших наборов данных, например, в анализе изображений, модель может потреблять много памяти.
Определите объем дискового пространства, занимаемого моделью ECOC.
infoMdlSV = whos('MdlSV');
mbMdlSV = infoMdlSV.bytes/1.049e6mbMdlSV = 763.6150
Модель потребляет 763,6 МБ.
Повышение эффективности модели
Вы можете оценить производительность вне выборки. Можно также оценить, была ли модель заменена уплотненной моделью, которая не содержит векторов поддержки, связанных с ними параметров и данных обучения.
Отбросьте векторы поддержки и связанные параметры из обученной модели ECOC. Затем удалите учебные данные из полученной модели с помощью compact.
Mdl = discardSupportVectors(MdlSV); CMdl = compact(Mdl); info = whos('Mdl','CMdl'); [bytesCMdl,bytesMdl] = info.bytes; memReduction = 1 - [bytesMdl bytesCMdl]/infoMdlSV.bytes
memReduction = 1×2
0.0626 0.9996
В этом случае отбрасывание векторов поддержки снижает потребление памяти примерно на 6%. Сжатие и удаление векторов подложки уменьшает размер примерно на 99,96%.
Альтернативным способом управления векторами поддержки является уменьшение их количества во время обучения путем указания большего ограничения на коробку, например, 100. Несмотря на то, что модели SVM, в которых используется меньше векторов поддержки, более желательны и потребляют меньше памяти, увеличение значения ограничения поля приводит к увеличению времени обучения.
Удалить MdlSV и Mdl из рабочей области.
clear Mdl MdlSV
Оценка производительности образца Holdout
Вычислите классификационную ошибку выборки с удержанием. Постройте график выборок выборок.
oosLoss = loss(CMdl,X(oosIdx,:),Y(oosIdx))
oosLoss = 0
yHat = predict(CMdl,X(oosIdx,:)); nVec = 1:size(X,1); oosIdx = nVec(oosIdx); figure; for j = 1:9 subplot(3,3,j) imagesc(reshape(X(oosIdx(j),:),[d d])) h = gca; h.YDir = 'normal'; title(sprintf('Quadrant: %d',yHat(j))) end text(-1.33*d,4.5*d + 1,'Predictions','FontSize',17)

Модель не классифицирует по ошибке какие-либо наблюдения образцов в состоянии ожидания.
bayesopt | fitcsvm | kfoldLoss
[1] Хасти, Т., Р. Тибширани и Дж. Фридман. элементы статистического обучения, второе издание. Нью-Йорк: Спрингер, 2008.
[2] Кристианини, Н. и Дж. Шаве-Тейлор. Введение в поддержку векторных машин и других методов обучения на основе ядра. Кембридж, Великобритания: Cambridge University Press, 2000.
[3] Вентилятор, R.-E., P.-H. Чен и К.-Ж. Лин. «Выбор рабочего набора с использованием информации второго порядка для тренировочных машин поддержки векторов». Журнал исследований машинного обучения, том 6, 2005, стр. 1889-1918.
[4] Кекман В., Т. -М. Хуан и М. Фогт. «Итеративный алгоритм одиночных данных для обучения машин ядра из огромных наборов данных: теория и производительность». В поддержке векторных машин: теория и приложения. Под редакцией Липо Вана, 255-274. Берлин: Спрингер-Верлаг, 2005.