testcholdout

Сравнение предиктивной точности двух классификационных моделей

Синтаксис

h = testcholdout (YHat1,YHat2,Y)

h = testcholdout (YHat1,YHat2,Y,Name,Value)

[h, p, e1, e2] = testcholdout (___)

Описание

testcholdout статистически оценивает точность двух классификационных моделей. Функция сначала сравнивает их предсказанные метки с истинными метками, а затем обнаруживает, является ли разница между показателями неправильной классификации статистически значимой.

Можно оценить, отличается ли точность классификационных моделей или одна классификационная модель работает лучше другой. testcholdout может проводить несколько вариаций теста МакНемара, включая асимптотический тест, точно-условный тест и тест среднего p-значения. Для оценки с учетом затрат доступные тесты включают тест хи-квадрат (требуется лицензия Optimization Toolbox™) и тест отношения правдоподобия.

пример

h = testcholdout(YHat1,YHat2,Y) возвращает тестовое решение, проводя тест McNemar со средним значением p, из проверки нулевой гипотезы, что предсказанные метки класса YHat1 и YHat2 имеют одинаковую точность для прогнозирования меток истинного класса Y. Альтернативная гипотеза заключается в том, что метки имеют неравную точность.

h = 1 указывает на отклонение нулевой гипотезы на уровне значимости 5%. h = 0 указывает, что не отклонять нулевую гипотезу на уровне 5%.

пример

h = testcholdout(YHat1,YHat2,Y,Name,Value) возвращает результат проверки гипотезы с дополнительными опциями, указанными одним или несколькими Name,Value аргументы пары. Например, можно указать тип альтернативной гипотезы, указать тип теста или предоставить матрицу затрат.

пример

[h,p,e1,e2] = testcholdout(___) возвращает значение p для теста гипотезы (p) и соответствующие потери классификации каждого набора прогнозируемых меток класса (e1 и e2) с использованием любого из входных аргументов в предыдущих синтаксисах.

Примеры

свернуть все

Сравнение точности двух различных классификационных моделей

Открыть сценарий в реальном времени

Обучение двух классификационных моделей с использованием различных алгоритмов. Проведите статистический тест, сравнивая коэффициенты неправильной классификации двух моделей на удерживаемом наборе.

Загрузить ionosphere набор данных.

load ionosphere

Создайте раздел, равномерно разделяющий данные на наборы обучения и тестирования.

rng(1);                             % For reproducibility
CVP = cvpartition(Y,'holdout',0.5);
idxTrain = training(CVP);           % Training-set indices 
idxTest = test(CVP);                % Test-set indices

CVP является объектом раздела перекрестной проверки, определяющим обучающие и тестовые наборы.

Обучение модели SVM и ансамбля из 100 фасованных классификационных деревьев. Для модели SVM укажите использование ядра радиальной базовой функции и эвристической процедуры для определения масштаба ядра.

MdlSVM = fitcsvm(X(idxTrain,:),Y(idxTrain),'Standardize',true,...
    'KernelFunction','RBF','KernelScale','auto');
t = templateTree('Reproducible',true);  % For reproducibility of random predictor selections
MdlBag = fitcensemble(X(idxTrain,:),Y(idxTrain),'Method','Bag','Learners',t);

MdlSVM является обученным ClassificationSVM модель. MdlBag является обученным ClassificationBaggedEnsemble модель.

Маркировка наблюдений тестового набора с использованием обученных моделей.

YhatSVM = predict(MdlSVM,X(idxTest,:));
YhatBag = predict(MdlBag,X(idxTest,:));

YhatSVM и YhatBag являются векторами, продолжающими прогнозируемые метки классов соответствующих моделей.

Проверьте, имеют ли две модели одинаковую прогностическую точность.

h = testcholdout(YhatSVM,YhatBag,Y(idxTest))

h = logical
   0

h = 0 указывает на то, что не отвергать нулевую гипотезу о том, что две модели имеют одинаковую прогностическую точность.

Оцените, лучше ли классифицируется одна модель классификации, чем другая

Открыть сценарий в реальном времени

Обучите две модели классификации, используя один и тот же алгоритм, но настройте гиперпараметр, чтобы сделать алгоритм более сложным. Провести статистический тест для оценки того, имеет ли более простая модель лучшую точность в удерживаемых данных, чем более сложная модель.

Загрузить ionosphere набор данных.

load ionosphere;

Создайте раздел, равномерно разделяющий данные на наборы обучения и тестирования.

rng(1);                             % For reproducibility
CVP = cvpartition(Y,'holdout',0.5);
idxTrain = training(CVP);           % Training-set indices 
idxTest = test(CVP);                % Test-set indices

CVP является объектом раздела перекрестной проверки, определяющим обучающие и тестовые наборы.

Обучайте две модели SVM: одну, использующую линейное ядро (по умолчанию для двоичной классификации), и одну, использующую ядро радиальной базовой функции. Используйте масштаб ядра по умолчанию 1.

MdlLinear = fitcsvm(X(idxTrain,:),Y(idxTrain),'Standardize',true);
MdlRBF = fitcsvm(X(idxTrain,:),Y(idxTrain),'Standardize',true,...
    'KernelFunction','RBF');

MdlLinear и MdlRBF обучены ClassificationSVM модели.

Маркировка наблюдений тестового набора с использованием обученных моделей.

YhatLinear = predict(MdlLinear,X(idxTest,:));
YhatRBF = predict(MdlRBF,X(idxTest,:));

YhatLinear и YhatRBF являются векторами, продолжающими прогнозируемые метки классов соответствующих моделей.

Проверьте нулевую гипотезу о том, что более простая модель (MdlLinear) максимально точна, чем более сложная модель (MdlRBF). Так как размер тестового набора велик, проведите асимптотический тест McNemar и сравните результаты с тестом среднего значения (по умолчанию тест без учета затрат). Запрос на возврат значений p и коэффициентов неправильной классификации.

Asymp = zeros(4,1); % Preallocation
MidP = zeros(4,1); 

[Asymp(1),Asymp(2),Asymp(3),Asymp(4)] = testcholdout(YhatLinear,YhatRBF,Y(idxTest),...
    'Alternative','greater','Test','asymptotic');
[MidP(1),MidP(2),MidP(3),MidP(4)] = testcholdout(YhatLinear,YhatRBF,Y(idxTest),...
    'Alternative','greater');
table(Asymp,MidP,'RowNames',{'h' 'p' 'e1' 'e2'})

ans=4×2 table
            Asymp          MidP   
          __________    __________

    h              1             1
    p     7.2801e-09    2.7649e-10
    e1       0.13714       0.13714
    e2       0.33143       0.33143

Значение p близко к нулю для обоих тестов, что указывает на убедительные доказательства отклонения нулевой гипотезы о том, что более простая модель менее точна, чем более сложная модель. Независимо от того, какой тест вы указываете, testcholdout возвращает один и тот же тип меры неправильной классификации для обеих моделей.

Проведение сопоставления двух классификационных моделей с учетом затрат

Открыть сценарий в реальном времени

Для наборов данных с несбалансированными представлениями классов или если ложноположительные и ложноотрицательные затраты несбалансированы, можно статистически сравнить прогностическую производительность двух классификационных моделей, включив в анализ матрицу затрат.

Загрузить arrhythmia набор данных. Определите представления классов в данных.

load arrhythmia;
Y = categorical(Y);
tabulate(Y);

  Value    Count   Percent
      1      245     54.20%
      2       44      9.73%
      3       15      3.32%
      4       15      3.32%
      5       13      2.88%
      6       25      5.53%
      7        3      0.66%
      8        2      0.44%
      9        9      1.99%
     10       50     11.06%
     14        4      0.88%
     15        5      1.11%
     16       22      4.87%

Существует 16 классов, однако некоторые из них не представлены в наборе данных (например, класс 13). Большинство наблюдений классифицируются как не имеющие аритмии (класс 1). Набор данных является сильно дискретным с несбалансированными классами.

Объединить все наблюдения с аритмией (классы 2-15) в один класс. Удалите эти наблюдения с неизвестным статусом аритмии (класс 16) из набора данных.

idx = (Y ~= '16');
Y = Y(idx);
X = X(idx,:);
Y(Y ~= '1') = 'WithArrhythmia';
Y(Y == '1') = 'NoArrhythmia';
Y = removecats(Y);

Создайте раздел, равномерно разделяющий данные на обучающие и тестовые наборы.

rng(1);                             % For reproducibility
CVP = cvpartition(Y,'holdout',0.5);
idxTrain = training(CVP);           % Training-set indices 
idxTest = test(CVP);                % Test-set indices

CVP является объектом раздела перекрестной проверки, определяющим обучающие и тестовые наборы.

Создайте матрицу затрат таким образом, что неправильная классификация пациента с аритмией в класс «без аритмии» в пять раз хуже, чем неправильная классификация пациента без аритмии в класс аритмии. Правильная классификация не влечет за собой никаких затрат. Строки указывают истинный класс, а столбцы - прогнозируемый класс. При выполнении анализа с учетом затрат рекомендуется указать порядок классов.

Cost = [0 1;5 0];
ClassNames = {'NoArrhythmia','WithArrhythmia'};

Обучите два повышающих ансамбля из 50 деревьев классификации, один из которых использует AdaBoostM1, а другой - LogitBoost. Поскольку в наборе данных отсутствуют значения, укажите использование суррогатных разделений. Обучение моделей с использованием матрицы затрат.

t = templateTree('Surrogate','on');
numTrees = 50;
MdlAda = fitcensemble(X(idxTrain,:),Y(idxTrain),'Method','AdaBoostM1',...
    'NumLearningCycles',numTrees,'Learners',t,...
    'Cost',Cost,'ClassNames',ClassNames);
MdlLogit = fitcensemble(X(idxTrain,:),Y(idxTrain),'Method','LogitBoost',...
    'NumLearningCycles',numTrees,'Learners',t,...
    'Cost',Cost,'ClassNames',ClassNames);

MdlAda и MdlLogit обучены ClassificationEnsemble модели.

Маркировка наблюдений тестового набора с использованием обученных моделей.

YhatAda = predict(MdlAda,X(idxTest,:));
YhatLogit = predict(MdlLogit,X(idxTest,:));

YhatLinear и YhatRBF - векторы, содержащие прогнозируемые метки классов соответствующих моделей.

Проверить наличие AdaBoostM1 ансамбля (MdlAdaи ансамбль LogitBoost (MdlLogit) имеют равную точность прогнозирования. Предоставьте матрицу затрат. Проведите асимптотический тест, тест отношения правдоподобия и тест с учетом затрат (по умолчанию при прохождении матрицы затрат). Запрос на возврат p-значений и затрат на неправильную классификацию.

[h,p,e1,e2] = testcholdout(YhatAda,YhatLogit,Y(idxTest),'Cost',Cost)

h = logical
   0

p = 0.3334

e1 = 0.5581

e2 = 0.4698

Входные аргументы

свернуть все

`YHat1` - Прогнозируемые метки классов
категориальный массив | символьный массив | строковый массив | логический вектор | числовой вектор | клеточный массив символьных векторов

Прогнозируемые метки классов первой классификационной модели, указанные как категориальный, символьный или строковый массив, логический или числовой вектор или массив ячеек символьных векторов.

Если YHat1 является символьным массивом, то каждый элемент должен соответствовать одной строке массива.

YHat1, YHat2, и Y должны иметь одинаковую длину.

Это лучшая практика для YHat1, YHat2, и Y для совместного использования данных одного типа.

`YHat2` - Прогнозируемые метки классов
категориальный массив | символьный массив | строковый массив | логический вектор | числовой вектор | клеточный массив символьных векторов

Прогнозируемые метки классов второй классификационной модели, указанные как категориальный, символьный или строковый массив, логический или числовой вектор или массив ячеек символьных векторов.

Если YHat2 является символьным массивом, то каждый элемент должен соответствовать одной строке массива.

YHat1, YHat2, и Y должны иметь одинаковую длину.

Это лучшая практика для YHat1, YHat2, и Y для совместного использования одного и того же типа данных.

`Y` - Метки истинного класса
категориальный массив | символьный массив | строковый массив | логический вектор | числовой вектор | клеточный массив символьных векторов

Метки класса True, указанные как категориальный, символьный или строковый массив, логический или числовой вектор или массив ячеек символьных векторов.

Если Y является символьным массивом, то каждый элемент должен соответствовать одной строке массива.

YHat1, YHat2, и Y должны иметь одинаковую длину.

Это лучшая практика для YHat1, YHat2, и Y для совместного использования одного и того же типа данных.

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Пример: 'Alternative','greater','Test','asymptotic','Cost',[0 2;1 0] указывает, является ли первый набор первых предсказанных меток класса более точным, чем второй набор, проводит ли асимптотический тест McNemar и штрафует за неправильную классификацию наблюдений с истинной меткой ClassNames{1} вдвое больше, чем для неправильной классификации наблюдений с истинной меткой ClassNames{2}.

`'Alpha'` - Уровень значимости теста гипотез
`0.05` (по умолчанию) | скалярное значение в интервале (0,1)

Уровень значимости теста гипотез, указанный как пара, разделенная запятыми, состоящая из 'Alpha' и скалярное значение в интервале (0,1).

Пример: 'Alpha',0.1

Типы данных: single | double

`'Alternative'` - Альтернативная гипотеза для оценки
`'unequal'` (по умолчанию) | `'greater'` | `'less'`

Альтернативная гипотеза для оценки, указанная как пара, разделенная запятыми, состоящая из 'Alternative' и одно из значений, перечисленных в таблице.

Стоимость	Альтернативная гипотеза
`'unequal'` (по умолчанию)	Для прогнозирования `Y`, `YHat1` и `YHat2` имеют неравную точность.
`'greater'`	Для прогнозирования `Y`, `YHat1` является более точным, чем `YHat2`.
`'less'`	Для прогнозирования `Y`, `YHat1` является менее точным, чем `YHat2`.

Пример: 'Alternative','greater'

`'ClassNames'` - Названия классов
категориальный массив | символьный массив | строковый массив | логический вектор | числовой вектор | клеточный массив символьных векторов

Имена классов, указанные как разделенная запятыми пара, состоящая из 'ClassNames' и категориальный, символьный или строковый массив, логический или числовой вектор или массив ячеек символьных векторов. Необходимо установить ClassNames с использованием типа данных Y.

Если ClassNames является символьным массивом, то каждый элемент должен соответствовать одной строке массива.

Использовать ClassNames кому:

Укажите порядок любого измерения входного аргумента, соответствующего порядку класса. Например, использовать ClassNames для указания порядка размеров Cost.
Выберите подмножество классов для тестирования. Например, предположим, что набор всех различных имен классов в Y является {'a','b','c'}. Обучение и тестирование моделей с использованием наблюдений из классов 'a' и 'c' только, укажите 'ClassNames',{'a','c'}.

По умолчанию используется набор всех различающихся имен классов в Y.

Пример: 'ClassNames',{'b','g'}

`'Cost'` - Расходы на неправильную классификацию
квадратная матрица | массив структуры

Стоимость неправильной классификации, указанная как разделенная запятыми пара, состоящая из 'Cost' и квадратную матрицу или структурный массив.

При указании квадратной матрицы Cost, то Cost(i,j) - стоимость классификации точки по классу j если его истинный класс i. То есть строки соответствуют истинному классу, а столбцы - прогнозируемому классу. Определение порядка классов для соответствующих строк и столбцов Cost, дополнительно указать ClassNames аргумент пары имя-значение.
При указании структуры S, то S должны иметь два поля:
- S.ClassNames, который содержит имена классов в качестве переменной того же типа данных, что и Y. В этом поле можно указать порядок классов.
- S.ClassificationCosts, которая содержит матрицу затрат, со строками и столбцами, упорядоченными как в S.ClassNames.

При указании Cost, то testcholdout не может проводить односторонние, точные или промежуточные тесты. Необходимо также указать 'Alternative','unequal','Test','asymptotic'. Для получения информации о вариантах тестирования с учетом затрат см. CostTest аргумент пары имя-значение.

Передовой практикой является предоставление той же матрицы затрат, которая используется для обучения моделей классификации.

Значение по умолчанию: Cost(i,j) = 1 если i ~= j, и Cost(i,j) = 0 если i = j.

Пример: 'Cost',[0 1 2 ; 1 0 2; 2 2 0]

Типы данных: single | double | struct

`'CostTest'` - Тип теста с учетом затрат
`'likelihood'` (по умолчанию) | `'chisquare'`

Чувствительный к стоимости тип теста, указанный как разделенная запятыми пара, состоящая из 'CostTest' и 'chisquare' или 'likelihood'. Если матрица затрат не указана с помощью Cost аргумент пары имя-значение, testcholdout игнорирует CostTest.

В этой таблице представлены доступные варианты тестирования с учетом затрат.

Стоимость	Тип асимптотического теста	Требования
`'chisquare'`	Тест на хи-квадрат	Лицензия Optimization Toolbox для реализации `quadprog`(Панель инструментов оптимизации)
`'likelihood'`	Тест отношения правдоподобия	Ничего

Дополнительные сведения см. в разделе Тестирование с учетом затрат.

Пример: 'CostTest','chisquare'

`'Test'` - Тестирование для проведения
`'asymptotic'` | `'exact'` | `'midp'`

Испытание, указанное как пара, разделенная запятыми, состоящая из 'Test' и 'asymptotic', 'exact', и 'midp'. В этой таблице представлены доступные варианты тестирования без учета затрат.

Стоимость	Описание
`'asymptotic'`	Асимптотический тест МакНемара
`'exact'`	Точно условный тест Макнемара
`'midp'` (по умолчанию)	Тест McNemar среднего значения p

Дополнительные сведения см. в разделе Тесты McNemar.

Для тестирования с учетом затрат, Test должно быть 'asymptotic'. При указании Cost аргумент пары «имя-значение» и выберите тест, чувствительный к стоимости, с помощью CostTest аргумент пары имя-значение, 'asymptotic' является значением по умолчанию.

Пример: 'Test','asymptotic'

Примечание

NaNs, <undefined> значения, пустые векторы символов (''), пустые строки (""), и <missing> значения указывают отсутствующие значения данных. testcholdout:

Обрабатывает отсутствующие значения в YHat1 и YHat2 как неправильно классифицированные наблюдения.
Удаление отсутствующих значений в Y и соответствующие значения YHat1 и YHat2

Выходные аргументы

свернуть все

`h` - Результат проверки гипотезы
`1` | `0`

Результат проверки гипотезы, возвращенный как логическое значение.

h = 1 указывает на отклонение нулевой гипотезы в Alpha уровень значимости.

h = 0 указывает на отказ отклонить нулевую гипотезу в Alpha уровень значимости.

Типы данных: logical

`p` - p-значение
скаляр в интервале [0,1]

p-значение теста, возвращаемое в виде скаляра в интервале [0,1]. p - вероятность того, что статистика случайного теста является по меньшей мере такой же экстремальной, как статистика наблюдаемого теста, учитывая, что нулевая гипотеза верна.

testcholdout оценки p с использованием распределения статистики теста, которое варьируется в зависимости от типа теста. Дополнительные сведения о статистике тестов, полученной из доступных вариантов теста McNemar, см. в разделе Тесты McNemar. Дополнительные сведения о статистике тестов, полученной из тестов с учетом затрат, см. в разделе Тестирование с учетом затрат.

`e1` - классификационные потери;
скаляр

Потеря классификации, которая суммирует точность первого набора меток класса (YHat1) предсказание меток истинного класса (Y), возвращенный как скаляр.

Для тестирования без учета затрат, e1 - коэффициент неправильной классификации. То есть e1 - доля неправильно классифицированных наблюдений, которая является скаляром в интервале [0,1].

Для тестирования с учетом затрат, e1 - стоимость неправильной классификации. То есть e1 - средневзвешенное значение затрат на неправильную классификацию, в котором весами являются соответствующие оценочные пропорции неправильно классифицированных наблюдений.

`e2` - классификационные потери;
скаляр

Потеря классификации, которая суммирует точность второго набора меток класса (YHat2) предсказание меток истинного класса (Y), возвращенный как скаляр.

Для тестирования без учета затрат, e2 - коэффициент неправильной классификации. То есть e2 - доля неправильно классифицированных наблюдений, которая является скаляром в интервале [0,1].

Для тестирования с учетом затрат, e2 - стоимость неправильной классификации. То есть e2 - средневзвешенное значение затрат на неправильную классификацию, в котором весами являются соответствующие оценочные пропорции неправильно классифицированных наблюдений.

Подробнее

свернуть все

Тестирование с учетом затрат

Проводить тестирование с учетом затрат, когда несбалансирована стоимость неправильной классификации. Проводя чувствительный к затратам анализ, можно учесть несбалансированность затрат при обучении классификационных моделей и их статистическом сравнении.

Если стоимость неправильной классификации несбалансирована, то коэффициент неправильной классификации, как правило, является плохо выполняемой потерей классификации. Вместо этого используйте затраты на неправильную классификацию для сравнения классификационных моделей.

Затраты на неправильную классификацию часто несбалансированы в приложениях. Например, рассмотреть возможность классификации субъектов на основе набора предикторов на две категории: здоровые и больные. Неправильная классификация больного как здорового представляет опасность для жизни субъекта. Однако неправильная классификация здорового субъекта как больного обычно вызывает некоторые неудобства, но не представляет значительной опасности. В этой ситуации присваиваются такие затраты на неправильную классификацию, что неправильная классификация больного субъекта как здорового дороже, чем неправильная классификация здорового субъекта как больного.

Следующие определения суммируют тесты с учетом затрат. В определениях:

_nijk и ${\overset{}{λ}}_{^}$ ijk - количество и оценочная доля наблюдений тестового образца со следующими характеристиками. k - истинный класс, i - метка, назначенная первой классификационной моделью, и j - метка, назначенная второй классификационной моделью. Неизвестное истинное значение ${\overset{}{}}_{δ^}$ ijk _равно securityijk. Размер выборки тестового набора $\underset{равен}{}_{}_{}$ ∑i,j,knijk=ntest. $\underset{Кроме того,}{}_{} \underset{}{} {\overset{}{}}_{}$ ∑i,j,kπijk=∑i,j,kπ^ijk=1.
_cij - относительная стоимость присвоения метки j наблюдению с истинным классом i _cii = 0, _cij ≥ 0, и, по меньшей мере, для одной (i, j) пары, _cij > 0 .
Все подстрочные индексы принимают целочисленные значения от 1 до K, что является числом классов.
Ожидаемая разница в расходах на неправильную классификацию двух классификационных моделей составляет

$_{}^{}_{}^{}_{}^{δ=∑i=1K∑j=1K∑k=1K} (_{} cki_{-}_{ckj)}$ securityijk.
Критерий гипотезы:

$\begin{matrix} _{} \\ _{} H0:δ=0H1:δ≠0 \end{matrix} .$
Доступные чувствительные к стоимости тесты подходят для двухсторонних испытаний.

Доступные асимптотические тесты, которые учитывают несбалансированные затраты, являются тестом хи-квадрат и тестом отношения правдоподобия.

Тест хи-квадрат - статистика тестов хи-квадрат основана на статистике тестов Пирсона и Неймана хи-квадрат, но с поправочным коэффициентом Лапласа для учета любого _nijk = 0. Статистика теста:

$_{^{}}^{} \underset{}{} \underset{tχ2∗=∑i≠j∑k}{} \frac{{(_{} nijk + 1_{- (}^{} {\overset{}{ntest}}_{+}^{K3)} λ}^{}}{^_{} ijk} ($ 1)) 2nijk + 1.
Если $1 -_{^{}} {Fχ2}_{^{(}}^{} tχ2∗;1$ ) < α, то отклонить H0.
- ${\overset{}{δ}}_{^}^{ijk}$ (1) оцениваются путем $_{{минимизации}^{}}^{}$ tχ2∗ при условии, что δ = 0.
- $_{^{Fχ2}} (x;$ 1) - cdf, с одной степенью свободы, оцениваемой при x.
Тест отношения правдоподобия - тест отношения правдоподобия основан на _Nijk, которые представляют собой биномиальные случайные величины с размером выборки _ntest и вероятностью успеха _serverijk. Случайные величины представляют случайное число наблюдений с: истинным классом k, меткой i, присвоенной первой классификационной моделью, и меткой j, присвоенной второй классификационной моделью. Совместно распределение случайных величин является полиномиальным.
Статистика теста:

$_{}^{} \frac{tLRT∗=2log[P \underset{}{(}_{}_{}_{} {\overset{}{}}_{} {\overset{}{}}_{}^{\capi,j,kNijk=nijk;ntest,π^ijk=π^ijk (} 2}{)) \underset{P (}{}_{}_{}_{} {\overset{}{}}_{} {\overset{}{}}_{}^{} \capi,j,kNijk=nijk;ntest,π^ijk=π^ijk} ($ 3))].
Если $1 -_{^{}} {Fχ2}_{(}^{} tLRT∗;1)$ < α, то отклонить H0.
- ${\overset{}{δ}}_{^}^{ijk} (\frac{2_{) =}}{_{}}$ nijkntest - неограниченный MLE для securityijk.
- ${\overset{}{δ}}_{^}^{ijk} (\frac{3_{) =}}{_{}_{nijkntest} +_{λ} (}$ cki − ckj) - MLE при нулевой гипотезе, что δ = 0. λ - решение
  
  $\underset{}{} \frac{_{∑i,j,knijk} (_{} cki_{-}}{_{ckj)} {ntest}_{+} λ_{(}} cki$ − ckj) = 0.
- $_{^{Fχ2}} (x;$ 1) - cdf, с одной степенью свободы, оцениваемой при x.

Тесты McNemar

Тесты Макнемара - это тесты гипотез, которые сравнивают две пропорции популяции, решая при этом проблемы, возникающие в результате двух зависимых, согласованных пар выборок.

Одним из способов сравнения прогностической точности двух классификационных моделей является:

Разбейте данные на обучающие и тестовые наборы.
Обучение обеих моделей классификации с использованием обучающего набора.
Спрогнозировать метки классов с помощью тестового набора.
Сведите результаты в таблицу «два на два», аналогичную этой диаграмме.

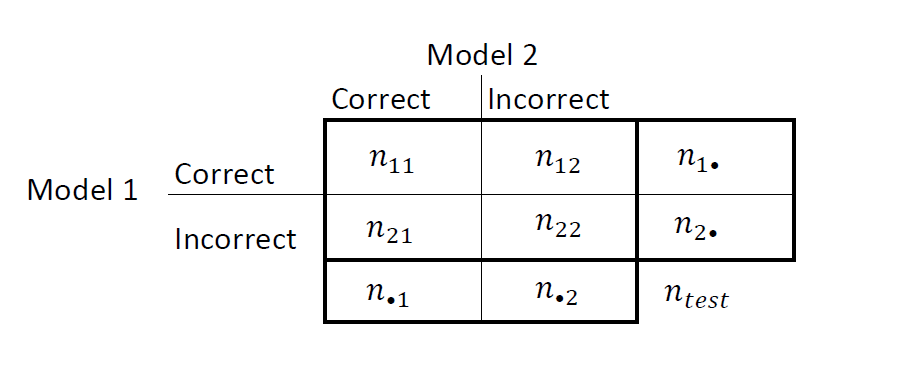
_nii - количество совпадающих пар, то есть количество наблюдений, которые обе модели классифицируют одинаково (правильно или неправильно). _nij, i ≠ j, - количество дискордантных пар, то есть количество наблюдений, которые модели классифицируют по-разному (правильно или неправильно).

Коэффициенты неправильной классификации для Моделей 1 и 2 составляют ${\overset{}{δ}}_{^} 2_{•} =$ n2 •/ ${\overset{}{n}}_{} и_{λ}^$ 2 = n • 2/n соответственно. Двусторонний тест для сравнения точности двух моделей

$\begin{matrix} _{}_{}_{} \\ _{}_{}_{H0:π•2=π2•H1:π•2≠π2} \end{matrix} •.$

Нулевая гипотеза предполагает, что популяция проявляет маргинальную однородность, что сводит нулевую гипотезу к $_{H0} :_{} security12_{=}$ security21. Также при нулевой гипотезе N12 ~ Биномиал (n12 ₊ n21,0,5) [1].

Эти факты являются основой для доступных вариантов теста Макнемара: асимптотических, точно-условных и среднезначных тестов Макнемара. Следующие определения суммируют доступные варианты.

Асимптотическая - асимптотическая статистика теста МакНемара и области отклонения (для уровня значимости α):
- Для односторонних тестов статистика теста равна
  
  $_{}^{ta1 } = \frac{_{}_{}}{\sqrt{_{}_{n12−n21n12+n21}}} .$
  Если $1 - Start(_{}^{} |t1∗|)$ < α, где Startявляется стандартным гауссовым cdf, то отклоните H0.
- Для двусторонних тестов статистика теста равна
  
  $_{}^{ta2 } = \frac{{_{}_{} (n12-n21)}^{}}{_{}_{2n12+n21}} .$
  Если $1 -_{^{}} {Fχ2}_{}^{(} t2∗;m$ ) < α, $_{^{}} где Fχ2$ (x; m) _- cdf, вычисленный при x, то отклонить H0.
Асимптотический тест требует теории больших выборок, в частности, гауссова аппроксимации к биномиальному распределению.
- Общее число несогласованных пар, $_{nd} =_{} {n12}_{+}$ n21, должно быть больше 10 ([1], Ch. 10,1,4).
- В целом асимптотические тесты не гарантируют номинального покрытия. Наблюдаемая вероятность ложного отклонения нулевой гипотезы может превышать α, как предложено в имитационных исследованиях в [18]. Однако асимптотический тест Макнемара хорошо работает с точки зрения статистической мощности.
Точная - условная - точная условная статистика теста Макнемара и области отклонения (для уровня значимости α) являются ([36], [38]):
- Для односторонних тестов статистика теста равна
  
  $_{}^{t1 } =_{n12} .$
  Если $_{FBin} (_{}^{}_{} t1*;nd,0.5)$ < α, $_{где} FBin (x;$ n, p) является биномиальным cdf с размером выборки n и вероятностью успеха p, оцененной при x, то отклонить H0.
- Для двусторонних тестов статистика теста равна
  
  $_{}^{} t2∗=min (_{} n12,_{} n21$ ).
  Если $_{FBin} (_{}^{}_{} t2*;nd,0.5) <$ α/2, то отклоните H0.
Точный условный тест всегда достигает номинального покрытия. Исследования моделирования в [18] показывают, что тест является консервативным, а затем показывают, что тест не обладает статистической мощностью по сравнению с другими вариантами. Для небольших или очень дискретных испытательных образцов рекомендуется использовать испытание среднего значения p ([1], гл. 3.6.3).
Тест среднего p-значения - статистика теста среднего p-значения McNemar и области отклонения (для уровня значимости α) являются ([32]):
- Для односторонних тестов статистика теста равна
  
  $_{}^{t1 } =_{n12} .$
  Если $_{FBin} (_{}^{}_{}_{} t1*-1;n12+n21,0.5) +_{}_{0.5fBin}^{} (_{}_{}$ t1∗;n12+n21,0.5) < α, $_{} где FBin$ (x; n $,_{p)} и$ fBin (x; n, p) являются биномиальными cdf и pdf соответственно с размером выборки n и вероятностью успеха p, оцененной при x, то отклонить H0.
- Для двусторонних тестов статистика теста равна
  
  $_{}^{} t2∗=min (_{} n12,_{} n21$ ).
  Если $_{FBin} (_{}^{}_{}_{} t2*-1;n12+n21-1,0.5) +_{}_{0.5fBin}^{} (_{}_{} t2*;n12+n21,0.5)$ < α/2, то отбраковать H0.
Тест среднего p-значения обращается к чрезмерно консервативному поведению теста точного условия. Исследования моделирования в [18] показывают, что этот тест достигает номинального охвата и обладает хорошей статистической мощностью.

Классификационные потери

Потери классификации указывают на точность классификационной модели или набора прогнозируемых меток. Двумя классификационными потерями являются коэффициент неправильной классификации и стоимость.

testcholdout возвращает потери классификации (см. e1 и e2) при альтернативной гипотезе (то есть неограниченных классификационных потерях). _nijk - количество наблюдений тестовой выборки с: истинным классом k, меткой i, присвоенной первой классификационной моделью, и меткой j, присвоенной второй классификационной моделью. Соответствующая оценочная пропорция δ ${\overset{}{}}_{^} \frac{{ijk}_{=}}{_{}}$ nijkntest. Размер выборки тестового набора $\underset{равен}{}_{}_{}$ ∑i,j,knijk=ntest. Индексы берутся от 1 до K, количество классов.

Частота неправильной классификации, или ошибка классификации, является скаляром в интервале [0,1], представляющем долю неправильной классификации наблюдений. То есть коэффициент неправильной классификации для первой классификационной модели равен

$_{}_{}^{}_{}^{}_{}^{} {\overset{}{}}_{e1=∑j=1K∑k=1K∑i≠kπ^ijk} .$
Для коэффициента неправильной классификации второй классификационной модели (e2) переключите индексы i и j в формуле.
Точность классификации уменьшается по мере увеличения коэффициента неправильной классификации до 1.
Стоимость неправильной классификации является неотрицательным скаляром, который является мерой качества классификации относительно значений указанной матрицы затрат. Его толкование зависит от указанных затрат на неправильную классификацию. Затраты на неправильную классификацию - это средневзвешенное значение затрат на неправильную классификацию (указанное в матрице затрат, C), в которой весовые коэффициенты являются соответствующими оценочными пропорциями неправильно классифицированных наблюдений. Стоимость неправильной классификации для первой модели классификации составляет

$_{}_{}^{}_{}^{}_{}^{} {\overset{}{}}_{}_{e1=∑j=1K∑k=1K∑i≠kπ^ijkcki},$
где _ckj - стоимость классификации наблюдения по классу j, если его истинным классом является k. Для стоимости неправильной классификации второй классификационной модели (e2) переключите индексы i и j в формуле.
Как правило, для матрицы фиксированных затрат точность классификации снижается по мере увеличения затрат на неправильную классификацию.

Совет

Это хорошая практика для получения прогнозируемых меток классов путем передачи любой обученной модели классификации и новых данных предиктора в predict способ. Например, для получения информации о прогнозируемых метках из модели SVM см. predict.
Чувствительные к затратам тесты выполняют численную оптимизацию, что требует дополнительных вычислительных ресурсов. Тест отношения правдоподобия проводит численную оптимизацию косвенно путем нахождения корня множителя Лагранжа в интервале. Для некоторых наборов данных, если корень лежит близко к границам интервала, то метод может завершиться ошибкой. Поэтому, если у вас есть лицензия Optimization Toolbox, рассмотрите возможность проведения теста хи-квадрат с учетом затрат. Дополнительные сведения см. в разделе CostTest и тестирование с учетом затрат.

Ссылки

[1] Agresti, A. Категориальный анализ данных, 2-й ред. Джон Уайли и сыновья, Inc.: Хобокен, Нью-Джерси, 2002.

[2] Фагерлан, М.В., С. Лидерсен и П. Лааке. «Тест McNemar для двоичных согласованных пар данных: Mid-p и асимптотические лучше, чем точные условные». Методология медицинских исследований BMC. Том 13, 2013, стр. 1-8.

[3] Ланкастер, H.O. «Тесты значимости в дискретных распределениях». JASA, том 56, номер 294, 1961, стр. 223-234.

[4] McNemar, Q. «Примечание об ошибке выборки разницы между коррелированными пропорциями или процентами». Психометрика, т. 12, № 2, 1947, с. 153-157.

[5] Мостеллер, Ф. «Некоторые статистические проблемы в измерении субъективной реакции на наркотики». Биометрия, т. 8, № 3, 1952, с. 220-226.

См. также

testckfold

Темы

Тесты гипотез

Представлен в R2015a

Документация

testcholdout

Синтаксис

Описание

Примеры

Сравнение точности двух различных классификационных моделей

Оцените, лучше ли классифицируется одна модель классификации, чем другая

Проведение сопоставления двух классификационных моделей с учетом затрат

Входные аргументы

`Y` - Метки истинного класса
категориальный массив | символьный массив | строковый массив | логический вектор | числовой вектор | клеточный массив символьных векторов

Аргументы пары «имя-значение»

`'Alpha'` - Уровень значимости теста гипотез
`0.05` (по умолчанию) | скалярное значение в интервале (0,1)

`'Alternative'` - Альтернативная гипотеза для оценки
`'unequal'` (по умолчанию) | `'greater'` | `'less'`

`'ClassNames'` - Названия классов
категориальный массив | символьный массив | строковый массив | логический вектор | числовой вектор | клеточный массив символьных векторов

`'Cost'` - Расходы на неправильную классификацию
квадратная матрица | массив структуры

`'CostTest'` - Тип теста с учетом затрат
`'likelihood'` (по умолчанию) | `'chisquare'`

`'Test'` - Тестирование для проведения
`'asymptotic'` | `'exact'` | `'midp'`

Выходные аргументы

`h` - Результат проверки гипотезы
`1` | `0`

`p` - p-значение
скаляр в интервале [0,1]

`e1` - классификационные потери;
скаляр

`e2` - классификационные потери;
скаляр

Подробнее

Тестирование с учетом затрат

Тесты McNemar

Классификационные потери

Совет

Ссылки

См. также

Темы

Документация по инструментам для статистического и машинного обучения

Поддержка

Документация

testcholdout

Синтаксис

Описание

Примеры

Сравнение точности двух различных классификационных моделей

Оцените, лучше ли классифицируется одна модель классификации, чем другая

Проведение сопоставления двух классификационных моделей с учетом затрат

Входные аргументы

Y - Метки истинного класса категориальный массив | символьный массив | строковый массив | логический вектор | числовой вектор | клеточный массив символьных векторов

Аргументы пары «имя-значение»

'Alpha' - Уровень значимости теста гипотез 0.05 (по умолчанию) | скалярное значение в интервале (0,1)

'Alternative' - Альтернативная гипотеза для оценки 'unequal' (по умолчанию) | 'greater' | 'less'

'ClassNames' - Названия классов категориальный массив | символьный массив | строковый массив | логический вектор | числовой вектор | клеточный массив символьных векторов

'Cost' - Расходы на неправильную классификацию квадратная матрица | массив структуры

'CostTest' - Тип теста с учетом затрат 'likelihood' (по умолчанию) | 'chisquare'

'Test' - Тестирование для проведения 'asymptotic' | 'exact' | 'midp'

Выходные аргументы

h - Результат проверки гипотезы 1 | 0

p - p-значение скаляр в интервале [0,1]

e1 - классификационные потери; скаляр

e2 - классификационные потери; скаляр

Подробнее

Тестирование с учетом затрат

Тесты McNemar

Классификационные потери

Совет

Ссылки

См. также

Темы

Документация по инструментам для статистического и машинного обучения

Поддержка

`'Alpha'` - Уровень значимости теста гипотез
`0.05` (по умолчанию) | скалярное значение в интервале (0,1)

`'Alternative'` - Альтернативная гипотеза для оценки
`'unequal'` (по умолчанию) | `'greater'` | `'less'`

`'Cost'` - Расходы на неправильную классификацию
квадратная матрица | массив структуры

`'CostTest'` - Тип теста с учетом затрат
`'likelihood'` (по умолчанию) | `'chisquare'`

`'Test'` - Тестирование для проведения
`'asymptotic'` | `'exact'` | `'midp'`

`h` - Результат проверки гипотезы
`1` | `0`

`p` - p-значение
скаляр в интервале [0,1]

`e1` - классификационные потери;
скаляр

`e2` - классификационные потери;
скаляр