Документация

CWT как метод фильтрации

Непрерывное вейвлет-преобразование (CWT) вычисляет внутреннее произведение сигнала, $$f(t$$), с транслированными и расширенными версиями анализирующего вейвлета, $$start(t$$). Определение CWT:

Можно также интерпретировать CWT как частотную фильтрацию сигнала, переписав CWT как обратное преобразование Фурье.

где $$\stackrel{}{f}^($$λ) $$\stackrel{}{и}start^$$(λ) - преобразования Фурье сигнала и вейвлета.

Из предыдущих уравнений видно, что растягивание вейвлета во времени приводит к тому, что его поддержка в частотной области уменьшается. В дополнение к уменьшению поддержки частоты центральная частота импульса смещается в сторону более низких частот. Следующий рисунок демонстрирует этот эффект для гипотетического вейвлет и масштабных (расширительных) факторов 1,2 и 4.

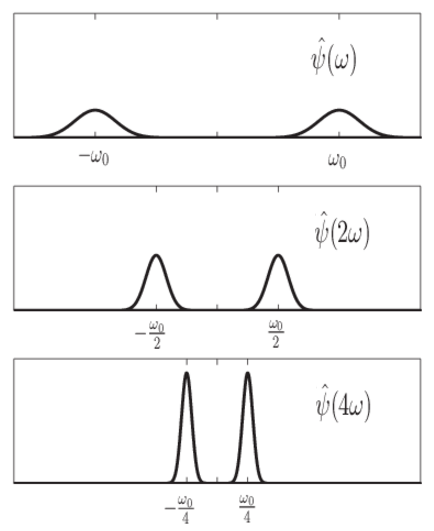
Это изображает CWT как полосовую фильтрацию входного сигнала. Коэффициенты CWT на более низких шкалах представляют энергию во входном сигнале на более высоких частотах, а коэффициенты CWT на более высоких шкалах представляют энергию во входном сигнале на более низких частотах. Однако, в отличие от полосовой фильтрации Фурье, ширина полосового фильтра в CWT обратно пропорциональна масштабу. Ширина фильтров CWT уменьшается с увеличением масштаба. Это следует из зависимостей неопределённости между временем и частотной поддержкой сигнала: чем шире поддержка сигнала во времени, тем уже его поддержка в частоте. Обратное отношение также сохраняется.

При вейвлет-преобразовании определяется масштаб или операция расширения для сохранения энергии. Для сохранения энергии при уменьшении частотной поддержки требуется, чтобы пиковый уровень энергии увеличивался. Осуществление cwt в вейвлет Toolbox™ использует нормализацию L1. Коэффициент качества или коэффициент Q фильтра - это отношение его пиковой энергии к полосе пропускания. Поскольку уменьшение или растягивание частотной поддержки импульса приводит к соразмерному увеличению или уменьшению его пиковой энергии, импульсы часто называют фильтрами постоянного Q.

Непрерывное вейвлет-преобразование на основе DFT

Уравнение в предыдущем разделе определяло CWT как обратное преобразование Фурье произведения преобразований Фурье.

Переменная времени в обратном преобразовании Фурье является параметром преобразования, b.

Это говорит о том, что CWT можно вычислить с помощью обратного преобразования Фурье. Поскольку существуют эффективные алгоритмы для вычисления дискретного преобразования Фурье и его обратного преобразования, часто можно добиться значительной экономии, используя fft и ifft по возможности.

Чтобы получить изображение CWT в области Фурье, начните с определения вейвлет-преобразования:

При определении:

можно переписать вейвлет-преобразование как

который явно выражает CWT как свертку.

Для реализации дискретизированной версии CWT предположим, что входная последовательность является вектором длины N, x [n]. Дискретная версия предыдущего свёртки:

Для получения CWT необходимо вычислить свертку для каждого значения параметра сдвига b и повторить этот процесс для каждого масштаба a.

Однако, если две последовательности являются циклически растянутыми (периодизированными до длины N), можно выразить круговую свертку как произведение дискретных преобразований Фурье. CWT - это обратное преобразование Фурье произведения.

где Δt - интервал выборки (период).

Выражение CWT как обратного преобразования Фурье позволяет использовать вычислительно-эффективное fft и ifft алгоритмы снижения стоимости вычислительных сверток.

cwt функция реализует CWT.