Непрерывное 1-D вейвлет-преобразование
Посмотрите cwt для получения информации о старой версии cwt. Более старая версия больше не рекомендуется.
wt = cwt(x)x. Вход, x, является вектором с реальными или комплексными значениями или одной переменной, регулярно дискретизируемым расписанием, и должен иметь по крайней мере четыре выборки. CWT получают, используя аналитический вейвлет Морса с параметром симметрии (гамма), равным 3, и произведением временной полосы, равным 60. cwt использует 10 голосов на октаву. Минимальная и максимальная шкалы определяются автоматически на основе разброса энергии вейвлета по частоте и времени. Если x вещественно-значимый, wt - матрица 2-D, где каждая строка соответствует одной шкале. Размер столбца wt равна длине x. Если x является комплекснозначным, wt является 3-D матрицей, где первая страница является CWT для положительных шкал (аналитическая часть или компонент против часовой стрелки), а вторая страница является CWT для отрицательных шкал (антианалитическая часть или компонент по часовой стрелке).
cwt функция использует нормализацию L1. При L1 нормализации, если вы имеете равные амплитудные колебательные компоненты в данных в различных масштабах, они будут иметь одинаковую величину в CWT. Использование L1 нормализации показывает более точное представление сигнала. См. раздел L1 Норма для CWT и непрерывного вейвлет-преобразования двух сложных экспоненциалов.
[ определяет частоту выборки, wt,f] = cwt(___,fs)fs, в Гц как положительный скаляр. cwt использование fs чтобы определить преобразования масштаба в частоту и вернуть частоты f в Гц. Если частота выборки не указана, cwt прибыль f в циклах на образец. Если вход x является сложным, преобразования масштаба в частоту применяются к обеим страницам wt. Если x является расписанием, вы не можете указать fs. fs определяется из RowTimes расписания.
[ определяет период выборки, wt,period] = cwt(___,ts)ts, как положительный duration скаляр. duration может быть в годах, днях, часах, минутах или секундах. cwt использование ts для вычисления преобразования масштаба в период и возврата периодов времени в period. Массив длительностей в period имеет то же свойство формата, что и ts. Если вход x является сложным, преобразования масштаба в период применяются к обеим страницам wt. Если x является расписанием, вы не можете указать ts. ts определяется из RowTimes расписания при установке 'PeriodLimits' пара имя-значение.
[___] = cwt(___, возвращает CWT с дополнительными опциями, указанными одним или несколькими Name,Value)Name,Value аргументы пары.
[___, возвращает банк фильтров, используемый в CWT. Посмотрите coi,fb] = cwt(___)cwtfilterbank.
[___, возвращает коэффициенты масштабирования, если анализирующий вейвлет fb,scalingcfs] = cwt(___)'morse' или 'amor'. Коэффициенты масштабирования не поддерживаются для ударного импульса.
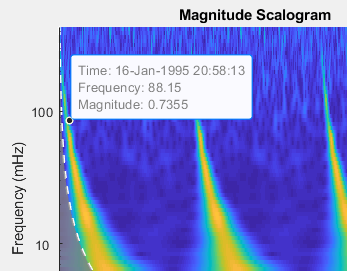
cwt(___) без выходных аргументов отображает скалограмму CWT. Скалограмма - это абсолютное значение CWT, отображаемое как функция времени и частоты. Строят график частоты в логарифмическом масштабе. На графике также показан конус влияния, показывающий, где краевые эффекты становятся значительными. Серые области за пределами пунктирной белой линии отделяют области, где краевые эффекты значительны. Если входной сигнал является комплекснозначным, то положительная (против часовой стрелки) и отрицательная (по часовой стрелке) составляющие строятся в отдельных скалограммах.
Если частота выборки или период выборки не указаны, то эти частоты отображаются в циклах на выборку. Если указана частота дискретизации, частоты будут в Гц. Если указан период выборки, скалограмма отображается как функция времени и периодов. Если входной сигнал является графиком, скалограмма строится как функция времени и частоты в герцах и использует RowTimes в качестве основы для оси времени.
Чтобы увидеть время, частоту и величину точки скалограммы, включите подсказки данных на панели инструментов осей рисунков и щелкните нужную точку в скалограмме.
Примечание
Перед построением графика, cwt очищает (clf) текущий показатель. Для построения графика скалограммы на вложенном графике используется функция печати. См. раздел Печать скалограммы CWT в подграфе.
При выполнении нескольких CWT, например, в цикле for, рекомендуется сначала создать cwtfilterbank и затем используйте wt объектная функция. Этот рабочий процесс сводит к минимуму накладные расходы и повышает производительность. См. Использование банка фильтров CWT для нескольких временных рядов.
[1] Лилли, Дж. М. и С. С. Ольхеде. «Обобщенные вейвлеты Морса как суперсемейство аналитических вейвлетов». Транзакции IEEE по обработке сигналов 60, № 11 (ноябрь 2012 г.): 6036-6041. https://doi.org/10.1109/TSP.2012.2210890.
[2] Лилли, Дж. М. и С.К. Ольхеде. «Свойства более высокого порядка аналитических вейвлетов». Транзакции IEEE по обработке сигналов 57, № 1 (январь 2009 года): 146-160. https://doi.org/10.1109/TSP.2008.2007607.
[3] Лилли, J. M. jLab: Пакет анализа данных для Matlab, версия 1.6.2. 2016. http://www.jmlilly.net/jmlsoft.html.
[4] Лилли, Джонатан М. «Анализ элементов: метод на основе вейвлета для анализа локализованных во времени событий в шумных временных рядах». Труды Королевского общества A: Математические, физические и инженерные науки 473, № 2200 (30 апреля 2017): 20160776. https://doi.org/10.1098/rspa.2016.0776.
cwtfilterbank | cwtfreqbounds | icwt