Вейвлет - это форма волны с фактически ограниченной длительностью, которая имеет среднее значение, равное нулю и ненулевой норме.
Многие сигналы и изображения, представляющие интерес, демонстрируют кусочно гладкое поведение, пунктуированное переходными процессами. Речевые сигналы характеризуются короткими пакетами, кодирующими согласные, за которыми следуют установившиеся колебания, указывающие на гласные. Естественные изображения имеют края. Финансовые временные ряды демонстрируют переходное поведение, которое характеризует быстрые подъемы и спады в экономических условиях. В отличие от базиса Фурье, вейвлет-базы развиты в малом представлении кусочно-регулярных сигналов и изображений, которые включают переходное поведение.
Сравните вейвлеты с синусоидальными волнами, которые являются основой анализа Фурье. Синусоиды не имеют ограниченной продолжительности - они простираются от минус до плюс бесконечности. В то время как синусоиды являются гладкими и предсказуемыми, вейвлеты имеют тенденцию быть нерегулярными и асимметричными.
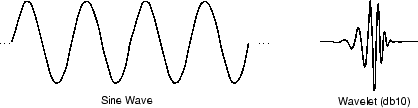
Анализ Фурье состоит из разделения сигнала на синусоидальные волны различных частот. Аналогично, вейвлет-анализ представляет собой разделение сигнала на сдвинутые и масштабированные версии исходного (или материнского) вейвлета.
Просто глядя на снимки вейвлетов и синусоидальных волн, вы можете интуитивно видеть, что сигналы с резкими изменениями могут быть лучше проанализированы с нерегулярным вейвлетом, чем с гладкой синусоидой.
Также имеет смысл, что локальные признаки могут быть описаны лучше с вейвлетами, которые имеют локальную протяженность. Следующий пример иллюстрирует это для простого сигнала, состоящего из синусоидальной волны с разрывом.
Этот пример показывает, что вейвлет-анализ может локализовать разрыв в синусоиде.
Создайте 1-Hz синусоидальную волну, дискретизированную на частоте 100 Гц. Длительность синусоидальной волны составляет одну секунду. Синусоидальная волна имеет разрыв при 0,5 с.
t = linspace(0,1,100)'; x = sin(2*pi*t); x1 = x-0.15; y = zeros(size(x)); y(1:length(y)/2) = x(1:length(y)/2); y(length(y)/2+1:end) = x1(length(y)/2+1:end); stem(t,y,'markerfacecolor',[0 0 1]); xlabel('Seconds'); ylabel('Amplitude');

Получение недекимированного дискретного вейвлет-преобразования синусоидальной волны с использованием 'sym2' вейвлет и постройте график коэффициентов вейвлета (детализации) вместе с исходным сигналом.
[swa,swd] = swt(y,1,'sym2'); subplot(211) stem(t,y,'markerfacecolor',[0 0 1]); title('Original Signal'); subplot(212) stem(t,swd,'markerfacecolor',[0 0 1]); title('Level 1 Wavelet Coefficients');

Сравните содействующие величины Фурье для волны синуса на 1 Гц с и без неоднородности.
dftsig = fft([x y]); dftsig = dftsig(1:length(y)/2+1,:); df = 100/length(y); freq = 0:df:50; stem(freq,abs(dftsig)); xlabel('Hz'); ylabel('Magnitude'); legend('sine wave','sine wave with discontinuity');

Существует минимальная разница в значениях коэффициентов Фурье. Поскольку дискретные базисные векторы Фурье имеют поддержку в течение всего временного интервала, дискретное преобразование Фурье не обнаруживает разрыв так же эффективно, как вейвлет-преобразование.
Сравните вейвлет-коэффициенты уровня 1 для синусоидальной волны с разрывом и без него.
[swax,swdx] = swt(x,1,'sym2'); subplot(211) stem(t,swd); title('Sine Wave with Discontinuity (Wavelet Coefficients)'); subplot(212) stem(t,swdx); title('Sine Wave (Wavelet Coefficients)');

Вейвлет-коэффициенты двух сигналов демонстрируют значительную разницу. Вейвлет-анализ часто способен выявить характеристики сигнала или изображения, которые другие методы анализа пропускают, такие как тренды, точки распада, разрывы в высших производных и самоподобие. Кроме того, поскольку вейвлеты обеспечивают другой вид данных, чем те, которые представлены методами Фурье, вейвлет-анализ часто может значительно сжимать или подавлять сигнал без заметного ухудшения.