Мультисигнальное 1-D вейвлет-пакетное преобразование
wpt = dwpt(X)X. Вход X - действительный вектор, матрица или расписание. По умолчанию fk18 используется вейвлет, а уровень разложения равен floor(log2(Ns)), где Ns - количество выборок данных. Вейвлет-преобразование пакетов wpt - массив ячеек 1-by-N, где N = 2^floor(log2(Ns)).
[ также возвращает уровни преобразования узлов wpt,l,packetlevels] = dwpt(___)wpt с использованием любого из предыдущих синтаксисов.
[ также возвращает центральные частоты приближенных полос пропускания в циклах на выборку с использованием любого из предыдущих синтаксисов.wpt,l,packetlevels,f] = dwpt(___)
[ также возвращает относительную энергию для вейвлет-пакетов в wpt,l,packetlevels,f,re] = dwpt(___)wpt с использованием любого из предыдущих синтаксисов. Относительная энергия представляет собой долю энергии, содержащейся в каждом вейвлет-пакете по уровню.
[___] = dwpt(___, указывает параметры, использующие аргументы пары имя-значение в дополнение к входным аргументам в предыдущих синтаксисах. Например, Name,Value)'Level',4 определяет уровень разложения.
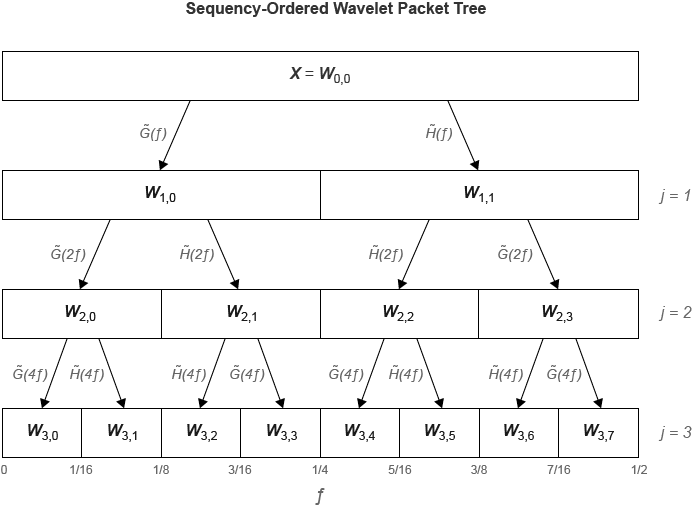
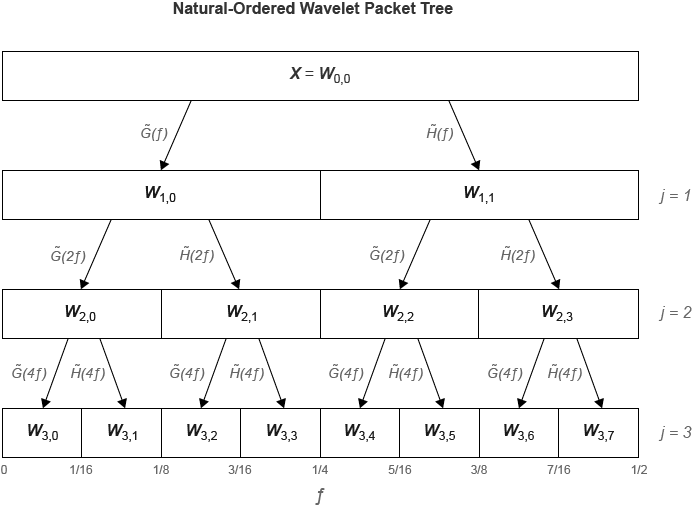
dwpt функция выполняет дискретное вейвлет-пакетное преобразование и формирует упорядоченное по последовательности вейвлет-пакетное дерево. Сравните упорядоченные по последовательности и нормальные деревья (Paley). f) является фильтром анализа масштабирования (нижних частот), (f) представляет фильтр анализа вейвлет (верхних частот). На метках внизу показано разделение частотной оси [0, ½].
[1] Викерхаузер, Младен Виктор. Адаптированный вейвлет-анализ от теории к программному обеспечению. Уэлсли, Массачусетс: А.К. Питерс, 1994.
[2] Персиваль, D. B. и А. Т. Уолден. Вейвлет-методы для анализа временных рядов. Кембридж, Великобритания: Cambridge University Press, 2000.
[3] Столовая гора, Гектор. «Адаптированные вейвлеты для обнаружения шаблона». В процессе распознавания образов, анализа изображений и приложений, под редакцией Альберто Санфелиу и Мануэля Лазо Кортеса, 3773: 933-44. Берлин, Гейдельберг: Springer Berlin Heidelberg, 2005. https://doi.org/10.1007/11578079_96 .