В этом примере показано, как использовать инструмент Continuous Wavelet 1-D для анализа шумного синусоидального сигнала.
Запустите инструмент Continuous Wavelet 1-D Tool. В подсказке MATLAB ® введите
waveletAnalyzer
Появится вейвлет-анализатор.
Выберите пункт меню Continuous Wavelet 1-D.
Появляется инструмент непрерывного вейвлет-анализа для 1-D данных сигнала.
Загрузите сигнал.
В командной строке MATLAB введите
load noissin;
noissin переменная. Нажмите кнопку OK для импорта шумового синусоидального сигнала.Значение по умолчанию для периода выборки равно 1 (секунде).
Выполнение непрерывного вейвлет-преобразования.
Чтобы начать наш анализ, давайте выполним анализ с помощью db4 вейвлет в масштабах от 1 до 48, так же, как мы использовали функции командной строки в предыдущем разделе.
В правой верхней части инструмента Continuous Wavelet 1-D выберите db4 вейвлет и шкала 1-48.
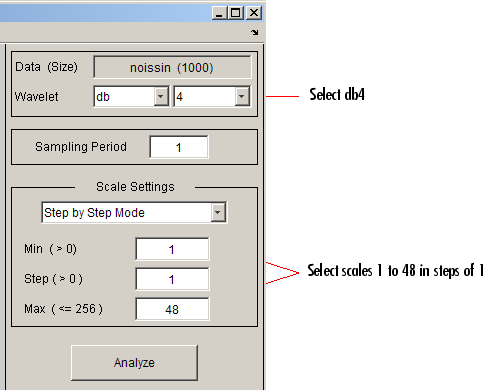
Нажмите кнопку «Анализ».
После паузы для вычисления инструмент отображает график коэффициентов, линейный график коэффициентов, соответствующий шкале a = 24, и локальный график максимумов, который отображает цепочку по масштабам (от a = 48 до a = 1) локальных максимумов коэффициентов.
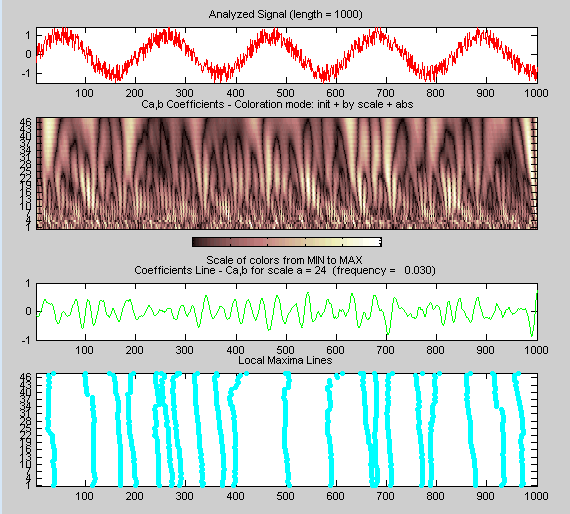
Просмотр строки вейвлет-коэффициентов.
Выберите другую шкалу a = 40, щелкнув правой кнопкой мыши на графике коэффициентов. Для получения более точной информации о выборе требуемого масштаба см. шаг 9.
Нажмите кнопку «Создать строку коэффициентов». Инструмент обновляет график.

Просмотр строки максимума.
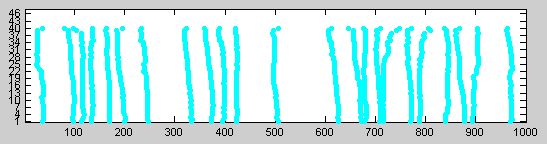
Нажмите кнопку Обновить строку максимума (Refresh Maxima Line). График локальных максимумов отображает цепочку по масштабам коэффициентов локальных максимумов от a = 40 до a = 1.
Удерживайте правую кнопку мыши над графиком коэффициентов. Положение мыши задается рамкой Info (расположена в нижней части экрана) по расположению (X) и шкале (Sca).
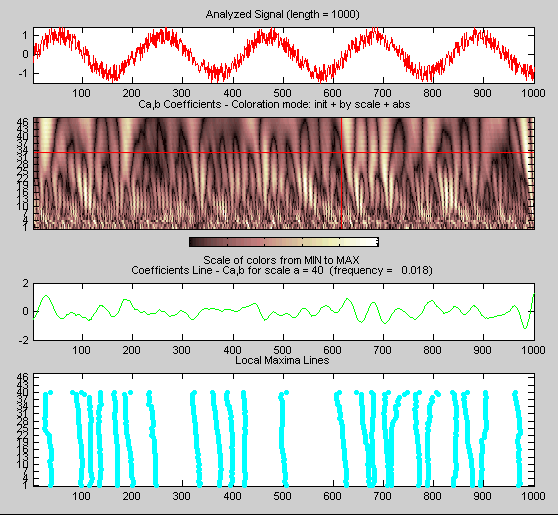
Переключение с масштаба на псевдочастотную информацию.
С помощью кнопки опции в правой части экрана выберите «Частоты» вместо «Масштаб». Снова удерживайте правую кнопку мыши над графиком коэффициентов, положение мыши задается с точки зрения местоположения (X) и частоты (Frq) в Герце.
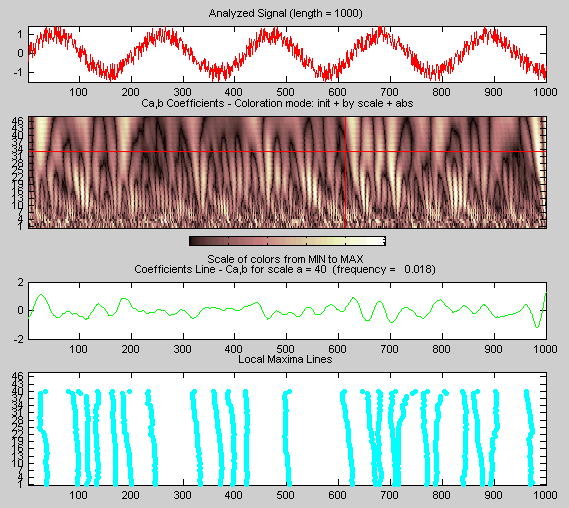
Это средство позволяет интерпретировать масштаб в терминах связанной псевдочастотности, которая зависит от вейвлета и периода дискретизации..
Отмените выбор последних двух графиков с помощью флажков в рамке Выбранные оси (Selected Axes).
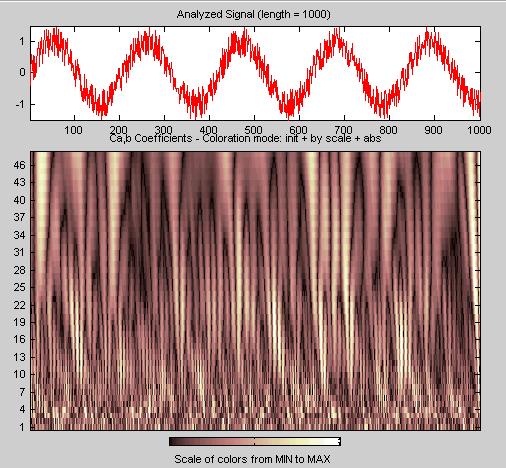
Увеличьте изображение деталей.
Перетащите коробку с резиновой лентой (удерживая левую кнопку мыши) над частью сигнала, который требуется увеличить.
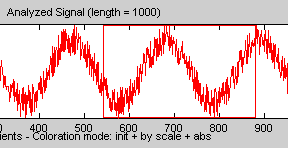
Нажмите кнопку X + (расположенную в нижней части экрана), чтобы увеличить изображение только по горизонтали.
![]()
Инструмент Continuous Wavelet 1-D увеличивает отображаемый график сигналов и коэффициентов (дополнительные сведения о масштабировании см. в разделе Соединение графиков в руководстве пользователя Wavelet Toolbox).
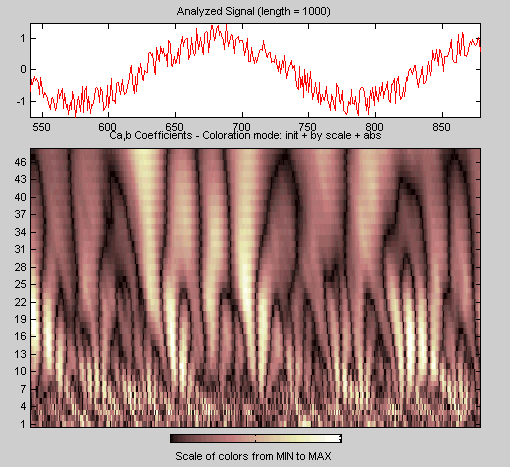
Как и при анализе командной строки на предыдущих страницах, можно изменить масштаб или анализирующий вейвлет и повторить анализ. Для этого просто отредактируйте необходимые поля и нажмите кнопку «Анализ».
Просмотр нормальных или абсолютных коэффициентов.
Инструмент Continuous Vavelet 1-D позволяет выводить на график либо абсолютные значения вейвлет-коэффициентов, либо сами коэффициенты.
В более общем случае окрашивание коэффициентов может быть выполнено несколькими различными способами. Дополнительные сведения о режиме окраски см. в разделе Управление режимом окраски.
Выберите один из абсолютных или обычных режимов в меню Режим окраски (Coloration Mode). В обычных режимах цвета масштабируются между минимальным и максимальным коэффициентами. В абсолютных режимах цвета масштабируются между нулем и максимальным абсолютным значением коэффициентов.