Представление сигнала в конкретном базисе включает в себя поиск уникального набора коэффициентов расширения в этом базисе. Хотя существует много преимуществ представления сигнала в базисе, в частности ортогональном базисе, есть и недостатки.
Способность базиса обеспечивать разреженное представление зависит от того, насколько хорошо характеристики сигнала соответствуют характеристикам базисных векторов. Например, гладкие непрерывные сигналы редко представлены в базисе Фурье, в то время как импульсы отсутствуют. Однако вейвлет-базис не эффективен для представления сигнала, преобразование Фурье которого имеет узкую высокочастотную поддержку.
Реальные сигналы часто содержат признаки, которые запрещают разреженное представление в любой отдельно взятой основе. Для этих сигналов требуется возможность выбора векторов из набора, не ограниченного одним базисом. Поскольку необходимо обеспечить возможность представления каждого вектора в пространстве, выбранный словарь векторов должен охватывать пространство. Однако, поскольку набор не ограничен одним базисом, словарь не является линейно независимым.
Поскольку векторы в словаре не являются линейно независимым набором, представление сигнала в словаре не является уникальным. Однако, создав избыточный словарь, можно расширить свой сигнал в набор векторов, которые адаптируются к частотно-временным или масштабным характеристикам вашего сигнала. Вы можете свободно создавать словарь, состоящий из объединения нескольких баз. Например, можно сформировать базис для пространства квадратно-интегрируемых функций, состоящих из вейвлет-пакетного базиса и локального косинусного базиса. Вейвлет-пакетный базис хорошо адаптирован к сигналам с различным поведением в различных частотных интервалах. Локальная косинусная основа хорошо адаптирована к сигналам с различным поведением в различных временных интервалах. Возможность выбора векторов из каждого из этих оснований значительно увеличивает вашу способность к скудному представлению сигналов с различными характеристиками.
Определите словарь как набор элементарных строительных блоков единичной нормы для сигнального пространства. Эти векторы единичной нормы называются атомами. Если атомы словаря охватывают все сигнальное пространство, словарь является полным.
Если атомы словаря образуют линейно-зависимое множество, словарь является избыточным. В большинстве приложений поиска совпадений словарь является полным и избыточным.
Пусть {øk} обозначает атомы словаря. Предположим, что словарь является полным и избыточным. Нет уникального способа представить сигнал из пространства в виде линейной комбинации атомов.
Важный вопрос заключается в том, существует ли наилучший способ. Интуитивно удовлетворительный способ выбора наилучшего представления состоит в том, чтобы выбрать фк, дающий наибольшие внутренние произведения (в абсолютном значении) с сигналом. Например, лучшим одиночным фk является
|
который для атома единичной нормы является величиной скалярной проекции на подпространство, охватываемое
Главная проблема в поиске совпадений заключается в том, как выбрать оптимальное М-образное расширение вашего сигнала в словаре.
Пусть для обозначения словаря атомов используется матрица N-by-M с M > N. Если полные, избыточные словарные формы структура для пространства сигнала, Вы можете получить минимальный содействующий вектор расширения нормы L2 при помощи оператора структуры.
Однако вектор коэффициентов, возвращаемый оператором кадра, не сохраняет разреженность. Если сигнал является разреженным в словаре, коэффициенты расширения, полученные с помощью канонического оператора кадра, обычно не отражают эту разреженность. Разреженность вашего сигнала в словаре - это черта, которую вы обычно хотите сохранить. Поиск соответствия непосредственно касается сохранения разреженности.
Поиск соответствия - жадный алгоритм, который вычисляет наилучшее нелинейное приближение к сигналу в полном, избыточном словаре. Поиск совпадения строит последовательность разреженных приближений к сигналу ступенчато. Пусть Start= {øk} обозначает словарь атомов единичной нормы. Пусть это твой сигнал.
Начать с определения R0f = f
Начните поиск совпадения, выбрав атом из словаря, который максимизирует абсолютное значение внутреннего произведения с R0f = f. Обозначим этот атом с помощью фр.
Сформируйте остаточную R1f путем вычитания ортогональной проекции R0f на пространство, охватываемое
Выполните итерацию повторением шагов 2 и 3 по остатку.
Остановите алгоритм при достижении определенного критерия остановки.
В неоргональном (или базовом) поиске совпадения атомы словаря не являются взаимно ортогональными векторами. Следовательно, вычитание последующих остатков из предыдущего может вводить компоненты, которые не ортогональны диапазону ранее включенных атомов.
Чтобы проиллюстрировать это, рассмотрим следующий пример. Пример не предназначен для представления рабочего алгоритма поиска соответствия.
Рассмотрим следующий словарь для евклидова 2-пространства. Этот словарь представляет собой фрейм равной нормы.
Предположим, что у вас есть следующий сигнал.
Следующий рисунок иллюстрирует этот пример. Атомы словаря выделены красным цветом. Вектор сигнала имеет синий цвет.
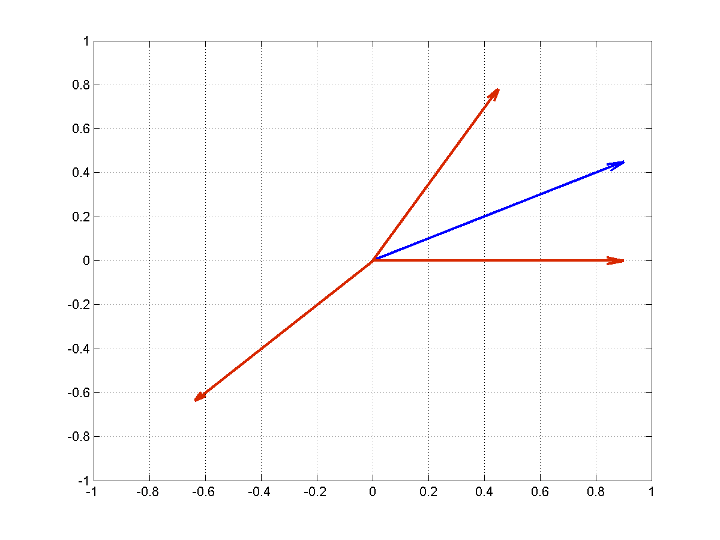
Создайте этот словарь и сигнал в MATLAB ®.
dictionary = [1 0; 1/2 sqrt(3)/2; -1/sqrt(2) -1/sqrt(2)]'; x = [1 1/2]';
Вычислите внутренние (скалярные) произведения между атомами сигнала и словаря.
scalarproducts = dictionary'*x;
Наибольшее скалярное произведение в абсолютном значении происходит между сигналом и [-1/sqrt(2); -1/sqrt(2)]. Это ясно, потому что угол между двумя векторами составляет почти δ радиан.
Сформировать остаток путем вычитания ортогональной проекции сигнала на [-1/sqrt(2); -1/sqrt(2)] от сигнала. Затем вычислите внутренние произведения остатка (нового сигнала) с оставшимися атомами словаря. Включать не обязательно [-1/sqrt(2); -1/sqrt(2)] потому что остаток ортогональен этому вектору путем построения.
residual = x-scalarproducts(3)*dictionary(:,3); scalarproducts = dictionary(:,1:2)'*residual;
Наибольшее скалярное произведение в абсолютном значении получается с помощью [1;0]. Лучшие два атома в словаре из двух итераций [-1/sqrt(2); -1/sqrt(2)] и [1;0]. Если выполнить итерацию по остатку, то будет видно, что выход больше не ортогональен первому выбранному атому. Другими словами, алгоритм ввел компонент, который не ортогональен диапазону первого выбранного атома. Этот факт и связанные с ним осложнения сходимости утверждают в пользу ортогонального совпадения (OMP).
В поиске ортогонального совпадения (OMP) остаток всегда ортогональен диапазону уже выбранных атомов. Это приводит к сходимости для d-мерного вектора после максимум d шагов.
Концептуально это можно сделать, используя Gram-Schmidt для создания ортонормированного набора атомов. С помощью ортонормированного набора атомов можно увидеть, что для d-мерного вектора можно найти не более d ортогональных направлений.
Алгоритм OMP:
Обозначьте сигнал с помощью f. Инициализируйте остаточный R0f = f.
Выберите атом, который максимизирует абсолютное значение внутреннего продукта с R0f = f. Обозначим этот атом по фр.
Сформуйте матрицу в виде предварительно выбранных атомов в качестве столбцов. Определите оператор ортогональной проекции на пролет колонн, входящих в Start.
Примените оператор ортогональной проекции к остатку.
Обновите остаток.
P) Rmf
Я - матрица тождественности.
Поиск ортогонального согласования гарантирует, что компоненты в диапазоне ранее выбранных атомов не будут введены на последующих этапах.
Это может быть вычислительно эффективным, чтобы смягчить критерий, что выбранный атом максимизирует абсолютное значение внутреннего продукта до менее строгого.
Это известно как слабое совпадение преследования.