В этом разделе рассматриваются функции дискретного стационарного вейвлет 2-D анализа с помощью программного обеспечения Wavelet Toolbox™.
| Имя функции | Цель |
|---|---|
Разложение |
| Имя функции | Цель |
|---|---|
Реконструкция |
Структура стационарного вейвлет-разложения более прослеживаема, чем вейвлет-структура. Таким образом, утилиты, полезные для случая вейвлета, не являются необходимыми для стационарного вейвлет-преобразования (SWT).
В этом разделе вы научитесь
Загрузить изображение
Анализ изображения
Выполнение одноуровневых и многоуровневых декомпозиций и реконструкций изображений (только в командной строке)
обличить изображение
В этом примере мы покажем, как можно использовать 2-D стационарный вейвлет-анализ для обличения изображения.
Примечание
Вместо использования image(I) для визуализации изображения I, мы используем image(wcodemat(I)), которая отображает масштабированную версию I приводя к более четкому представлению деталей и приближений (см. wcodemat справочная страница).
Этот пример включает изображение, содержащее шум.
Загрузите изображение.
В подсказке MATLAB ® введите
load noiswom whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
Для SWT, если декомпозиция на уровне k требуется, 2^k должны равномерно разделяться на size(X,1) и size(X,2). Если исходное изображение имеет неправильный размер, можно использовать функцию wextend для его удлинения.
Выполните одноуровневую стационарную вейвлет-декомпозицию.
Выполните одноуровневую декомпозицию изображения с помощью db1 вейвлет. Напечатать
[swa,swh,swv,swd] = swt2(X,1,'db1');
Это генерирует матрицы коэффициентов аппроксимации первого уровня (swa) и горизонтальные, вертикальные и диагональные детали (swh, swv, и swdсоответственно). Оба имеют размер - размер изображения. Напечатать
whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
swa | 96x96 | 73728 | double array |
swh | 96x96 | 73728 | double array |
swv | 96x96 | 73728 | double array |
swd | 96x96 | 73728 | double array |
Отображение коэффициентов аппроксимации и подробных данных.
Для отображения коэффициентов аппроксимации и деталей на уровне 1 введите
map = pink(size(map,1)); colormap(map)
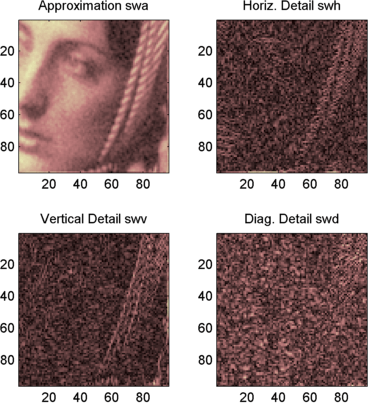
subplot(2,2,1), image(wcodemat(swa,192));
title('Approximation swa')
subplot(2,2,2), image(wcodemat(swh,192));
title('Horiz. Detail swh')
subplot(2,2,3), image(wcodemat(swv,192));
title('Vertical Detail swv')
subplot(2,2,4), image(wcodemat(swd,192));
title('Diag. Detail swd');
Регенерировать изображение с помощью обратного стационарного вейвлет-преобразования.
Чтобы найти обратное преобразование, введите
A0 = iswt2(swa,swh,swv,swd,'db1');
Чтобы проверить идеальную реконструкцию, введите
err = max(max(abs(X-A0)))
err =
1.1369e-13
Построение и отображение аппроксимации и деталей из коэффициентов.
Для построения аппроксимации и деталей уровня 1 (A1, H1, V1 и D1) из коэффициентов swa, swh, swv и swd, тип
nulcfs = zeros(size(swa)); A1 = iswt2(swa,nulcfs,nulcfs,nulcfs,'db1'); H1 = iswt2(nulcfs,swh,nulcfs,nulcfs,'db1'); V1 = iswt2(nulcfs,nulcfs,swv,nulcfs,'db1'); D1 = iswt2(nulcfs,nulcfs,nulcfs,swd,'db1');
Для просмотра аппроксимации и подробных данных на уровне 1 введите
colormap(map)
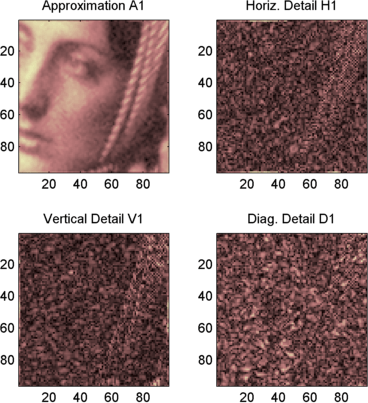
subplot(2,2,1), image(wcodemat(A1,192));
title('Approximation A1')
subplot(2,2,2), image(wcodemat(H1,192));
title('Horiz. Detail H1')
subplot(2,2,3), image(wcodemat(V1,192));
title('Vertical Detail V1')
subplot(2,2,4), image(wcodemat(D1,192));
title('Diag. Detail D1')
Выполните многоуровневую стационарную вейвлет-декомпозицию.
Для выполнения декомпозиции на уровне 3 изображения (снова с помощью db1 вейвлет), тип
[swa,swh,swv,swd] = swt2(X,3,'db1');
Это генерирует коэффициенты аппроксимаций на уровнях 1, 2 и 3 (swa) и коэффициенты деталей (swh, swv и swd). Обратите внимание, что матрицы swa(:,:,i), swh(:,:,i), swv(:,:,i), и swd(:,:,i) для данного уровня i имеют размер - размер изображения. Напечатать
clear A0 A1 D1 H1 V1 err nulcfs whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
swa | 96x96x3 | 221184 | double array |
swh | 96x96x3 | 221184 | double array |
swv | 96x96x3 | 221184 | double array |
swd | 96x96x3 | 221184 | double array |
Отображение коэффициентов аппроксимаций и деталей.
Для отображения коэффициентов аппроксимаций и деталей введите
colormap(map)
kp = 0;
for i = 1:3
subplot(3,4,kp+1), image(wcodemat(swa(:,:,i),192));
title(['Approx. cfs level ',num2str(i)])
subplot(3,4,kp+2), image(wcodemat(swh(:,:,i),192));
title(['Horiz. Det. cfs level ',num2str(i)])
subplot(3,4,kp+3), image(wcodemat(swv(:,:,i),192));
title(['Vert. Det. cfs level ',num2str(i)])
subplot(3,4,kp+4), image(wcodemat(swd(:,:,i),192));
title(['Diag. Det. cfs level ',num2str(i)])
kp = kp + 4;
end
Реконструировать аппроксимацию на уровне 3 и детали из коэффициентов.
Для восстановления аппроксимации на уровне 3 введите
mzero = zeros(size(swd)); A = mzero; A(:,:,3) = iswt2(swa,mzero,mzero,mzero,'db1');
Для восстановления подробных данных на уровнях 1, 2 и 3 введите
H = mzero; V = mzero;
D = mzero;
for i = 1:3
swcfs = mzero; swcfs(:,:,i) = swh(:,:,i);
H(:,:,i) = iswt2(mzero,swcfs,mzero,mzero,'db1');
swcfs = mzero; swcfs(:,:,i) = swv(:,:,i);
V(:,:,i) = iswt2(mzero,mzero,swcfs,mzero,'db1');
swcfs = mzero; swcfs(:,:,i) = swd(:,:,i);
D(:,:,i) = iswt2(mzero,mzero,mzero,swcfs,'db1');
end
Реконструируйте и отобразите аппроксимации на уровнях 1, 2 из аппроксимации на уровне 3 и детали на уровнях 1, 2 и 3.
Для восстановления аппроксимаций на уровнях 2 и 3 введите
A(:,:,2) = A(:,:,3) + H(:,:,3) + V(:,:,3) + D(:,:,3); A(:,:,1) = A(:,:,2) + H(:,:,2) + V(:,:,2) + D(:,:,2);
Для отображения аппроксимаций и подробных данных на уровнях 1, 2 и 3 введите
colormap(map)
kp = 0;
for i = 1:3
subplot(3,4,kp+1), image(wcodemat(A(:,:,i),192));
title(['Approx. level ',num2str(i)])
subplot(3,4,kp+2), image(wcodemat(H(:,:,i),192));
title(['Horiz. Det. level ',num2str(i)])
subplot(3,4,kp+3), image(wcodemat(V(:,:,i),192));
title(['Vert. Det. level ',num2str(i)])
subplot(3,4,kp+4), image(wcodemat(D(:,:,i),192));
title(['Diag. Det. level ',num2str(i)])
kp = kp + 4;
end
Удалите шум, установив пороговое значение.
Чтобы скрыть изображение, используйте пороговое значение, которое мы находим с помощью инструмента приложения Wavelet Analyzer (см. следующий раздел), используйте wthresh чтобы выполнить фактическое пороговое значение коэффициентов детализации, а затем используйте команду iswt2 команда на получение засекреченного изображения.
thr = 44.5; sorh = 's'; dswh = wthresh(swh,sorh,thr); dswv = wthresh(swv,sorh,thr); dswd = wthresh(swd,sorh,thr); clean = iswt2(swa,dswh,dswv,dswd,'db1');
Чтобы отобразить как исходное, так и обозначенное изображение, введите
colormap(map)
subplot(1,2,1), image(wcodemat(X,192));
title('Original image')
subplot(1,2,2), image(wcodemat(clean,192));
title('denoised image')

Второй синтаксис может использоваться для swt2 и iswt2 функции, дающие те же результаты:
lev= 4; swc = swt2(X,lev,'db1'); swcden = swc; swcden(:,:,1:end-1) = wthresh(swcden(:,:,1:end-1),sorh,thr); clean = iswt2(swcden,'db1');
Тот же график можно получить с помощью команд графика на шаге 9 выше.
В этом разделе мы исследуем стратегию обличения изображений, основанную на 2-D стационарном вейвлет-анализе с помощью приложения вейвлет-анализатора. Основная идея состоит в том, чтобы усреднить множество несколько различных дискретных вейвлет-анализов.
Запустите инструмент Denoising 2-D стационарного вейвлет-преобразования.
В приглашении MATLAB введите waveletAnalyzer.
Появится вейвлет-анализатор:
Выберите пункт меню SWT Denoising 2-D.
Загрузить данные.
В командной строке MATLAB введите
load noiswom
X переменная. Нажмите кнопку ОК, чтобы импортировать изображение.Выполните декомпозицию стационарного вейвлета.
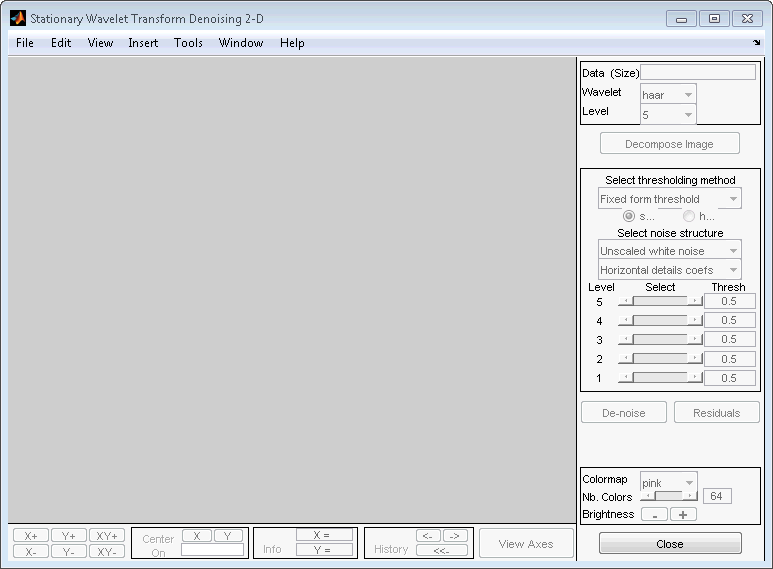
Выберите haar вейвлет в меню Вейвлет, выберите 4 в меню Уровень, а затем нажмите кнопку Разложить изображение.
Инструмент отображает гистограммы коэффициентов детализации стационарного вейвлета изображения в левой части окна. Эти гистограммы организованы следующим образом:
Снизу для уровня 1 до верха для уровня 4
Слева горизонтальные коэффициенты, посередине диагональные коэффициенты и справа вертикальные коэффициенты
Осквернение изображения с помощью стационарного вейвлет-преобразования.
Несмотря на то, что имеется ряд опций для точной настройки алгоритма деноизирования, мы примем значения по умолчанию мягкого порогового значения фиксированной формы и нескрупулезного белого шума. Ползунки, расположенные справа от окна, управляют зависящими от уровня порогами, обозначенными пунктирными линиями, проходящими вертикально через гистограммы коэффициентов слева от окна. Нажмите кнопку Denoise.
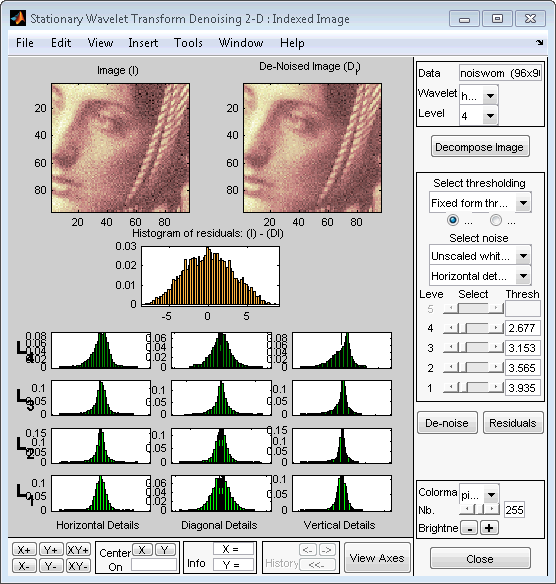
Результат, похоже, перегружен, а выбранные пороги слишком агрессивны. Тем не менее, гистограмма остатков довольно хороша, поскольку близка к гауссову распределению, которое является шумом, введенным для получения анализируемого изображения noiswom.mat из фрагмента исходного изображения woman.mat.
Выбор метода пороговой обработки.
В меню Выбор метода пороговой обработки выберите позицию «Штрафовать». Соответствующее значение по умолчанию для режима пороговой обработки автоматически устанавливается равным hard; принять его. Используйте ползунок «Sparsity» для настройки порогового значения, близкого к 45.5, а затем нажмите кнопку «Denoise».
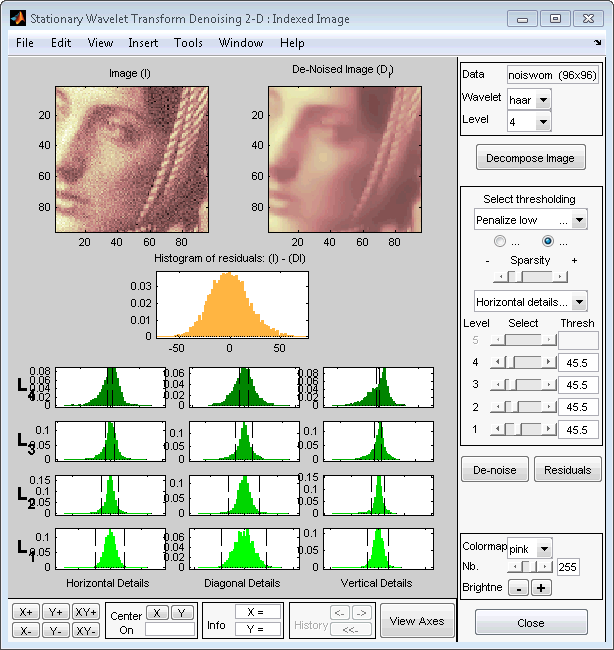
Результат вполне удовлетворительный, хотя улучшить его можно незначительно.
Выберите sym6 вейвлет и нажмите кнопку «Разложить изображение». Используйте ползунок «Sparsity» для настройки порогового значения, близкого к 40.44, а затем нажмите кнопку «Denoise».
Инструмент позволяет сохранить изображение с обозначением denoised на диск. Панель инструментов создает MAT-файл в текущей папке с выбранным именем.
Для сохранения запрещенного изображения из текущего процесса обнаружения используйте меню File > Save denoised Image. Появится диалоговое окно, в котором можно указать папку и имя файла для хранения изображения. Введите имя dnoiswom. После сохранения данных изображения в файл dnoiswom.mat, загрузите переменные в рабочую область:
load dnoiswom whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 96x96 | 73728 | double array |
map | 255x3 | 6120 | double array |
valTHR | 3x4 | 96 | double array |
wname | 1x4 | 8 | char array |
Обесцененное изображение X и map - цветовая карта. Кроме того, имеются параметры процесса обессоливания. Имя вейвлета содержится в wnameи пороговые значения, зависящие от уровня, кодируются в valTHR. Переменная valTHR имеет четыре столбца (уровень разложения) и три строки (по одной для каждой ориентации детализации).