Дискретное стационарное 2-D вейвлет-преобразование
[ возвращает коэффициенты аппроксимации A,H,V,D] = swt2(X,N,wname)A и коэффициенты детализации по горизонтали, вертикали и диагонали H, V, и Dсоответственно стационарной 2-D вейвлет-декомпозиции изображения X на уровне N использование вейвлета wname.
Примечание
swt2 использует периодическое расширение.
swt2 использует арифметику двойной точности внутри и возвращает матрицы коэффициентов двойной точности. swt2 предупреждает о потере точности при преобразовании в двойное значение.
swc = swt2(___)swc.
Загрузка и отображение изображения.
load woman imagesc(X) colormap(map) title('Original')
Выполнить стационарную вейвлет-декомпозицию изображения на уровне 2 с помощью db6.
[ca,chd,cvd,cdd] = swt2(X,2,'db6');Извлеките из разложения аппроксимацию уровня 1 и уровня 2 и коэффициенты детализации.
A1 = wcodemat(ca(:,:,1),255); H1 = wcodemat(chd(:,:,1),255); V1 = wcodemat(cvd(:,:,1),255); D1 = wcodemat(cdd(:,:,1),255); A2 = wcodemat(ca(:,:,2),255); H2 = wcodemat(chd(:,:,2),255); V2 = wcodemat(cvd(:,:,2),255); D2 = wcodemat(cdd(:,:,2),255);
Отображение коэффициентов аппроксимации и детализации с двух уровней.
subplot(2,2,1) imagesc(A1) title('Approximation Coef. of Level 1') subplot(2,2,2) imagesc(H1) title('Horizontal Detail Coef. of Level 1') subplot(2,2,3) imagesc(V1) title('Vertical Detail Coef. of Level 1') subplot(2,2,4) imagesc(D1) title('Diagonal Detail Coef. of Level 1')
subplot(2,2,1) imagesc(A2) title('Approximation Coef. of Level 2') subplot(2,2,2) imagesc(H2) title('Horizontal Detail Coef. of Level 2') subplot(2,2,3) imagesc(V2) title('Vertical Detail Coef. of Level 2') subplot(2,2,4) imagesc(D2) title('Diagonal Detail Coef. of Level 2')
В этом примере показано, как получить одноуровневую и многоуровневую стационарную вейвлет-декомпозицию изображения RGB.
Загрузите и просмотрите изображение RGB. Изображение является 3-D массивом типа uint8. С тех пор swt2 требует, чтобы первый и второй размеры были разделены на степень 2, извлекают часть изображения.
imdata = imread('ngc6543a.jpg'); x = imdata(1:512,1:512,:); image(x) title('RGB Image')
Получение стационарной вейвлет-декомпозиции изображения уровня 4 с помощью db4 вейвлет. Возвращает коэффициенты аппроксимации. Обратите внимание на размеры массива коэффициентов.
[a,~,~,~] = swt2(x,4,'db4');
size(a)ans = 1×4
512 512 3 4
Все коэффициенты имеют тип double. В массиве RGB типа doubleкаждый компонент цвета имеет значение от 0 до 1. Масштабируйте коэффициенты аппроксимации уровня 2 до значений от 0 до 1 и просмотрите результат.
a2 = a(:,:,:,2);
a2 = (a2-min(a2(:)))/(max(a2(:))-min(a2(:)));
image(a2)
title('Level 2 Approximation')
Получение одноуровневой стационарной вейвлет-декомпозиции изображения с помощью db4 вейвлет. Возвращает коэффициенты аппроксимации. В одноуровневой декомпозиции изображения RGB третье измерение является одиночным.
[a,~,~,~] = swt2(x,1,'db4');
size(a)ans = 1×4
512 512 1 3
Просмотрите коэффициенты аппроксимации. Предотвращение ошибок при использовании image, сжать массив коэффициентов аппроксимации, чтобы удалить одиночную размерность.
a2 = squeeze(a);
a2 = (a2-min(a(:)))/(max(a(:))-min(a(:)));
image(a2)
title('Approximation')
Для изображений алгоритм стационарного вейвлет-преобразования (SWT), аналогичный одномерному случаю, возможен для двумерных вейвлетов и функций масштабирования, полученных из одномерных функций тензорным произведением. Такой вид двумерного SWT приводит к разложению коэффициентов аппроксимации на уровне j на четыре составляющие: аппроксимация на уровне j + 1, а детали в трёх ориентациях (горизонтальной, вертикальной и диагональной).
Эта диаграмма описывает базовый шаг разложения для изображений.
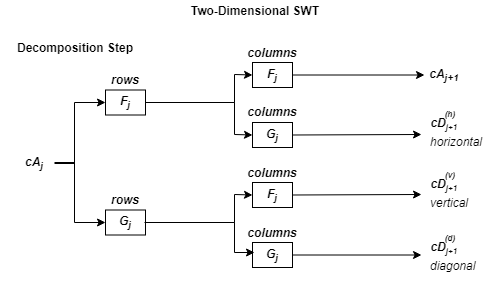
где
- Свернуть строки записи с фильтром X.
- Свернуть столбцы записи с фильтром X.
Инициализация
cA0 = s
F0 = LoD
G0 = HiD
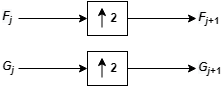
где
обозначает upsample.
Обратите внимание, что size(cAj) = size(cDj(h)) = size(cDj(v)) = size(cDj(d)) = s, где s равно размеру анализируемого изображения.
[1] Насон, Г. П. и Б. В. Сильверман. «Стационарное вейвлет-преобразование и некоторые статистические приложения». В «Вейвлетах и статистике» под редакцией Анестиса Антониадиса и Жоржа Оппенгейма, 103: 281-99. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_17.
[2] Койфман, Р. Р. и Д. Л. Донохо. «Перевод-инвариантное снятие шума». В «Вейвлетах и статистике» под редакцией Анестиса Антониадиса и Жоржа Оппенгейма 103: 125-50. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_9.
[3] Pesquet, J.-C., H. Krim и H. Carfantan. «Инвариантные во времени ортонормированные вейвлет-представления». Транзакции IEEE по обработке сигналов 44, № 8 (август 1996 года): 1964-70. https://doi.org/10.1109/78.533717.