Оценка вейвлет-деноизирующей и непараметрической функций

Вейвлет Toolbox™ обеспечивает ряд функций для оценки неизвестной функции (сигнала или изображения) в шуме. Эти функции можно использовать для обессоливания сигналов и в качестве метода оценки непараметрических функций.

Самая общая 1-D модель для этого

s (n) = f (n) + starte (n)

где n = 0,1,2,...N-1. E (n) - гауссовы случайные величины, распределенные как N (0,1). Дисперсию (n) (e) составляет (2).

На практике s (n) часто является дискретным сигналом времени с равными шагами времени, искаженными аддитивным шумом, и вы пытаетесь восстановить этот сигнал.

В более общем случае, вы можете рассматривать s (n) как N-мерный случайный вектор

$(\begin{matrix} f (0) + starte \\ (0) f (1) \\ + starte (1) \\ f \\ ( \\ 2) + (2)... \end{matrix} f \begin{matrix} (N - \\ 1) \\ + starte \\ ( \\ N \\ - 1)) \end{matrix} = \begin{matrix} (f (0 \\ ) f ( \\ 1) f \\ ( \\ 2 \\ ) \\ . . . f ( \end{matrix} N$ − 1)) + (

В этом общем контексте связь между отрицанием и регрессией очевидна.

Можно заменить N-by-1 случайный вектор на N-by-M случайные матрицы, чтобы получить задачу восстановления изображения, поврежденного аддитивным шумом.

Можно получить 1-D пример этой модели со следующим кодом.

load cuspamax;
y = cuspamax+0.5*randn(size(cuspamax));
plot(y); hold on;
plot(cuspamax,'r','linewidth',2);
axis tight;
legend('f(n)+\sigma e(n)','f(n)', 'Location', 'NorthWest');

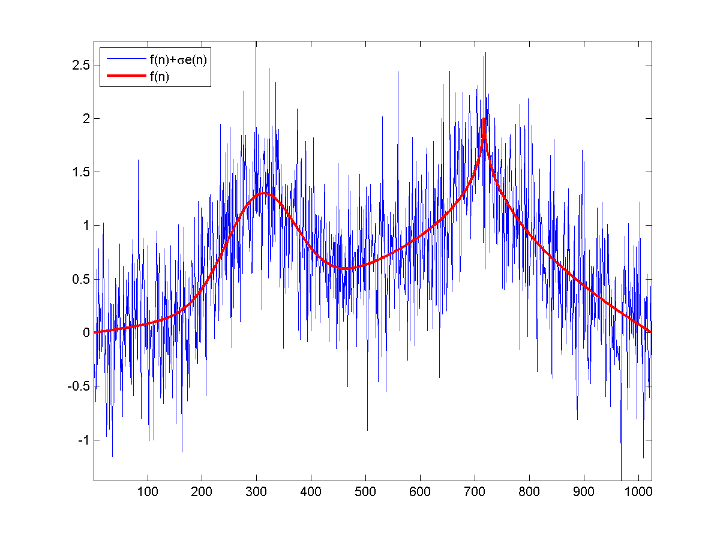
Для широкого класса функций (сигналы, изображения), которые обладают определенными свойствами плавности, вейвлет-методы оптимальны или почти оптимальны для восстановления функции.

В частности, способ эффективен для семейств функций f, которые имеют только несколько ненулевых вейвлет-коэффициентов. Эти функции имеют разреженное вейвлет представление. Например, гладкая функция почти везде, с несколькими резкими изменениями, имеет такое свойство.

Общий вейвлет-основанный способ для деноизирования и непараметрической оценки функции заключается в преобразовании данных в вейвлет-область, пороговом значении вейвлет-коэффициентов и инвертировании преобразования.

Эти шаги можно суммировать следующим образом:

Разложиться
Выберите вейвлет и уровень N. Вычислите вейвлет-разложение сигнала s до уровня N.
Коэффициенты детализации порога
Для каждого уровня от 1 до N пороговые коэффициенты детализации.
Восстановить
Вычисляют вейвлет-реконструкцию с использованием исходных коэффициентов аппроксимации уровня N и модифицированных коэффициентов детализации уровней от 1 до N.

Методы деноизирования

Инструментарий Wavelet Toolbox поддерживает ряд деноизлучающих методов. Четыре денойзинговых метода реализованы в thselect. Каждый метод соответствует tptr параметр в команде

thr = thselect(y,tptr)

которое возвращает пороговое значение.

Выбор	Метод деноизирования
`'rigrsure'`	Выбор с использованием принципа объективной оценки риска (SURE) Stein
`'sqtwolog'`	Фиксированный (универсальный) порог формы, равный $\sqrt{2ln (N}$ ) с N длиной сигнала.
`'heursure'`	Выбор с использованием комбинации первых двух опций
`'minimaxi'`	Выбор с использованием принципа minimax

Выбор 'rigrsure' использует для мягкой оценки порога правило выбора порога, основанное на несмещенной оценке риска Штейна (квадратичная функция потерь). Вы получаете оценку риска для конкретного порогового значения т. Минимизация рисков в t дает выбор порогового значения.
Выбор 'sqtwolog' использует фиксированный порог формы, дающий производительность minimax, умноженную на небольшой коэффициент, пропорциональный log (length (s)).
Выбор 'heursure' представляет собой смесь двух предыдущих вариантов. В результате, если отношение сигнал/шум очень мало, оценка SURE очень шумная. Таким образом, если такая ситуация обнаружена, используется порог фиксированной формы.
Выбор 'minimaxi' использует фиксированный порог, выбранный для получения производительности minimax для среднеквадратической ошибки против идеальной процедуры. Принцип minimax используется в статистике для разработки оценщиков. Так как деноизированный сигнал может быть ассимилирован в блок оценки неизвестной функции регрессии, блок оценки minimax является опцией, которая реализует минимум, по заданному набору функций, максимальной среднеквадратической ошибки.

Следующий пример показывает способы деноизирования для вектора 1000 на 1 N (0,1). Сигнал здесь

$f (n) + e (n) e (n) ~ N$ (0,1)

с f (n) = 0.

rng default;
sig = randn(1e3,1);
thr_rigrsure = thselect(sig,'rigrsure')
thr_univthresh = thselect(sig,'sqtwolog')
thr_heursure = thselect(sig,'heursure')
thr_minimaxi = thselect(sig,'minimaxi')
histogram(sig);
h = findobj(gca,'Type','patch');
set(h,'FaceColor',[0.7 0.7 0.7],'EdgeColor','w');
hold on;
plot([thr_rigrsure thr_rigrsure], [0 300],'linewidth',2);
plot([thr_univthresh thr_univthresh], [0 300],'r','linewidth',2);
plot([thr_minimaxi thr_minimaxi], [0 300],'k','linewidth',2);
plot([-thr_rigrsure -thr_rigrsure], [0 300],'linewidth',2);
plot([-thr_univthresh -thr_univthresh], [0 300],'r','linewidth',2);
plot([-thr_minimaxi -thr_minimaxi], [0 300],'k','linewidth',2);

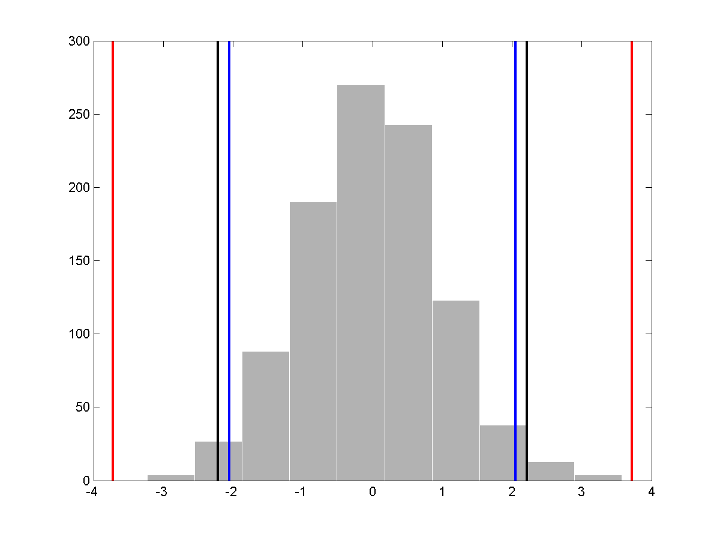
Для необъективной оценки риска Штайна (SURE) и минимальных пороговых значений сохраняется примерно 3% коэффициентов. В случае универсального порога все значения отклоняются.

Известно, что вектор коэффициентов детализации является наложением коэффициентов f и коэффициентов e, и что разложение e приводит к коэффициентам детализации, которые являются стандартными гауссовыми белыми шумами.

После использования thselect для определения порога можно задать пороговое значение для каждого уровня. Этот второй шаг можно выполнить с помощью wthcoef, непосредственно обрабатывая структуру вейвлет-разложения исходного сигнала s.

Мягкое или жесткое пороговое значение

Жесткое и мягкое пороговое значение является примером правил усадки. После определения порога необходимо решить, как применить этот порог к данным.

Простейшая схема - жесткое пороговое значение. Пусть T обозначает порог и x ваших данных. Жесткое пороговое значение:

$(x) \begin{array}{l} = & {x 'x | \\ \geqT0|x| \end{array}$ < T

Мягкое пороговое значение:

$start(x) \begin{array}{l} \end{array}$ ={x−Tx>T0|x|≤Tx+Tx<−T

Вы можете применить порог, используя жесткое или мягкое правило с wthresh.

y = linspace(-1,1,100);
thr = 0.4;
ythard = wthresh(y,'h',thr);
ytsoft = wthresh(y,'s',thr);
subplot(131);
plot(y); title('Original Data');
subplot(132);
plot(ythard,'*'); title('Hard Thresholding');
subplot(133);
plot(ytsoft,'*'); title('Soft Thresholding');

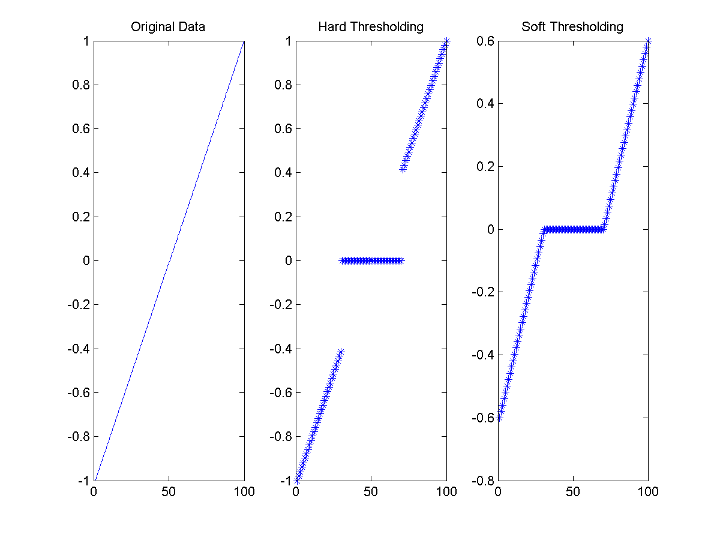
Работа с нескрупулезным шумом и небелым шумом

Обычно на практике базовая модель не может использоваться непосредственно. Мы рассмотрим здесь доступные варианты для решения проблем с отклонениями модели в основной функции денойзинга wdenoise.

Простейшее использование wdenoise является

sd = wdenoise(s)

который возвращает деноизированную версию sd исходного сигнала s получают с использованием настроек по умолчанию для параметров, включая вейвлет, способ деноизирования и мягкое или жесткое пороговое значение. Можно изменить любые настройки по умолчанию:

sd = wdenoise(s,n,'DenoisingMethod',tptr,'Wavelet',wav,...
     'ThresholdRule',sorh,'NoiseEstimate',scal)

который возвращает деноизированную версию sd исходного сигнала s полученные с использованием tptr СПОСОБ ДЕНОИЗИРОВАНИЯ. Другие необходимые параметры: sorh, scal, и wname. Параметр sorh задает пороговое значение коэффициентов детализации разложения на уровне n из s по вейвлету, вызываемому wav. Оставшийся параметр scal необходимо указать. Он соответствует способу оценки дисперсии шума в данных.

Выбор	Метод оценки шума
`'LevelIndependent'`	`'LevelIndependent'` оценивает дисперсию шума на основе вейвлет-коэффициентов с самым мелким масштабом (наивысшим разрешением).
`'LevelDependent'`	`'LevelDependent'` оценивает дисперсию шума на основе вейвлет-коэффициентов на каждом уровне разрешения.

Для более общей процедуры, wdencmp функция выполняет порогование вейвлет-коэффициентов как для деноизирования, так и для сжатия, при этом непосредственно обрабатывая 1-D и 2-D данные. Это позволяет определить собственную стратегию пороговой обработки, выбираемую в

 xd = wdencmp(opt,x,wav,n,thr,sorh,keepapp);

где

opt = 'gbl' и thr является положительным действительным числом для однородного порога.
opt = 'lvd' и thr является вектором для порога, зависящего от уровня.
keepapp = 1 для сохранения коэффициентов аппроксимации, как ранее и
keepapp = 0 для обеспечения возможности пороговой обработки коэффициентов аппроксимации.
x является сигналом, который должен быть денонсирован и wav, n, sorh те же, что и выше.

Вейвлет Денизинг в действии

Открыть сценарий в реальном времени

Мы начинаем примеры методов 1-D отрицания с первого примера, приписанного Донохо и Джонстоуну.

Блокирование порогов сигналов

Сначала установите отношение сигнал-шум (SNR) и задайте случайное начальное число.

sqrt_snr = 4;
init = 2055615866;

Генерировать исходный сигнал xref и шумная версия x путем добавления стандартного гауссова белого шума. Постройте график обоих сигналов.

[xref,x] = wnoise(1,11,sqrt_snr,init);
subplot(2,1,1)
plot(xref)
axis tight
title('Original Signal')
subplot(2,1,2)
plot(x)
axis tight
title('Noisy Signal')

Figure contains 2 axes. Axes 1 with title Original Signal contains an object of type line. Axes 2 with title Noisy Signal contains an object of type line.

Денуазировать шумный сигнал с использованием мягкого эвристического порогового значения SURE для коэффициентов детализации, полученных из вейвлет-разложения x с использованием sym8 вейвлет. Использовать настройки по умолчанию wdenoise для остальных параметров. Сравните с исходным сигналом.

xd = wdenoise(x,'Wavelet','sym8','DenoisingMethod','SURE','ThresholdRule','Soft');
figure
subplot(2,1,1)
plot(xref)
axis tight
title('Original Signal')
subplot(2,1,2)
plot(xd)
axis tight
title('Denoised Signal')

Figure contains 2 axes. Axes 1 with title Original Signal contains an object of type line. Axes 2 with title Denoised Signal contains an object of type line.

Поскольку только небольшое количество больших коэффициентов характеризует исходный сигнал, способ работает очень хорошо.

Деноизирование электрических сигналов

При подозрении на небелый шум пороговые значения должны быть масштабированы посредством оценки уровня шума. В качестве второго примера рассмотрим метод на сильно возмущенной части электрического сигнала.

Сначала загрузите электрический сигнал и выберите из него сегмент. Постройте график сегмента.

load leleccum
indx = 2000:3450;
x = leleccum(indx);
figure
plot(indx,x)
axis tight
title('Original Signal')

Figure contains an axes. The axes with title Original Signal contains an object of type line.

Denoise сигнал с помощью db3 вейвлет и трехуровневая вейвлет-декомпозиция и пороговое значение мягкой фиксированной формы. Чтобы справиться с небелым шумом, используйте оценку размера шума, зависящую от уровня. Сравните с исходным сигналом.

xd = wdenoise(x,3,'Wavelet','db3',...
    'DenoisingMethod','UniversalThreshold',...
    'ThresholdRule','Soft',...
    'NoiseEstimate','LevelDependent');
figure
subplot(2,1,1)
plot(indx,x)
axis tight
title('Original Signal')
subplot(2,1,2)
plot(indx,xd)
axis tight
title('Denoised Signal')

Figure contains 2 axes. Axes 1 with title Original Signal contains an object of type line. Axes 2 with title Denoised Signal contains an object of type line.

Результат довольно хороший, несмотря на временную неоднородность характера шума после и до начала отказа датчика в течение времени 2410.

Расширение до «Denoising»

Открыть сценарий в реальном времени

Способ обличения, описанный для 1-D случая, применим также к изображениям и хорошо применим к геометрическим изображениям. Прямой перевод модели 1-D

$s (i, j) = f (i, j) +$ starte (i, j)

где $e$ - белый гауссов шум с единичной дисперсией.

Процедура 2-D denoising имеет те же три шага и использует инструменты 2-D вейвлет вместо инструментов 1-D. Для выбора порогового значения prod(size(s)) используется вместо length(s) если используется фиксированный порог формы.

Обратите внимание, что за исключением «автоматического» 1-D denoising случай, 2-й denoising и сжатие выполняются, используя wdencmp. Чтобы проиллюстрировать 2-D отрицание, загрузите изображение и создайте его шумную версию. Для воспроизводимости задайте случайное начальное число.

init = 2055615866;
rng(init);
load woman
img = X;
imgNoisy = img + 15*randn(size(img));

Использовать ddencmp чтобы найти отрицательные значения. При этом используется порог фиксированной формы с оценкой уровня шума, пороговое значение является мягким и коэффициенты аппроксимации сохраняются.

[thr,sorh,keepapp] = ddencmp('den','wv',imgNoisy);
thr

thr = 107.9838

thr равно estimated_sigma*sqrt(log(prod(size(img)))).

Оскверните шумное изображение с помощью опции global threshold. Просмотрите результаты.

imgDenoised = wdencmp('gbl',imgNoisy,'sym4',2,thr,sorh,keepapp);
figure
colormap(pink(255))
sm = size(map,1);
subplot(2,2,1)
image(wcodemat(img,sm))
title('Original Image')
subplot(2,2,2)
image(wcodemat(imgNoisy,sm))
title('Noisy Image')
subplot(2,2,3)
image(wcodemat(imgDenoised,sm))
title('Denoised Image')

Figure contains 3 axes. Axes 1 with title Original Image contains an object of type image. Axes 2 with title Noisy Image contains an object of type image. Axes 3 with title Denoised Image contains an object of type image.

Обличенное изображение хорошо сравнивается с исходным изображением.

1-D Адаптивное пороговое значение вейвлет-дисперсии

Открыть сценарий в реальном времени

Идея состоит в том, чтобы определить уровень по уровням зависящих от времени пороговых значений, а затем увеличить способность стратегий денойзинга обрабатывать модели нестационарного дисперсионного шума.

Точнее, модель предполагает (как и ранее), что наблюдение равно интересному сигналу, наложенному на шум

$s (n) = f (n) +$ starte (n)

Но дисперсия шума может изменяться со временем. Существует несколько различных значений отклонений в нескольких временных интервалах. Значения, а также интервалы неизвестны.

Давайте сосредоточимся на проблеме оценки точек изменения или эквивалентных интервалов. Используемый алгоритм основан на оригинальной работе Марка Лавилле об обнаружении точек изменения с помощью динамического программирования (см. [Lav99] в Справках).

Давайте сформируем сигнал из регрессионной модели фиксированной конструкции с двумя точками изменения дисперсии шума, расположенными в положениях 200 и 600. Для воспроизводимости задайте случайное начальное число.

init = 2055615866;
rng(init);

x = wnoise(1,10);
bb = randn(1,length(x));
cp1 = 200;
cp2 = 600;
x = x+[bb(1:cp1),bb(cp1+1:cp2)/4,bb(cp2+1:end)];
plot(x)
title('Noisy Signal')

Figure contains an axes. The axes with title Noisy Signal contains an object of type line.

Целью этого примера является восстановление двух точек изменения из сигнала x.

Шаг 1. Восстановление шумного сигнала путем подавления аппроксимации. Сначала выполните одноуровневую вейвлет-декомпозицию с использованием db3 вейвлет. Затем реконструируйте деталь на уровне 1.

wname = 'db3';
lev = 1;
[c,l] = wavedec(x,lev,wname);
det = wrcoef('d',c,l,wname,1);
figure
plot(det)
title('Level 1 Detail')

Figure contains an axes. The axes with title Level 1 Detail contains an object of type line.

Восстановленная деталь на уровне 1, восстановленная на этой стадии, практически свободна от сигнала. Он фиксирует основные признаки шума с точки зрения обнаружения точек изменения, если интересная часть сигнала имеет разреженное вейвлет-представление. Чтобы удалить почти весь сигнал, мы заменим самые большие значения на средние.

Шаг 2. Чтобы удалить почти весь сигнал, замените 2% наибольших значений на среднее.

x = sort(abs(det));
v2p100 = x(fix(length(x)*0.98));
ind = find(abs(det)>v2p100);
det(ind) = mean(det);

Шаг 3. Используйте wvarchg для оценки точек изменения со следующими параметрами:

Минимальная задержка между двумя точками изменения равна d = 10.
Максимальное количество точек изменения - 5.

[cp_est,kopt,t_est] = wvarchg(det,5)

cp_est = 1×2

   259   611

kopt = 2

t_est = 6×6

        1024           0           0           0           0           0
         612        1024           0           0           0           0
         259         611        1024           0           0           0
         198         259         611        1024           0           0
         198         235         259         611        1024           0
         198         235         260         346         611        1024

Предлагаются две точки изменения и три интервала. Поскольку отклонения трех интервалов для шума очень различны, программа оптимизации легко обнаруживает правильную структуру. Расчетные точки изменения близки к истинным точкам изменения: 200 и 600.

Шаг 4. (Необязательно) Замените расчетные точки изменения.

Для 2 $\leq$ i ≤ 6, t_est(i,1:i-1) содержит i-1 моменты точек изменения отклонения, а с kopt - предлагаемое количество точек изменения, то

cp_est = t_est(kopt+1,1:kopt);

Расчетные точки изменения можно заменить вычислениями:

for k=1:5
    cp_New = t_est(k+1,1:k)
end

cp_New = 612

cp_New = 1×2

   259   611

cp_New = 1×3

   198   259   611

cp_New = 1×4

   198   235   259   611

cp_New = 1×5

   198   235   260   346   611

Измерения вейвлет-деноизирующего анализа

Следующие измерения и настройки полезны для анализа вейвлет-сигналов и изображений:

M S E - среднеквадратическая ошибка (MSE) - квадратичная норма разности между данными и аппроксимацией сигнала или изображения, деленная на количество элементов.
Максимальная ошибка - максимальное абсолютное квадратичное отклонение в приближении сигнала или изображения.
L2-Norm Ratio - отношение квадрата L2-norm сигнала или аппроксимации изображения к входному сигналу или изображению. Для изображений изображение изменяется в виде вектора столбца перед выполнением L2-norm
P S N R - Пиковое отношение сигнал/шум (PSNR) в децибелах. PSNR имеет значение только для данных, закодированных в терминах битов на выборку или битов на пиксель.
B P - отношение битов на пиксель (BPP), которое является отношением сжатия (Comp. ratio), умноженным на 8, предполагая один байт на пиксель (8 бит).
Comp Ratio - коэффициент сжатия, который представляет собой количество элементов в сжатом изображении, деленное на количество элементов в исходном изображении, выраженное в процентах.

Документация