В этом разделе демонстрируются возможности многомасштабного анализа основных компонентов, обеспечиваемого программным обеспечением Wavelet Toolbox™. Панель инструментов включает wmspca функция и приложение Wavelet Analyzer. В этом разделе описываются методы командной строки и приложения, а также информация о передаче информации о сигнале и параметрах между диском и приложением.
Целью многомасштабного PCA является восстановление, начиная с многомерного сигнала и используя простое представление на каждом уровне разрешения, упрощенного многомерного сигнала. Многомасштабные главные компоненты обобщают нормальное PCA многомерного сигнала, представленного в виде матрицы, путем выполнения PCA на матрицах деталей различных уровней одновременно. PCA также выполняется на матрице коэффициентов грубой аппроксимации в вейвлет-области, а также на окончательной реконструированной матрице. Выбирая количество сохраненных главных компонентов, можно восстанавливать интересные упрощенные сигналы.
Поскольку многомасштабный PCA можно выполнять либо из командной строки, либо с помощью приложения, в этом разделе содержатся подразделы, охватывающие каждый метод.
В этом примере используются шумные тестовые сигналы. В этом разделе вы:
Загрузите многомерный сигнал.
Выполнение простого многомасштабного PCA.
Отображение исходного и упрощенного сигналов.
Улучшите полученный результат, сохранив меньше основных компонентов.
Загрузите многомерный сигнал, набрав в подсказке MATLAB ®:
load ex4mwden whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
covar | 4x4 | 128 | double array |
x | 1024x4 | 32768 | double array |
x_orig | 1024x4 | 32768 | double array |
Данные, сохраненные в матрице x происходит от двух тестовых сигналов, Blocks и CharchSine, и от их суммы и разности, к которым добавился многомерный гауссов белый шум.
Выполнение простого многомасштабного PCA.
Многомасштабный PCA объединяет нецентрированный PCA на аппроксимациях и деталях в вейвлет-области и конечном PCA. На каждом уровне выбираются наиболее важные основные компоненты.
Сначала задайте вейвлет-параметры:
level= 5; wname = 'sym4';
Затем автоматически выберите количество сохраненных основных компонентов с помощью правила Кайзера, введя
npc = 'kais';
Наконец, выполните многомасштабное PCA:
[x_sim, qual, npc] = wmspca(x ,level, wname, npc);
Отображение исходных и упрощенных сигналов:
kp = 0;
for i = 1:4
subplot(4,2,kp+1), plot(x (:,i)); set(gca,'xtick',[]);
axis tight;
title(['Original signal ',num2str(i)])
subplot(4,2,kp+2), plot(x_sim(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Simplified signal ',num2str(i)])
kp = kp + 2;
end
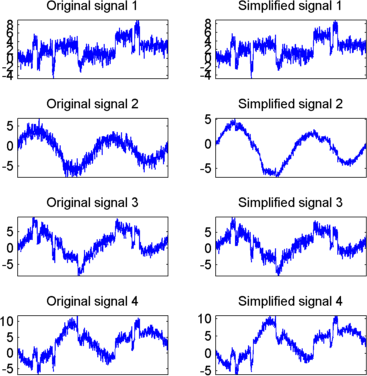
Результаты с точки зрения сжатия являются хорошими. Проценты, отражающие качество реконструкции столбцов, задаваемые относительными среднеквадратическими ошибками, близки к 100%.
qual qual = 98.0545 93.2807 97.1172 98.8603
Улучшите первый результат, сохранив меньше главных компонентов.
Результаты могут быть улучшены путем подавления шума, поскольку детали на уровнях 1-3 состоят по существу из шума с небольшими вкладами сигнала. Удаление шума приводит к грубому, но большому, денозирующему эффекту.
Выходной аргумент npc содержит количество сохраненных главных компонентов, выбранных по правилу Кайзера:
npc
npc =
1 1 1 1 1 2 2
Для d от 1 до 5, npc(d) - количество сохраненных нецентрированных основных компонентов (ПК) для получения подробной информации на уровне d. Количество сохраненных нецентрированных ПК для аппроксимаций на уровне 5 равно npc(6), и npc(7) - количество сохраненных ПК для окончательного PCA после вейвлет-реконструкции. Как и ожидалось, правило сохраняет два основных компонента, как для аппроксимаций PCA, так и для конечного PCA, но один главный компонент сохраняется для подробной информации на каждом уровне.
Чтобы подавить сведения на уровнях 1-3, обновите npc аргумент следующим образом:
npc(1:3) = zeros(1,3); npc npc = 0 0 0 1 1 2 2
Затем снова выполните многомасштабную PCA:
[x_sim, qual, npc] = wmspca(x, level, wname, npc);
Отображение исходного и окончательного упрощенных сигналов:
kp = 0;
for i = 1:4
subplot(4,2,kp+1), plot(x (:,i)); set(gca,'xtick',[]);
axis tight;
title(['Original signal ',num2str(i)]); set(gca,'xtick',[]);
axis tight;
subplot(4,2,kp+2), plot(x_sim(:,i)); set(gca,'xtick',[]);
axis tight;
title(['Simplified signal ',num2str(i)])
kp = kp + 2;
end
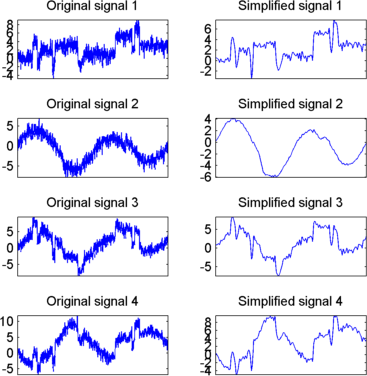
Как показано, результаты улучшаются.
В этом разделе рассматривается многомасштабный PCA с помощью приложения Wavelet Analyzer.
Откройте приложение Wavelet Analyzer, введя waveletAnalyzer в командной строке.
Щелкните Анализ мультимасштабных основных компонентов, чтобы открыть инструмент анализа мультимасштабных основных компонентов в приложении.
Загрузить данные.
В командной строке MATLAB введите
load ex4mwden
x переменная. Нажмите кнопку OK для импорта многомерного сигнала. Сигнал представляет собой матрицу, содержащую четыре столбца, где каждый столбец является сигналом, подлежащим упрощению.
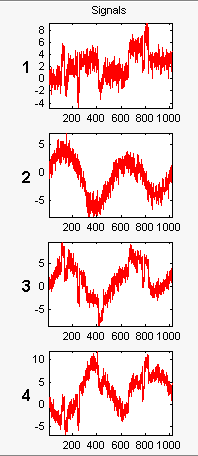
Эти сигналы являются шумными версиями из простых комбинаций двух исходных сигналов, Blocks и CharcSine и их суммы и разности, каждый с добавленным многомерным гауссовым белым шумом.
Выполните вейвлет-декомпозицию и диагонализацию каждой матрицы коэффициентов.
Используйте значения по умолчанию для вейвлета, режима расширения DWT и уровня разложения, а затем щелкните Разложить (Decompose) и Диагонализировать (Diagonalize). Инструмент отображает вейвлет-аппроксимацию и коэффициенты детализации разложения каждого сигнала в исходном базисе.
Чтобы получить более подробную информацию о новых базах, разрешенных для выполнения PCA для каждой шкалы, щелкните Дополнительно на адаптированной основе (More on Adapted Basis). На новом рисунке показаны соответствующие собственные векторы и собственные значения для матрицы коэффициентов детализации на уровне 1.

Можно изменить уровень или выбрать более грубые приближения или реконструированную матрицу для исследования различных оснований. По завершении нажмите кнопку Закрыть.
Выполнение простого многомасштабного PCA.
Исходные значения для PCA приводят к сохранению всех компонентов. Выбрать Kaiser в раскрывающемся списке Предоставить по умолчанию с помощью (Provide default using) и нажмите кнопку Применить (Apply).
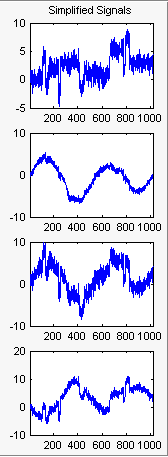
Результаты хороши с точки зрения сжатия.
Улучшите полученный результат, сохранив меньше основных компонентов.
Результаты могут быть улучшены путем подавления шума, потому что детали на уровнях 1-3 состоят по существу из шума с небольшими вкладами сигнала, как вы можете видеть, тщательно проверяя коэффициенты детализации. Удаление шума приводит к грубому, но большому, денозирующему эффекту.
Для D1, D2 и D3 выберите 0 как Nb. нецентрированного ПК и нажмите кнопку Применить.
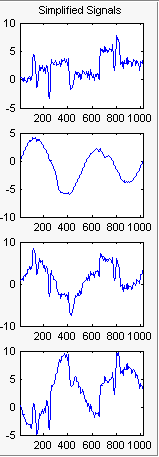
Результаты лучше, чем полученные ранее. Первый сигнал, который является нерегулярным, все еще правильно восстанавливается, в то время как второй сигнал, который является более регулярным, после этой второй ступени PCA денонсируется лучше. Дополнительную информацию можно получить, щелкнув Остатки (Residuals).
Инструмент «Анализ многомасштабных основных компонентов» позволяет сохранять упрощенные сигналы на диск. Панель инструментов создает MAT-файл в текущей папке с выбранным именем.
Для сохранения упрощенных сигналов из предыдущего раздела:
Выберите «Файл» > «Сохранить упрощенные сигналы».
Выберите «Сохранить упрощенные сигналы и параметры». Появится диалоговое окно, в котором можно указать папку и имя файла для хранения сигнала.
Введите имя s_ex4mwden и нажмите кнопку ОК, чтобы сохранить данные.
Загрузите переменные в рабочую область:
load s_ex4mwden whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
PCA_Params | 1x7 | 2628 | struct array |
x | 1024x4 | 32768 | double array |
Упрощенные сигналы находятся в матрице x. Параметры многомасштабного PCA доступны в PCA_Params:
PCA_Params
PCA_Params =
1x7 struct array with fields:
pc
variances
npc
PCA_Params - массив структуры длины d+2 (здесь максимальный уровень разложения d=5) так, что PCA_Params(d).pc - матрица главных компонентов. Столбцы хранятся в порядке убывания отклонений. PCA_Params(d).variances является вектором отклонений основного компонента, и PCA_Params(d).npc - вектор выбранных чисел сохраненных главных компонентов.