Сеть вейвлет-рассеяния позволяет получать, с минимальной конфигурацией, малодисперсные характеристики из действительных временных рядов и данных изображения для использования в машинном обучении и приложениях глубокого обучения. Элементы нечувствительны к преобразованиям входных данных в определяемой вами шкале инвариантности и являются непрерывными по отношению к деформациям. В 2-D случае элементы также нечувствительны к вращениям. В сети рассеяния используются предопределенные вейвлет-фильтры и фильтры масштабирования.
Маллат вместе с Бруной и Анденом впервые создал математическую основу для изучения сверточных нейронных архитектур [2][3][4][5]. Анден и Лоштанлен разработали эффективные алгоритмы вейвлет-рассеяния 1-D сигналов [4] . [6]Ойаллон разработал эффективные алгоритмы рассеяния 2-D [7]. Andén, Lostanlen и Oyallon являются основными участниками программного обеспечения ScatNet [10] и Kymatio [11] для вычисления преобразований рассеяния.
Маллат и другие охарактеризовали три свойства, которыми обладают архитектуры глубокого обучения для извлечения полезных функций из данных:
Многомасштабные сокращения
Линеаризация иерархических симметрий
Разреженные представления
Сеть вейвлет-рассеяния проявляет все эти свойства. Вейвлет-преобразование линеаризует небольшие деформации, такие как расширения, путем разделения изменений по различным масштабам. Для многих естественных сигналов вейвлет-преобразование также обеспечивает разреженное представление. Комбинируя вейвлет-преобразования с другими признаками сети рассеяния, описанной ниже, преобразование рассеяния создает представления данных, которые минимизируют различия внутри класса, сохраняя при этом различимость между классами. Важное различие между преобразованием рассеяния и сетями глубокого обучения заключается в том, что фильтры определяются априори, а не изучаются. Поскольку преобразование рассеяния не требуется для изучения откликов фильтра, часто можно успешно использовать рассеяние в ситуациях, когда имеется нехватка обучающих данных.
Преобразование вейвлет-рассеяния обрабатывает данные поэтапно. Выход одного каскада становится входным для следующего каскада. Каждый этап состоит из трех операций.

Коэффициенты рассеяния нулевого порядка вычисляются простым усреднением входного сигнала. Вот древовидное представление алгоритма:
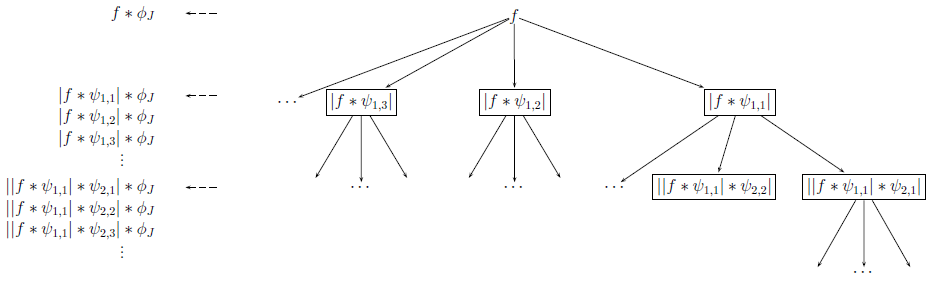
} представляют собой вейвлеты, δ J представляет собой функцию масштабирования, а f представляет собой входные данные. В случае данных изображения, для каждого k, имеется ряд заданных пользователем поворотов вейвлета. Последовательность ребер от корня к узлу называется путем. Узлы дерева являются коэффициентами скалограммы. Коэффициенты рассеяния являются коэффициентами скалограммы, свернутыми с β J). Набор коэффициентов рассеяния представляет собой признаки низкой дисперсии, полученные из данных. Свертка с функцией масштабирования является фильтрацией нижних частот и информация теряется. Однако информация восстанавливается при вычислении коэффициентов на следующей стадии.
Чтобы извлечь элементы из данных, сначала используйте waveletScattering (для временных рядов) или waveletScattering2 (для данных изображения) для создания и настройки сети. Задаваемые параметры включают размер шкалы инвариантности, количество блоков фильтров и количество вейвлетов на октаву в каждом блоке фильтров. В waveletScattering2 можно также задать количество вращений на вейвлет. Для получения элементов из временных рядов используйте waveletScattering функции объекта scatteringTransform или featureMatrix. Для получения элементов из данных изображения используйте waveletScattering2 функции объекта scatteringTransform или featureMatrix.
Преобразование рассеяния генерирует признаки итеративным образом. Сначала сверните данные с функцией масштабирования, для получения S [0] коэффициентов рассеяния нулевого порядка. Далее выполните следующие действия:
Возьмем вейвлет-преобразование входных данных с каждым вейвлет-фильтром в первом наборе фильтров.
Возьмем модуль каждого из отфильтрованных выходов. Узлы являются скалограммой, U [1].
Среднее значение каждого из модулей с помощью фильтра масштабирования. Результаты представляют собой коэффициенты рассеяния первого порядка S [1].
Повторите процесс на каждом узле.
scatteringTransform функция возвращает коэффициенты рассеяния и скалограммы. featureMatrix функция возвращает признаки рассеяния. Оба выходных сигнала могут быть легко использованы алгоритмами обучения, как показано в Vavelet Time Scattering for ECG Signal Classification или Texture Classification Wavelet Image Scattering.
Масштабный фильтр играет решающую роль в сети вейвлет-рассеяния. При создании сети вейвлет-рассеяния задается шкала инвариантности. Сеть инвариантна трансляциям до уровня инвариантности. Поддержка функции масштабирования определяет размер инварианта во времени или пространстве.
Для данных временных рядов шкала инвариантности является длительностью. Временная поддержка функции масштабирования не превышает размера инварианта. На этом графике показана поддержка функции масштабирования в сети со шкалой инвариантности две секунды и частотой дискретизации 100 Гц. Также показаны действительная и мнимая части наиболее масштабного вейвлета из первого набора фильтров. Соблюдайте временные опоры функций не более двух секунд.
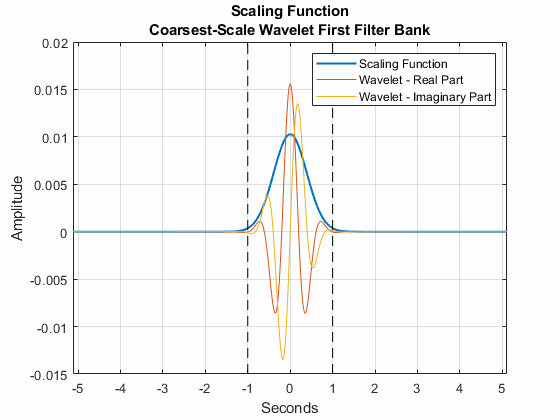
Шкала инвариантности также влияет на расстояния между центральными частотами вейвлетов в блоках фильтров. В банке фильтров, созданном cwtfilterbank, центральные частоты полосы пропускания логарифмически разнесены, и полосы пропускания вейвлетов уменьшаются с центральной частотой.
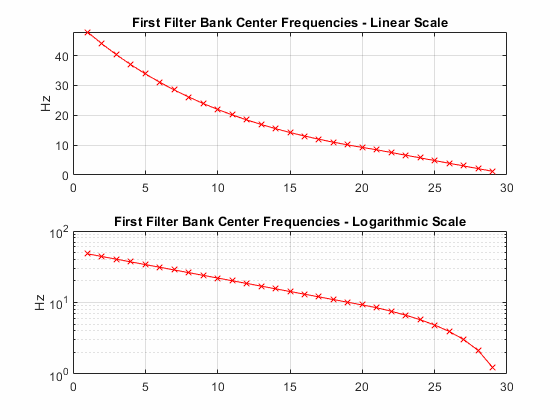
Однако в рассеивающей сети временная поддержка вейвлета не может превышать шкалу инвариантности. Это свойство проиллюстрировано на графике вейвлетов грубого масштаба. Частоты ниже инвариантной шкалы линейно разнесены с постоянной шкалой, так что размер инварианта не превышен. Следующий график показывает центральные частоты вейвлетов в первом наборе фильтров в сети рассеяния. Центральные частоты строятся на линейной и логарифмической шкалах. Обратите внимание на логарифмический интервал между более высокими центральными частотами и линейный интервал между более низкими центральными частотами.
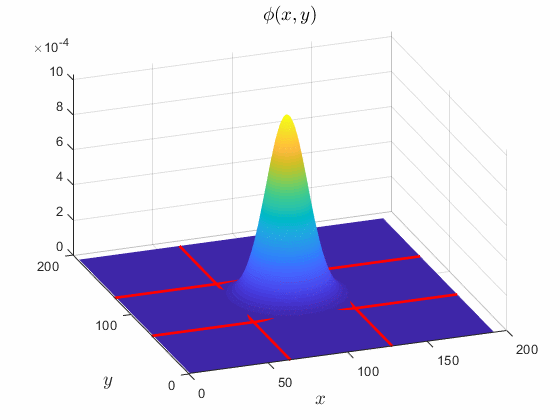
Для данных изображения шкала инвариантности задает пространственную поддержку N-на-N в пикселях фильтра масштабирования. Например, по умолчанию waveletScattering2 функция создает сеть рассеяния вейвлет-изображения для размера изображения 128 на 128 и шкалы инвариантности 64. На следующем графике поверхности показана функция масштабирования, используемая в сети. Пересекающиеся красные линии образуют квадрат 64 на 64.
При создании сети вейвлет-рассеяния в дополнение к шкале инвариантности также задаются коэффициенты качества для банков фильтров рассеяния. Коэффициент качества для каждого набора фильтров - количество вейвлет-фильтров на октаву. Вейвлет-преобразование дискретизирует масштабы, используя заданное количество вейвлет-фильтров.
На этом графике показаны вейвлет-фильтры в сети, созданные waveletScattering. Шкала инвариантности составляет одну секунду, а частота дискретизации - 200 Гц. Первый банк фильтров имеет значение качества по умолчанию 8, а второй банк фильтров имеет коэффициент качества по умолчанию 1.
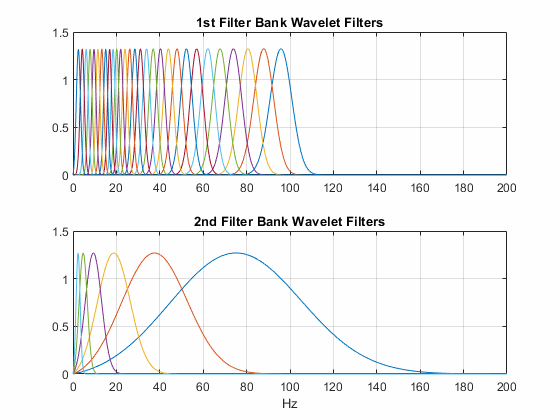
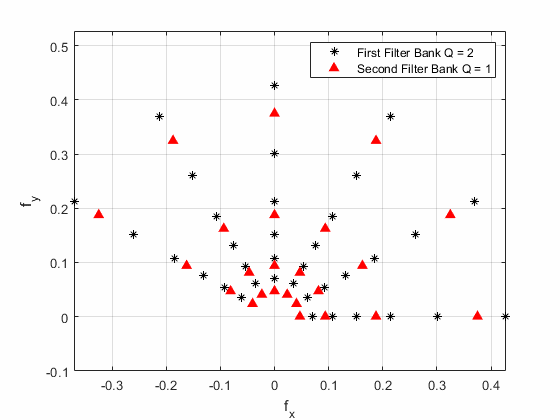
Для данных изображения большие коэффициенты качества не требуются. Большие значения также приводят к значительным вычислительным затратам. По умолчанию waveletScattering2 создает сеть с двумя банками фильтров, каждый из которых имеет коэффициент качества 1. На этом графике показаны центральные частоты вейвлетов для сети рассеяния вейвлет-изображений с двумя блоками фильтров. Первый блок фильтров имеет коэффициент качества 2, а второй блок фильтров имеет коэффициент качества 1. Число вращений на группу фильтров равно 6.
При правильном выборе вейвлетов преобразование рассеяния является неэкспансивным. Энергия рассеивается при итерации по сети. По мере увеличения порядка m энергия коэффициентов скалограммы и коэффициентов рассеяния m-го порядка быстро сходится к 0 [3]. Рассеивание энергии имеет практическую пользу. Можно ограничить количество банков вейвлет-фильтров в сети с минимальной потерей энергии сигнала. Опубликованные результаты показывают, что энергия коэффициентов рассеяния третьего порядка может упасть ниже одного процента. Для большинства приложений достаточно сети с двумя банками вейвлет-фильтров.
Рассмотрим древовидное представление сети вейвлет-временного рассеяния. Предположим, что в первом блоке фильтров имеется M вейвлетов, а во втором блоке фильтров - N вейвлетов. Количество вейвлет-фильтров в каждом наборе фильтров не должно быть большим до того, как наивная реализация станет неосуществимой. Эффективные реализации используют преимущества низкочастотного характера функции модуля и критически понижают коэффициенты рассеяния и скалограммы. Эти стратегии были впервые разработаны Andén, Mallat, Lostanlen и Oyallon [4]
для того, чтобы [6]
сделать [7]преобразования рассеяния вычислительно практичными, сохраняя свою способность создавать представления данных с низкой дисперсией для обучения. По умолчанию waveletScattering и waveletScattering2 создание сетей, которые критически понижают коэффициенты.
[1] ЛеКун, Ю., Б. Босер, Дж. С. Денкер, Д. Хендерсон, Р. Э. Ховард, В. Хаббард и Л. Д. Джакел. «Распознавание рукописных цифр с помощью сети обратного распространения». In Advances in Neural Information Processing Systems (NIPS 1989) (Д. Туретцки, ред.). 396–404. Денвер, CO: Morgan Kaufmann, Vol 2, 1990.
[2] Маллат, С. «Инвариантное рассеяние группы». Коммуникации в чистой и прикладной математике. Том 65, номер 10, 2012, стр. 1331-1398.
[3] Бруна, J. и С. Маллэт. «Инвариантные сети свертки рассеяния». Транзакции IEEE по анализу шаблонов и машинному интеллекту. т. 35, № 8, 2013, с. 1872-1886.
[4] Andén, J. и С. Маллэт. «Спектр глубокого рассеяния». Транзакции IEEE при обработке сигналов. Том 62, номер 16, 2014, стр. 4114-4128.
[5] Маллат, С. «Понимание глубоких сверточных сетей». Философские сделки Королевского общества А. Том 374:20150203, 2016, стр. 1-16. dx.doi.org/10.1098/rsta.2015.0203.
[6] Lostanlen, V. Scattering.m - инструментарий MATLAB для вейвлет-рассеяния. https://github.com/lostanlen/scattering.m.
[7] Ояллон, Эдуар. Веб-страница Эдуара Ойаллона. https://edouardoyallon.github.io/.
[8] Сифре, Л. и С. Маллат. «Рассеяние жесткого движения для классификации текстур». arXiv препринт. 2014, стр 1–19. https://arxiv.org/abs/1403.1687.
[9] Сифре, Л. и С. Маллат. Конференция IEEE 2013 по компьютерному зрению и распознаванию образов. 2013, стр. 1233-1240.
[10] ScatNet. https://www.di.ens.fr/data/software/scatnet/.
[11] Кыматио. https://www.kymat.io/.
waveletScattering | waveletScattering2