Быстрый многополюсный метод для больших структур

Вычислительный метод быстрого мультиполюсного метода (FMM) в Antenna Toolbox™ позволяет моделировать и анализировать антенны и массивы на больших платформах, таких как самолеты и автомобили.

Прямые решатели

Первым шагом в вычислительном решении электромагнитных задач является дискретизация уравнений Максвелла. Процесс приводит к этой матрично-векторной системе:

$V = Z I$

V - Вектор приложенного напряжения. Этот сигнал может быть напряжением или степенью, приложенной к антенне, или падающим сигналом, падающим на антенну.
I - Вектор тока, который представляет ток на поверхности антенны.
Z - Матрица взаимодействия или матрица импеданса, которая относится V к I.

Antenna Toolbox использует Method of Moments Solver для металлических и диэлектрических структур, чтобы вычислить матрицу взаимодействия и решить системные уравнения.

Чтобы вычислить поверхностные токи в структуре антенны, вы сначала задаете базисные функции Рао-Уилтона-Глиссона (RWG). Функция базиса RWG является парой треугольников, которые имеют общее ребро, и показана на рисунке.

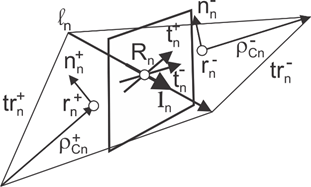
Для любых двух закрашенных фигур треугольника, $t_{n}^{+}$ и $t_{n}^{-}$ , имеющих области $A_{n}^{+}$ и $A_{n}^{-}$ , и совместное использование общего ребра $l_{n}$ , базисная функция

$\begin{array}{l} {\vec{f}}_{n} (\vec{r}) = {\begin{matrix} \frac{l_{n}}{2 A_{n}^{+}} {\vec{ρ}}_{n}^{+ S}, & \vec{r} \in t_{n}^{+} \\ \frac{l_{n}}{2 A_{n}^{-}} {\vec{ρ}}_{n}^{- S}, & \vec{r} \in t_{n}^{-} \end{matrix} \end{array}$

${\vec{ρ}}_{n}^{+} = \vec{r} - {\vec{r}}_{n}^{+}$ - Вектор, нарисованный из свободной вершины треугольника $t_{n}^{+}$ в точку наблюдения $\vec{r}$
${\vec{ρ}}_{n}^{-} = {\vec{r}}_{n}^{+} - \vec{r}$ - Вектор, нарисованный из точки наблюдения, в свободную вершину треугольника $t_{n}^{-}$

$\nabla \cdot {\vec{f}}_{n} (\vec{r}) = {\begin{matrix} \frac{l_{n}}{A_{n}^{+}}, & \vec{r} \in t_{n}^{+} \\ - \frac{l_{n}}{A_{n}^{-}}, & \vec{r} \in t_{n}^{-} \end{matrix}$

Функция базиса является нулем вне двух соседних треугольников $t_{n}^{+}$ и $t_{n}^{-}$ . Вектор базиса RWG линеен и не имеет потока (без нормального компонента) через свой контур.

Отношение между используемой памятью и размером задачи

Матричная Z взаимодействия является комплексной плотной симметричной матрицей. Это квадратная N -by - N матрица, где N - количество базисных функций, то есть количество внутренних ребер в структуре. Рассмотрим сценарий большой конструкции вроде самолета или корабля. Типичные узкополосные антенны, такие как диполь или закрашенная фигура, имеют половину длины волны в размере, но корабли или самолеты часто могут быть по меньшей мере 100 длин волн или более в размере. Чтобы решить для электромагнитных эффектов или излучения, или рассеяния из этой структуры с помощью решателя полной волны, первым шагом является защелкивание структуры и последующее формирование базисных функций. Это создает более 50 000 треугольников. Поскольку требование к памяти для прямого решателя имеет порядок O (N²), в базисе функций, рост как показано на этом графике.

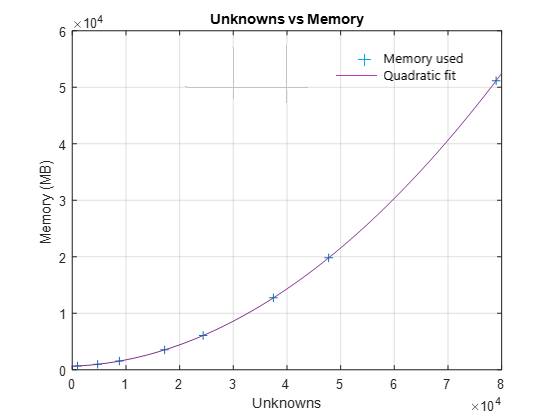
При любом из следующих условий число неизвестных становится очень большим:

Высокая частота анализа
Структура, очищенная более мелким mesh
Анализ физически большой структуры

Быстрый многополюсный метод (FMM)

Ускорение, достигнутое алгоритмом FMM, связано с его способностью подразделять задачу на последовательно меньшие пространственные области, таким образом гарантируя, что взаимодействие между заданной парой исходных и целевых кластеров достаточно отдалено, чтобы оно было вычислено с использованием многополюсных расширений. Следующий рисунок иллюстрирует это.

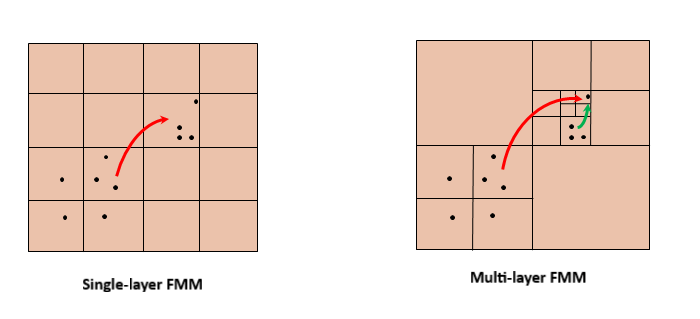
Этот подход хорошо согласуется с нашей необходимостью ускорить расчет взаимодействий между разделенными парами базисных функций, то есть парами исходных и целевых диполов. Задача определения электромагнитного потенциала в заданном наборе целевых точек в типе задачи Гельмгольца может быть выражена:

$u (r) = \sum_{n = 1}^{N} c_{n} \frac{\exp (j k | r - r_{n} |)}{| r - r_{n} |} - v_{n} \cdot \nabla (\frac{\exp (j k | r - r_{n} |)}{| r - r_{n} |})$

где cn _иvn _{представляют}набор степеней заряда и диполя, соответственно, k является числом волн, а u (r) является потенциалом, вычисленным FMM в трехмерном пространстве.

FMM ускоряет расчет матрично-векторного продукта, существенно ускоряя расчет взаимодействий «точка-точка», опосредованных функцией Грина. Исходные распределения тока и заряда на поверхности цели определяются путем введения этих коэффициентов назад в расширение базовой функции. Рассеянное или излучаемое поле цели, включая ее радиолокационные сечения, затем находят путем вычисления излучения известных поверхностных токов и зарядов в необходимых точках пространства. Итерационный подход к определению обратной матрицы является хорошо изученной и устоявшейся областью прикладной линейной алгебры. Среди множества итерационных решателей, которые существуют, обобщенный метод минимального остаточного (GMRES) является хорошо известным методом. Тулбокс Antenna использует этот итерационный решатель.

Интегральное уравнение электрического поля (EFIE)

Прямой решатель, реализованный в Antenna Toolbox, основан на интегральном уравнении электрического поля (EFIE). EFIE использует зависимости электрического поля на поверхности металла и в любой точке свободного пространства, чтобы настроить систему уравнений.

$E_{t}^{s} = - E_{t}^{i}$

$E^{s} (r) = - j ω A - \nabla φ$

Индекс t в первом из двух уравнений используется для описания тангенциального компонента электрического поля на металлической поверхности, индекс s описывает рассеянное поле и индекс i обозначает падающее поле. Во втором уравнении отношение рассеянного поля показано в терминах электрического скалярного потенциала и магнитного векторного потенциала A.

Применение подхода Галеркина, где тест с использованием базисных функций приводит к следующему ключевому уравнению:

$j ω {\frac{l_{m}}{2} p_{m}^{+} (r_{m}^{+}) \cdot A (r_{m}^{+}) + \frac{l_{m}}{2} p_{m}^{-} (r_{m}^{-}) \cdot A (r_{m}^{-})} - {l_{m} φ (r_{m}^{+}) - l_{m} φ (r_{m}^{-})} = V_{m}$

$V_{m} = \frac{l_{m}}{2} p_{m}^{+} (r_{m}^{+}) \cdot E^{i} (r_{m}^{+}) + \frac{l_{m}}{2} p_{m}^{-} (r_{m}^{-}) \cdot E^{i} (r_{m}^{-})$

Интегральное уравнение магнитного поля (MFIE)

Уравнение MFIE выражает поверхностную плотность тока J (r), разработанную на теле металлического объекта в ответ на возбуждение магнитного поля. Важным наблюдением здесь является то, что второй член MFIE является точным приближением физической оптики (PO). Это уравнение захватывает решение первого порядка как приближение ФО, в то время как второй член, включающий интеграл, захватывает эффекты полной волны, таким образом обеспечивая полное решение.

МФИ может применяться только к закрытым конструкциям, таким как коробки, сферы, закрытые интерпретаторы самолета и так далее. Его нельзя применить, например, к полосному диполю или монополярной антенне.

$J (r) = 2 n (r) \times \int_{s} J (r') \times \nabla_{r'} \frac{\exp (- j k | r - r' |)}{4 π | r - r' |} d r' + 2 n (r) \times H^{i} (r)$

Использование подхода коллокации приводит к уравнению для реализации MFIE:

$c_{m} - {I_{m} \cdot \sum_{n = 1}^{N_{f a c e t s}} (\begin{matrix} M_{1} \cdot \nabla \\ M_{2} \cdot \nabla \\ M_{3} \cdot \nabla \end{matrix}) \frac{\exp (- j k | R_{m} - r_{n} |)}{4 π | R_{m} - r_{n} |}} = I_{m}^{P O}$

$M_{1} = (\begin{matrix} 0 \\ - m_{z} \\ + m_{y} \end{matrix}), M_{2} = (\begin{matrix} + m_{z} \\ 0 \\ - m_{x} \end{matrix}), M_{3} = (\begin{matrix} - m_{y} \\ + m_{x} \\ 0 \end{matrix}), m = I_{n} r_{n}$

Объединенное интегральное уравнение поля (CFIE)

CFIE использует два уравнения, показанные для EFIE и MFIE. Термин α выбран, чтобы быть 0.5, и η = 376.3Ω является импедансом свободного пространства.

$α L H S E_{m} + (1 - α) η L H S H_{m} = α V_{m} + (1 - α) η I_{m}^{P O}$

Решатель FMM применяется, чтобы вычислить левую сторону этого уравнения. _LHSEm представляет левую сторону EFIE, а _LHSHm представляет левую сторону MFIE.

Ссылки

[1] Flatironinstitute/FMM3D. Фортран. 2018. Переиздание, Институт Флатирона, 2021. https://github.com/flatironinstitute/FMM3D.

[2] Грингард, Л, и В Рохлин. Быстрый алгоритм симуляций частиц. Журнал вычислительной физики 73, № 2 (декабрь 1987): 325-48. https://doi.org/10.1016/0021-9991 (87) 90140-9.

[3] Rius JM, Übeda E, Parron J. Об проверке интегрального уравнения магнитного поля с базисными функциями RWG в методе моментов. IEEE Trans. Antennas and Propagation, vol. AP-49, no. 11, pp. 1550-1553.

[4] Rao SM, Wilton DR, Glisson AW. Электромагнитное рассеяние поверхностями произвольной формы. Преобразование IEEE на антенны и распространение. 1982 May;30 (3): 409-418. doi: 001 8-926X/82/0500-O409.

Документация