Метод решателя моментов для металлоконструкций

Метод расчета моментов для металлических антенн.

Первым шагом в вычислительном решении электромагнитных задач является дискретизация уравнений Максвелла. Процесс приводит к этой матрично-векторной системе:

$V = Z I$

V - Вектор приложенного напряжения. Этот сигнал может быть напряжением или степенью, приложенной к антенне, или падающим сигналом, падающим на антенну.
I - Вектор тока, который представляет ток на поверхности антенны.
Z - Матрица взаимодействия или матрица импеданса, которая относится V к I.

Antenna Toolbox™ использует метод моментов (MoM), чтобы вычислить матрицу взаимодействия и решить системные уравнения.

Состав MoM

Состав МоМ разделяют на три части.

Дискретизация металлов

Дискретизация позволяет сформулировать формулировку из непрерывной области в дискретную область. Этот шаг называется сеткой в антенной литературе. В МоМ-рецептуре металлическая поверхность антенны зацепляется в треугольники.

Базисные функции

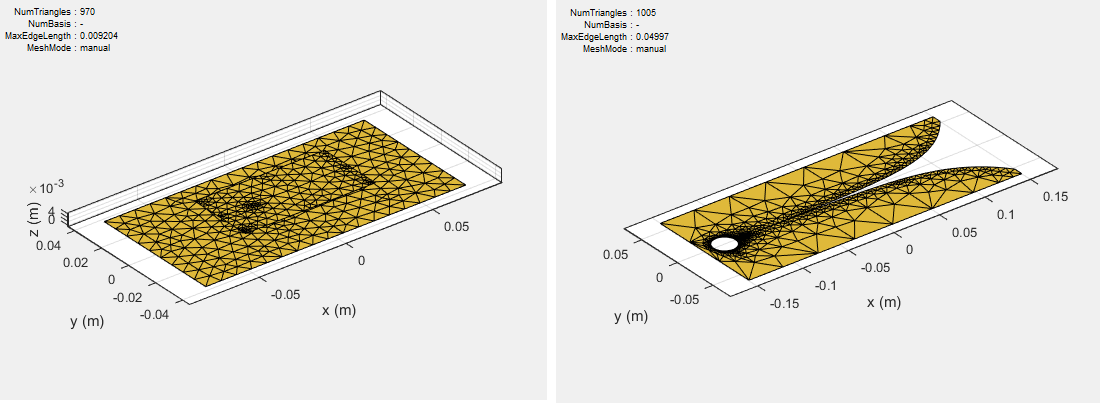
Чтобы вычислить поверхностные токи в структуре антенны, сначала задайте базисные функции. Antenna Toolbox использует базисные функции Рао-Уилтона-Глиссона (RWG) [2]. Стрелы показывают направление потока тока.

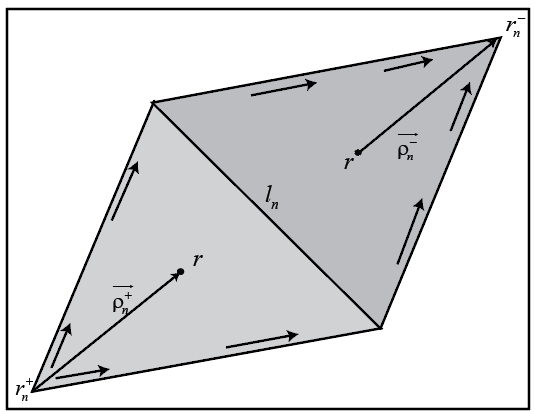
Функция базиса включает пару смежных (не обязательно копланарных) треугольников и напоминает небольшой пространственный диполь с линейным распределением тока. Каждый треугольник связан с положительным или отрицательным зарядом.

Для любых двух закрашенных фигур треугольника, $t_{n}^{+}$ и $t_{n}^{-}$ , имеющих области $A_{n}^{+}$ и $A_{n}^{-}$ , и совместное использование общего ребра $l_{n}$ , базисная функция

$\begin{array}{l} {\vec{f}}_{n} (\vec{r}) = {\begin{matrix} \frac{l_{n}}{2 A_{n}^{+}} {\vec{ρ}}_{n}^{+ S}, & \vec{r} \in t_{n}^{+} \\ \frac{l_{n}}{2 A_{n}^{-}} {\vec{ρ}}_{n}^{- S}, & \vec{r} \in t_{n}^{-} \end{matrix} \end{array}$

${\vec{ρ}}_{n}^{+} = \vec{r} - {\vec{r}}_{n}^{+}$ - Вектор, нарисованный из свободной вершины треугольника $t_{n}^{+}$ в точку наблюдения $\vec{r}$
${\vec{ρ}}_{n}^{-} = {\vec{r}}_{n}^{+} - \vec{r}$ - Вектор, нарисованный из точки наблюдения, в свободную вершину треугольника $t_{n}^{-}$

$\nabla \cdot {\vec{f}}_{n} (\vec{r}) = {\begin{matrix} \frac{l_{n}}{A_{n}^{+}}, & \vec{r} \in t_{n}^{+} \\ - \frac{l_{n}}{A_{n}^{-}}, & \vec{r} \in t_{n}^{-} \end{matrix}$

Функция базиса является нулем вне двух соседних треугольников $t_{n}^{+}$ и $t_{n}^{-}$ . Вектор базиса RWG линеен и не имеет потока (без нормального компонента) через свой контур.

Матрица взаимодействия

Матрица взаимодействия является комплексной плотной симметричной матрицей. Это квадратная N -by - N матрица, где N - количество базисных функций, то есть количество внутренних ребер в структуре. Показана типовая матрица взаимодействия для структуры с 256 базисными функциями:

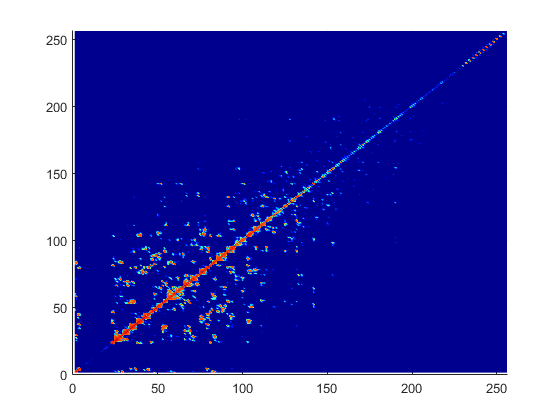
Чтобы заполнить матрицу взаимодействия, вычислите функцию свободного пространства Грина между всеми базисными функциями на поверхности антенны. Конечные матричные уравнения взаимодействия:

$Z_{m n} = (\frac{j ω μ}{4 π}) \int_{S} \int_{S} {\vec{f}}_{m} (\vec{r}) . {\vec{f}}_{m} (\vec{r^{'}}) g d \vec{r^{'}} d \vec{r} - (\frac{j}{4 π ω ε}) \int_{S} \int_{S} (\nabla . {\vec{f}}_{m}) (\nabla . {\vec{f}}_{m}) g d \vec{r^{'}} d \vec{r}$

где

$g (\vec{r}, \vec{r^{'}}) = \frac{\exp (- j k | \vec{r} - \vec{r^{'}} |)}{| \vec{r} - \vec{r^{'}} |}$ - Функция свободного пространства Грина

Чтобы вычислить матрицу взаимодействия, возбудите антенну напряжением 1 В на питающем ребре. Таким образом, вектор напряжения имеет нулевые значения везде, кроме как на ребре. Решите систему уравнений, чтобы вычислить неизвестные токи. После определения неизвестных токов можно вычислить свойства поля и поверхности антенны.

Соседняя область

Из матричного графика взаимодействия вы наблюдаете, что матрица является диагонально доминирующей. Когда вы удаляетесь от диагонали, величина членов уменьшается. Это поведение совпадает с поведением функции Грина. Функция Грина уменьшается, когда расстояние между r и r' увеличений. Поэтому важно точно вычислить область по диагонали и близкую к диагонали.

Эта область на диагонали и вокруг нее называется соседней областью. Соседняя область определяется внутри сферы радиусных R, где R с точки зрения размера треугольника. Размер треугольника - это максимальное расстояние от центра треугольника до любой из его вершин. По умолчанию R вдвое превышает размер треугольника. Для лучшей точности для вычисления интегралов используется схема интегрирования более высокого порядка.

Экстракция особенности

Вдоль диагонали r и r' равны и определяют, что функция Грина становится сингулярной. Чтобы удалить особенность, экстракция выполняется на этих терминах.

$\begin{array}{l} \int_{t_{p}} \int_{t_{q}} ({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j}) g (\vec{r}, \vec{r^{'}}) d s' d s = \int_{t_{p}} \int_{t_{q}} \frac{({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j})}{| \vec{r} - \vec{r^{'}} |} d s' d s + \int_{t_{p}} \int_{t_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1) ({\vec{ρ}}_{i} . {\vec{ρ}}^{'}_{j})}{| \vec{r} - \vec{r^{'}} |} d s' d s \\ \int_{t_{p}} \int_{t_{q}} g (\vec{r}, \vec{r^{'}}) d s' d s = \int_{t_{p}} \int_{t_{q}} \frac{1}{| \vec{r} - \vec{r^{'}} |} d s' d s + \int_{t_{p}} \int_{t_{q}} \frac{(\exp (- j k | \vec{r} - \vec{r^{'}} |) - 1)}{| \vec{r} - \vec{r^{'}} |} d s' d s \end{array}$

Два интеграла в правой части уравнений, называемые потенциальными или статическими интегралами, найдены с помощью аналитических результатов [3].

Конечные массивы

Формулировка MoM для конечных массивов такая же, как и для одного антенного элемента. Основное различие - количество возбуждений (кормов). Для конечных массивов вектор напряжения теперь является матрицей напряжений. Количество столбцов равно количеству элементов в массиве.

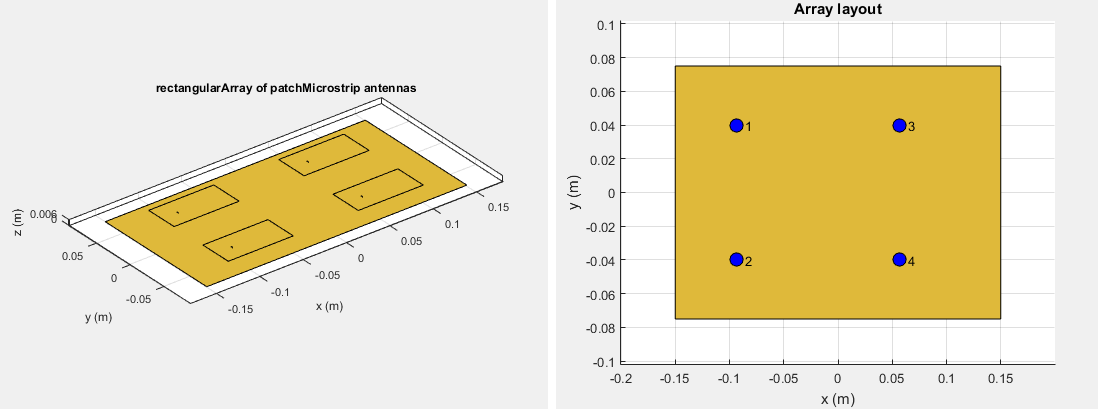
Для примера матрица вектора напряжения для 2x2 массив прямоугольной закрашенная фигура имеет четыре столбца, так как каждая антенна может возбуждаться отдельно.

Бесконечный массив

Чтобы смоделировать бесконечный массив, вы изменяете MoM, чтобы учесть бесконечное поведение. Для этого вы заменяете функции свободного пространства Грина на периодические функции Грина. Периодическая функция Грина является бесконечным двойным суммированием.

Функция Грина	Периодическая функция Грина
$\begin{array}{l} g = \frac{e^{- j k R}}{R} \\ R = \| \vec{r} - {\vec{r}}^{'} \| \end{array}$	$\begin{array}{l} g_{periodic} = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} e^{j ϕ_{m n}} \frac{e^{- j k R_{m n}}}{R_{m n}} \\ R_{m n} = \sqrt{{(x - x^{'} - x_{m})}^{2} + {(y - y^{'} - y_{n})}^{2} + {(z - z^{'})}^{2}} \\ ϕ_{m n} = - k (x_{m} \sin θ \cos φ + y_{n} \sin θ \sin φ) \\ x_{m} = m \cdot d_{x}, y_{n} = n \cdot d_{y} \end{array}$

Функция Грина

Периодическая функция Грина

$\begin{array}{l} g = \frac{e^{- j k R}}{R} \\ R = | \vec{r} - {\vec{r}}^{'} | \end{array}$

$\begin{array}{l} g_{periodic} = \sum_{m = - \infty}^{\infty} \sum_{n = - \infty}^{\infty} e^{j ϕ_{m n}} \frac{e^{- j k R_{m n}}}{R_{m n}} \\ R_{m n} = \sqrt{{(x - x^{'} - x_{m})}^{2} + {(y - y^{'} - y_{n})}^{2} + {(z - z^{'})}^{2}} \\ ϕ_{m n} = - k (x_{m} \sin θ \cos φ + y_{n} \sin θ \sin φ) \\ x_{m} = m \cdot d_{x}, y_{n} = n \cdot d_{y} \end{array}$

d x и _d y являются размерностями наземной плоскости, которые определяют x и y размерности единичной камеры. θ и Φ являются углами скана.

Сравнивая две функции Грина, вы наблюдаете дополнительный экспоненциальный член, который добавляется к бесконечной сумме. Этот _Φmn учитывает сканирование бесконечного массива. Периодическая функция Грина также учитывает эффект взаимного взаимодействия.

Для получения дополнительной информации см. «Бесконечные массивы».

Ссылки

[1] Harringhton, R. F. Расчет by Moment Methods. Нью-Йорк: Макмиллан, 1968.

[2] Рао, С. М., Д. Р. Уилтон и А. У. Глиссон. Электромагнитное рассеяние поверхностями произвольной формы. IEEE. Trans. Antennas and Propagation, Vol. AP-30, № 3, May 1982, pp. 409-418.

[3] Уилтон, Д. Р., С. М. Рао, А. В. Глиссон, Д. Х. Шоберт, О. М. Аль-Бундак. и С. М. Батлер. Потенциальные интегралы для равномерного и линейного распределения источников в полигональных и многогранных областях. IEEE. Транс. антенны и распространение. Том AP-30, № 3, май 1984, с. 276-281.

[4] Balanis, C.A. Antenna Theory. Анализ и проект. 3rd Ed. New York: John Wiley & Sons, 2005.

Документация