Решатель физической оптики

Решатель физической оптики (PO) в Antenna Toolbox™ позволяет вам решить для RCS объекта. В физической оптике падающая подача используется для вычисления токов на поверхности конструкции в ответ на ударную плоскую волну. С доступными токами можно получить рассеянное поле в нужных точках дальнего поля.

Субдоменные базисные функции RWG и дополнительные размерности

Привычные базисный Рао Уилтона Глиссона (RWG) на треугольниках основаны на [2].

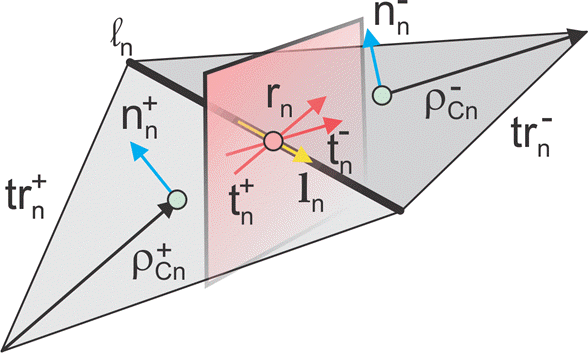
На изображении для двух произвольных треугольных закрашенных фигур _trn⁺ и _trn^- имеющий области _An⁺ и^- и совместное использование общего ребра, _ln базисные функции имеют вид

${\vec{f}}_{n} (\vec{r}) = {\begin{cases} \frac{l_{n}}{2 A_{n}^{+}} {\vec{ρ}}_{n}^{+} \vec{r} в t r_{n}^{+} \\ \frac{l_{n}}{2 A_{n}^{-}} {\vec{ρ}}_{n}^{-} \vec{r} в t r_{n}^{-} \end{cases}} (1)$

где ${\vec{ρ}}_{n}^{+} = \vec{r} - {\vec{r}}_{n}^{-}$ - вектор, нарисованный из свободной вершины треугольника _trn⁺ в точку наблюдения $\vec{r}$ ; ${\vec{ρ}}_{n}^{-} = {\vec{r}}_{n}^{-} - \vec{r}$ - вектор, нарисованный из точки наблюдения в свободную вершину треугольника _trn^-. Функция базиса является нулем вне двух соседних треугольников. Вектор базиса RWG линеен и не имеет потока (то есть не имеет нормального компонента) через свой контур.

От [1], наряду со стандартным определением, этот метод требует двух единичных нормальных векторов ${\vec{n}}_{n}^{\pm}$ и двухмодульные векторы ${\vec{t}}_{n}^{\pm}$ также показан на рисунке. Вектор ${\vec{t}}_{n}^{+}$ - плоскость треугольника _trn⁺; оба вектора перпендикулярны краевым _ln. Они заданы в центре ребра, что _ln обозначается как ${\vec{r}}_{n}$ . Направления ${\vec{t}}_{n}^{\pm}$

также показаны на рисунке. Этот метод принимает, что векторы normal являются правильно (угол между смежными ${\vec{n}}_{n}^{\pm}$ должно быть меньше 180 степени) и однозначно определено. Специфическая векторная ориентация (например, внешние или внутренние нормальные векторы) не имеет значения. Затем мы образуем два вектора перекрестного продукта ${\vec{l}}_{n}^{\pm}$ ,

${\vec{l}}_{n}^{\pm} = {\vec{t}}_{n}^{\pm} \times {\vec{n}}_{n}^{\pm} (2)$

и установить, что оба таких единичных векторов, направленных вдоль ребра, идентичны,

${\vec{l}}_{n}^{\pm} = {\vec{l}}_{n}^{-} = {\vec{l}}_{n} (3)$

Только вектор ${\vec{l}}_{n}$ в конечном счете это необходимо.

Поиск _IPO

Подходящее приближение ФО имеет форму:

$\vec{J} (\vec{r}) = 2 δ (\vec{r}) [\vec{n} (\vec{r}) \times \vec{H} (\vec{r})] (5)$

где и учитывает эффекты затенения. Если наблюдательный пост находится в затененной области, δ должен быть нулем. В противном случае это равняется ± 1 в зависимости от направления падения относительно ориентации вектора normal $\vec{n} (\vec{r})$ . Использование Eq. (4) дает:

$\sum_{n = 1}^{N_{P O}} I_{n}^{P O} {\vec{f}}_{n} (\vec{r}) = 2 δ (\vec{r}) [\vec{n} (\vec{r}) \times \vec{H} (\vec{r})] (6)$

Ref [3] описывает элегантный способ выражения неизвестных $I_{n}^{P O}$ явно, с использованием интересного изменения метода коллокации. Сначала рассмотрим точку сползания, которая стремится к центру ребра ${\vec{r}}_{n}$ функции центрального базиса ${\vec{f}}_{n} (\vec{r})$ и расположен в плюс треугольнике. Умножьте Eq. (6) на вектор ${\vec{t}}_{n}^{+}$ . Поскольку нормальный компонент функции базиса на ребре является одним, а все другие функции базиса, имеющие тот же треугольник, не имеют нормального компонента на ребре, результат становится

$I_{n}^{P O} = 2 δ ({\vec{r}}_{n}) {\vec{t}}_{n}^{+} \cdot [{\vec{n}}_{n}^{+} \times \vec{H} ({\vec{r}}_{n})] (7 a)$

Повторите ту же операцию с минусовым треугольником:

$I_{n}^{P O} = 2 δ ({\vec{r}}_{n}) {\vec{t}}_{n}^{-} \cdot [{\vec{n}}_{n}^{-} \times \vec{H} ({\vec{r}}_{n})] (7 b)$

Добавьте уравнения 7 (a) и 7 (b), разделите результат на два и преобразуйте тройной векторный продукт, чтобы получить:

$I_{n}^{P O} = \frac{2 δ ({\vec{r}}_{n}) \vec{H} ({\vec{r}}_{n}) \cdot ([{\vec{t}}_{n}^{+} \times {\vec{n}}_{n}^{+}] + [{\vec{t}}_{n}^{-} \times {\vec{n}}_{n}^{-}])}{2} (8)$

Поэтому, согласно уравнениям (2) и (3),

$I_{n}^{P O} = 2 δ ({\vec{r}}_{n}) \vec{H} ({\vec{r}}_{n}) \cdot {\vec{l}}_{n} (9)$

Определение освещенных или теневых областей

Вычисление $δ (\bar{r})$ должен учитывать эффект затенения. Для простых выпуклых структур использование нормали для проверки направления излучения будет указывать на освещенную или теневую область. Если нормаль треугольника указывает в противоположном направлении излучения, то грань освещается. Если нормаль треугольника находится в том же направлении, то грань затенена. Но этот простой тест терпит неудачу, когда объект является неконвексным, как в случае с более сложными структурами. Чтобы обработать это, выполните тест пересечения сегмент-треугольник, чтобы строго определить значение $δ (\bar{r})$ . Значение $δ (\bar{r})$ 0 для теневых граней или ± 1 в зависимости от направления падения относительно ориентации вектора normal. Чтобы реализовать это относительно функций базиса RWG, которые формируются на поверхности области ФО, проверяйте на оба произвольных треугольных патча $t r_{n}^{+}$ и $t r_{n}^{-}$ находиться в освещенной области и только затем учитывать вклад, вносимый ребром в вычисление тока ПО. Если любой из треугольников находится в теневой области, значение дельты вычисляется равным нулю, и поэтому ребро не способствует.

Ссылки

[1] U. Jakobus and F. M. Landstorfer, «Улучшенная формулировка PO-MM для рассеяния от трехмерных идеально проводящих тел произвольной формы», IEEE Trans. антенны и распространение, vol. AP-43, no. 2, p.

[2] С. М. Рао, Д. Р. Уилтон, и А. У. Глиссон, «Электромагнитное рассеяние поверхностями произвольной формы», IEEE Trans. Antennas and Propagation, vol. AP-30, no. 3, pp. 409-418, May 1982.

[3] S. Makarov, Antenna and EM Modeling in MATLAB, Wiley, New York, 2002.

Документация