Решатель проводов

wire solver

Ниже приведено сокращенное описание вывода уравнений, решенных решателем проводов. Для получения дополнительной информации см. раздел [1].

Для проводов PEC (Perfect электрически проводящих), граничные условия требуют, чтобы тангенциальный компонент общего электрического поля на поверхности провода был нулем:

${(E + E_{i})}_{\tan} = 0 (1)$

Можно также выразить уравнение в терминах плотности поверхностного тока, ${\vec{J}}_{s}$ , на проводе PEC и его пространственной производной. Это делается путем интегрирования эффекта поверхностной плотности тока с помощью функции Грина, $g (| \vec{r} - {\vec{r}}^{'} |)$ . Функция Грина абстрактно представляет эффект бесконечного источника плотности поверхностного тока, расположенного в ${\vec{r}}^{'}$ на электрическом и магнитном полях в точке наблюдения $\vec{r}$ . Функция Грина для распространения свободного пространства:

$g (| \vec{r} - {\vec{r}}^{'} |) = \frac{\exp (- j k | \vec{r} - {\vec{r}}^{'} |)}{4 π | \vec{r} - {\vec{r}}^{'} |} (2)$

где $k = ω \sqrt{ε_{0} μ_{0}}$ - число волн, а,, - угловая частота. В целом, следующие шаги необходимы, чтобы решить электромагнитную задачу (EM) и получить поля EM в среде. Чтобы точно представлять задачу ЭМ, как продольные, так и поперечные компоненты интегрированного тока берутся в фактор на поверхности провода и требуют, чтобы Эк. (1) удерживал всю поверхность провода. Дискретизируйте Eq. (1) по конечному набору точек или базисных функций, чтобы получить набор уравнений. Дискретизируйте поверхностную плотность тока в конечный набор базисных функций, чтобы получить набор неизвестных. Решите набор уравнений неизвестных, чтобы получить дискретное приближение к поверхностным токам-плотностям на проводе. Эти плотности тока позволяют вычислять электромагнитные поля в любой желаемой точке. Для тонких проводов вышеописанные шаги являются исчерпывающими и упрощают функцию Грина до:

$g (r_{a}) = \frac{\exp (- j k r_{a})}{4 π r_{a}} (3)$

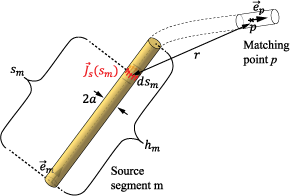
также упоминается как тонкопроводное приближение ядра, где $r_{a} = \sqrt{r^{2} + a^{2}}$ является приблизительным средним значением расстояния $| \vec{r} - {\vec{r}}^{'} |$ r - расстояние между источником плотности тока бесконечной поверхности и осью провода, и a - радиус провода. В сложение плотность тока на проводе заменяется током провода $I = 2 π a | {\vec{J}}_{s} |$ |. Используя вышеописанное приближение, запишите Eq. (1) как:

${(- j ω μ_{0} \int_{s} [(I s) \vec{e} (s) g (r_{a}) + \frac{1}{k^{2}} \frac{d I (s)}{d s} \vec{\nabla} g (r_{a})] d s + {\vec{E}}_{i})}_{\tan} = 0 (4)$

где s - продольное положение вдоль провода и $\vec{e} (s)$ - вектор модуля, представляющий ориентацию провода в этом месте. Дискретизируйте провод в конечное число сегментов s(m) где m = 1....Nи затем дополнительно дискретизируйте Eq. (4) в конечный набор уравнений, накладываемых в точках, совпадающих p = 1....N для получения:

$\sum_{m = 1}^{N} \int_{0}^{h_{m}} [{\vec{e}}_{p} {\vec{e}}_{m} I_{m} (s_{m}) + \frac{{\vec{e}}_{p}}{k^{2}} \frac{d I_{m} (s_{m})}{d s_{m}} \nabla] g (r_{a}) d s_{m} = \frac{{\vec{e}}_{p} {\vec{E}}_{i}}{j ω μ_{0}} (5)$

где _Im(sm) - распределение тока вдоль сегмента m аппроксимированное полиномом вида:

$I_{m} (s_{m}) = {\sum_{i = 0}^{n_{m}} I_{m, i} (\frac{s_{m} - \frac{h_{m}}{2}}{h_{m}})}^{i}, 0 \leq s_{m} \leq h_{m}, m = 1, ...., N (6)$

с _hm длина сегмента и _nm выбранной степенью полинома (который отличается от сегмента к сегменту). Подставляя Eq. (6) в (5), набор уравнений может быть записан в матричном формате как:

$[Z_{p, m i}] [I_{m i}] = [V_{e x, p}] (7)$

где [_Zp,mi] - импедансная матрица, [_Imi] - вектор неизвестных коэффициентов, представляющих ток на проводе, и [_Vexp,p] - вектор возбуждения. Подробнее об вычислении элементов [_Zp,mi] см. в [1].

Ссылки

[1] Попович, Б.К., М. Б. Драгович и А. Р. Джорджевич. Анализ и синтез исследований проводных антенн Press, 1982

Документация по Antenna Toolbox

Поддержка

Памятка переводчика

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.