Эквализация

Эквализация (EQ) является процессом взвешивания частотного спектра аудиосигнала.

Вы можете использовать эквализацию для:

Улучшайте аудиозаписи
Анализ спектрального содержимого

Типы эквализации включают:

Lowpass и highpass фильтры -- Ослабить высокую частоту и низкочастотное содержание, соответственно.
Низкополочные и высокополочные эквалайзеры - повышают или режут частоты одинаково выше или ниже желаемой точки отсечения.
Параметрические эквалайзеры -- Селективно увеличивайте или сокращайте полосы частот. Также известен как пиковые фильтры.
Графические эквалайзеры - избирательно повышайте или вырезайте октавные или дробные октавные полосы частот. Полосы имеют основанные на стандартах центральные частоты. Графические эквалайзеры являются частным случаем параметрических эквалайзеров.

В этом руководстве описывается, как Audio Toolbox™ реализует функции проекта: designParamEQ, designShelvingEQ, и designVarSlopeFilter. The multibandParametricEQ Система object™ объединяет функции создания фильтра в многополосный параметрический эквалайзер. The graphicEQ Системный объект объединяет функции создания фильтра и octaveFilter Системный объект для основанного на стандартах графической эквализации. Для руководства, посвященного использованию функций проекта в MATLAB^®, см. Parametric Equalizer Design.

Уравнение Проекта использованием Audio Toolbox

Тип эквалайзера и расчётные параметры Примеры реакции величины

Тип эквалайзера и расчётные параметры	Примеры реакции величины
Использовать `designVarSlopeFilter` для создания lowpass и highpass фильтров. Расчётные параметры `designVarSlopeFilter` включают: Нормированная частота среза Наклон (дБ/октава)	Lowpass	Highpass
Использовать `designShelvingEQ` для создания низкополочных и высокополочных эквалайзеров Расчётные параметры `designShelvingEQ` включают: Коэффициент усиления (дБ) Нормированная частота среза Наклон (дБ/октава)	Низкополочный	Высокая Полка
Использовать `designParamEQ` для создания параметрических эквалайзеров. Можно проектировать однополосные параметрические эквалайзеры или каскад параметрических эквалайзеров. Использование каскада параметрических эквалайзеров позволяет вам настроить частотную характеристику с точностью. Расчётные параметры `designParamEQ` включают: Количество полос эквалайзера Коэффициент усиления (дБ) Нормированная шумовая полоса Нормированная центральная частота Порядок фильтрации	Параметрический эквалайзер	Каскад параметрических эквалайзеров

Использовать designVarSlopeFilter для создания lowpass и highpass фильтров.

Расчётные параметры designVarSlopeFilter включают:

Нормированная частота среза
Наклон (дБ/октава)

Lowpass

Highpass

Использовать designShelvingEQ для создания низкополочных и высокополочных эквалайзеров

Расчётные параметры designShelvingEQ включают:

Коэффициент усиления (дБ)
Нормированная частота среза
Наклон (дБ/октава)

Низкополочный

Высокая Полка

Использовать designParamEQ для создания параметрических эквалайзеров. Можно проектировать однополосные параметрические эквалайзеры или каскад параметрических эквалайзеров. Использование каскада параметрических эквалайзеров позволяет вам настроить частотную характеристику с точностью.

Расчётные параметры designParamEQ включают:

Количество полос эквалайзера
Коэффициент усиления (дБ)
Нормированная шумовая полоса
Нормированная центральная частота
Порядок фильтрации

Параметрический эквалайзер

Каскад параметрических эквалайзеров

Создание фильтра

Функции разработки Audio Toolbox используют метод билинейного преобразования создания цифровых фильтров, чтобы определить коэффициенты эквалайзера. В методе билинейного преобразования вы:

Выберите аналоговый прототип.
Задайте параметры создания фильтра.
Выполните билинейное преобразование.

Аналоговый прототип нижней полки

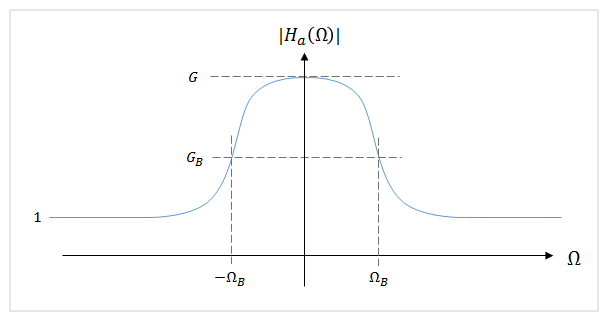
Audio Toolbox использует проект параметрического эквалайзера высокого порядка, представленную в [1]. В этом методе проекта аналоговый прототип принимается как низкополочный фильтр Баттерворта:

$H_{a} (s) = {[\frac{g β + s}{β + s}]}^{r} \prod_{i = 1}^{L} [\frac{g^{2} β^{2} + 2 g s_{i} β s + s^{2}}{β^{2} + 2 s_{i} β s + s^{2}}]$

$• L$ = Количество аналоговых секций SOS

$• N$ = Порядок аналогового фильтра

$• r = {\begin{matrix} 0 N даже \\ 1 N странный \end{matrix}$

$• g = G^{1 / N}$

$• β = Ω_{B} \times {(\sqrt{\frac{G^{2} - G_{B}^{2}}{G_{B}^{2} - 1}})}^{- \frac{1}{N}} = \tan (π \frac{Δ ω}{2}) \times {(\sqrt{\frac{G^{2} - G_{B}^{2}}{G_{B}^{2} - 1}})}^{- \frac{1}{N}}$ , где Δω - необходимая цифровая полоса пропускания

$• s_{i} = \sin (\frac{(2 i - 1) π}{2 N}), i = 1, 2, ..., L$

Для параметрических эквалайзеров аналоговый прототип уменьшается путем установки коэффициента усиления полосы в квадратный корень пикового усиления (G B = sqrt(G)).

После того, как расчётные параметры заданы, аналоговый прототип преобразуется непосредственно в нужный цифровой эквалайзер полосно-пропускающим билинейным преобразованием:

$s = \frac{1 - 2 \cos (ω_{0}) z^{- 1} + z^{- 2}}{1 - z^{- 2}}$

_ω0 цифровая центральная частота.

Это преобразование удваивает порядок фильтра. Каждая аналоговая секция первого порядка становится цифровой секцией второго порядка. Каждая аналоговая секция второго порядка становится цифровой секцией четвертого порядка. Audio Toolbox всегда вычисляет цифровые разделы четвертого порядка, что означает, что возврат секций второго порядка требует расчета корней и менее эффективен.

Цифровые коэффициенты

Цифровая передаточная функция реализована как каскад секций второго и четвертого порядка.

$H (z) = {[\frac{b_{00} + b_{01} z^{- 1} + b_{02} z^{- 2}}{1 + a_{01} z^{- 1} + a_{02} z^{- 2}}]}^{r} \prod_{i = 1}^{L} [\frac{b_{i 0} + b_{i 1} z^{- 1} + b_{i 2} z^{- 2} + b_{i 3} z^{- 3} + b_{i 4} z^{- 4}}{1 + a_{i 1} z^{- 1} + a_{i 2} z^{- 2} + a_{i 3} z^{- 3} + a_{i 4} z^{- 4}}]$

Коэффициенты заданы путем выполнения билинейного преобразования полосы пропускания на проекте аналогового прототипа.

Коэффициенты секции второго порядка	Коэффициенты разделов четвертого порядка
$\begin{array}{l} D_{0} = β + 1 \\ b_{00} = (1 + g β) / D_{0} \\ b_{01} = - 2 \cos (ω_{0}) / D_{0} \\ b_{02} = (1 - g β) / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0} \\ a_{02} = (1 - β) / D_{0} \end{array}$	$\begin{array}{l} D_{i} = β^{2} + 2 s_{i} β + 1 \\ b_{i 0} = (g^{2} β^{2} + 2 g s_{i} β + 1) / D_{i} \\ b_{i 1} = - 4 c_{0} (1 + g s_{i} β) / D_{i} \\ b_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - g^{2} β^{2}) / D_{i} \\ b_{i 3} = - 4 c_{0} (1 - g s_{i} β) / D_{i} \\ b_{i 4} = (g^{2} β^{2} - 2 g s_{i} β + 1) / D_{i} \\ a_{i 1} = - 4 c_{0} (1 + s_{i} β) / D_{i} \\ a_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - β^{2}) / D_{i} \\ a_{i 3} = - 4 \cos (ω_{0}) (1 - s_{i} β) / D_{i} \\ a_{i 4} = (β^{2} - 2 s_{i} β + 1) / D_{i} \end{array}$

Коэффициенты секции второго порядка

Коэффициенты разделов четвертого порядка

$\begin{array}{l} D_{0} = β + 1 \\ b_{00} = (1 + g β) / D_{0} \\ b_{01} = - 2 \cos (ω_{0}) / D_{0} \\ b_{02} = (1 - g β) / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0} \\ a_{02} = (1 - β) / D_{0} \end{array}$

$\begin{array}{l} D_{i} = β^{2} + 2 s_{i} β + 1 \\ b_{i 0} = (g^{2} β^{2} + 2 g s_{i} β + 1) / D_{i} \\ b_{i 1} = - 4 c_{0} (1 + g s_{i} β) / D_{i} \\ b_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - g^{2} β^{2}) / D_{i} \\ b_{i 3} = - 4 c_{0} (1 - g s_{i} β) / D_{i} \\ b_{i 4} = (g^{2} β^{2} - 2 g s_{i} β + 1) / D_{i} \\ a_{i 1} = - 4 c_{0} (1 + s_{i} β) / D_{i} \\ a_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - β^{2}) / D_{i} \\ a_{i 3} = - 4 \cos (ω_{0}) (1 - s_{i} β) / D_{i} \\ a_{i 4} = (β^{2} - 2 s_{i} β + 1) / D_{i} \end{array}$

Биквадратичный случай. В биквадратическом случае, когда N = 1, коэффициенты уменьшаются до:

$\begin{array}{l} D_{0} = \frac{Ω_{B}}{\sqrt{G}} + 1 \\ b_{00} = (1 + Ω_{B} \sqrt{G}) / D_{0}, b_{01} = - 2 \cos (ω_{0}) / D_{0}, b_{02} = (1 - Ω_{B} \sqrt{G}) / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0}, a_{02} = (1 - \frac{Ω_{B}}{\sqrt{G}}) / D_{0} \end{array}$

Денормализация коэффициента a ₀₀ и замена A = sqrt(G) , $Ω_{B} ≅ α$ приводит к знакомым пиковым коэффициентам EQ, описанным в [2].

Орфанидис отмечает приблизительную эквивалентность Ω B и $α$ в [1].

При помощи тригонометрических тождеств,

$Ω_{B} = \tan (\frac{Δ ω}{2}) = \sin (ω_{0}) \sinh (\frac{\ln 2}{2} B),$

где B играет роль эквивалентной октавной полосы пропускания.

Бристоу-Джонсон получил приблизительное решение для B в [4]:

$B = \frac{ω_{0}}{\sin ω_{0}} \times B W$

Подстановка приближения для B в Ω B уравнение приводит к определению $α$ в [2]:

$α = \sin (ω_{0}) \sinh (\frac{\ln 2}{2} \times \frac{ω_{0}}{\sin ω_{0}} \times B W)$

Lowpass и Highpass Создания фильтра

Аналоговый прототип нижней полки

Для разработки lowpass и highpass фильтров Audio Toolbox использует специальный случай создания фильтра для параметрических эквалайзеров. В этом проекте пиковое усиление, G, устанавливается на 0, и G B² установлено на 0,5 (срез -3 дБ). Частота отключения lowpass соответствует 1 - Ω B. Частота отключения высокоскоростного фильтра соответствует _ΩB.

Цифровые коэффициенты

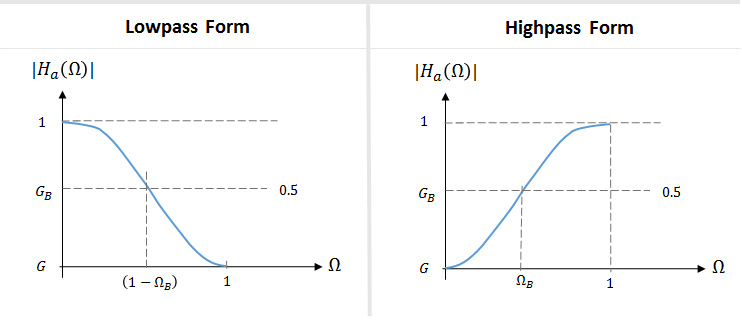
Таблица суммирует результаты билинейного преобразования полосы пропускания. Цифровая центральная частота, ω 0, установлена в π для lowpass фильтров и 0 для высокочастотных фильтров.

Коэффициенты секции второго порядка	Коэффициенты секции четвертого порядка
$\begin{array}{l} D_{0} = 1 + \tan (π \frac{Δ ω}{2}) \\ b_{00} = 1 / D_{0} \\ b_{01} = - 2 \cos (ω_{0}) / D_{0} \\ b_{02} = 1 / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0} \\ a_{02} = (1 - \tan (π \frac{Δ ω}{2})) / D_{0} \end{array}$	$\begin{array}{l} D_{i} = \tan^{2} (π \frac{Δ ω}{2}) + 2 s_{i} \tan (π \frac{Δ ω}{2}) + 1 \\ b_{i 0} = 1 / D_{i} \\ b_{i 1} = - 4 \cos (ω_{0}) / D_{i} \\ b_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0})) / D_{i} \\ b_{i 3} = - 4 \cos {(ω_{0})}_{0} / D_{i} \\ b_{i 4} = 1 / D_{i} \\ a_{i 1} = - 4 \cos (ω_{0}) (1 + s_{i} \tan (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - \tan^{2} (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 3} = - 4 \cos (ω_{0}) (1 - s_{i} \tan (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 4} = (\tan^{2} (π \frac{Δ ω}{2}) - 2 s_{i} \tan (π \frac{Δ ω}{2}) + 1) / D_{i} \end{array}$

Коэффициенты секции второго порядка

Коэффициенты секции четвертого порядка

$\begin{array}{l} D_{0} = 1 + \tan (π \frac{Δ ω}{2}) \\ b_{00} = 1 / D_{0} \\ b_{01} = - 2 \cos (ω_{0}) / D_{0} \\ b_{02} = 1 / D_{0} \\ a_{01} = - 2 \cos (ω_{0}) / D_{0} \\ a_{02} = (1 - \tan (π \frac{Δ ω}{2})) / D_{0} \end{array}$

$\begin{array}{l} D_{i} = \tan^{2} (π \frac{Δ ω}{2}) + 2 s_{i} \tan (π \frac{Δ ω}{2}) + 1 \\ b_{i 0} = 1 / D_{i} \\ b_{i 1} = - 4 \cos (ω_{0}) / D_{i} \\ b_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0})) / D_{i} \\ b_{i 3} = - 4 \cos {(ω_{0})}_{0} / D_{i} \\ b_{i 4} = 1 / D_{i} \\ a_{i 1} = - 4 \cos (ω_{0}) (1 + s_{i} \tan (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 2} = 2 (1 + 2 \cos^{2} (ω_{0}) - \tan^{2} (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 3} = - 4 \cos (ω_{0}) (1 - s_{i} \tan (π \frac{Δ ω}{2})) / D_{i} \\ a_{i 4} = (\tan^{2} (π \frac{Δ ω}{2}) - 2 s_{i} \tan (π \frac{Δ ω}{2}) + 1) / D_{i} \end{array}$

Создание фильтра

Аналоговый прототип

Audio Toolbox реализует создание фильтра, представленный в [2]. В этом проекте аналоговые прототипы с высокой и низкой полками представлены отдельно:

$H_{L} (s) = A (\frac{A s^{2} + (\frac{\sqrt{A}}{Q}) s + 1}{s^{2} + (\frac{\sqrt{A}}{Q}) s + A}) H_{H} (s) = A (\frac{s^{2} + (\frac{\sqrt{A}}{Q}) s + A}{A s^{2} + (\frac{\sqrt{A}}{Q}) s + 1})$

Для компактности аналоговые фильтры представлены с переменными A и Q. Можно преобразовать A и Q в доступные параметры Audio Toolbox design:

$\begin{array}{l} A = 10^{G / 40} \\ \frac{1}{Q} = \sqrt{(A + \frac{1}{A}) (\frac{1}{s l o p e} - 1) + 2} \end{array}$

После того, как вы задаете расчётные параметры, аналоговый прототип преобразуется в желаемый цифровой стеллажный фильтр билинейным преобразованием с предваркой:

$s = (\frac{z - 1}{z + 1}) \times (\frac{1}{\tan (\frac{ω_{0}}{2})})$

Цифровые коэффициенты

Таблица суммирует результаты билинейного преобразования с предваркой.

Низкополочный	Высокая Полка	Промежуточные переменные
$\begin{array}{l} b_{0} = A ((A + 1) - (A - 1) \cos (ω_{0}) + 2 α \sqrt{A}) \\ b_{1} = 2 A ((A - 1) - (A + 1) \cos (ω_{0})) \\ b_{2} = A ((A + 1) - (A - 1) \cos (ω_{0}) - 2 α \sqrt{A}) \\ a_{0} = (A + 1) + (A - 1) \cos (ω_{0}) + 2 α \sqrt{A} \\ a_{1} = - 2 ((A - 1) + (A + 1) \cos (ω_{0})) \\ a_{2} = (A + 1) + (A - 1) \cos (ω_{0}) - 2 α \sqrt{A} \end{array}$	$\begin{array}{l} b_{0} = A ((A + 1) + (A - 1) \cos (ω_{0}) + 2 α \sqrt{A}) \\ b_{1} = - 2 A ((A - 1) + (A + 1) \cos (ω_{0})) \\ b_{2} = A ((A + 1) + (A - 1) \cos (ω_{0}) - 2 α \sqrt{A}) \\ a_{0} = (A + 1) - (A - 1) \cos (ω_{0}) + 2 α \sqrt{A} \\ a_{1} = 2 ((A - 1) + (A + 1) \cos (ω_{0})) \\ a_{2} = (A + 1) - (A - 1) \cos (ω_{0}) - 2 α \sqrt{A} \end{array}$	$\begin{array}{l} α = \frac{\sin (ω_{0})}{2} \sqrt{(A + \frac{1}{A}) (\frac{1}{s l o p e} - 1) + 2 A} \\ ω_{0} = 2 π \frac{C u t o f f F r e q u e n c y}{F s} \end{array}$

Низкополочный

Высокая Полка

Промежуточные переменные

$\begin{array}{l} b_{0} = A ((A + 1) - (A - 1) \cos (ω_{0}) + 2 α \sqrt{A}) \\ b_{1} = 2 A ((A - 1) - (A + 1) \cos (ω_{0})) \\ b_{2} = A ((A + 1) - (A - 1) \cos (ω_{0}) - 2 α \sqrt{A}) \\ a_{0} = (A + 1) + (A - 1) \cos (ω_{0}) + 2 α \sqrt{A} \\ a_{1} = - 2 ((A - 1) + (A + 1) \cos (ω_{0})) \\ a_{2} = (A + 1) + (A - 1) \cos (ω_{0}) - 2 α \sqrt{A} \end{array}$

$\begin{array}{l} b_{0} = A ((A + 1) + (A - 1) \cos (ω_{0}) + 2 α \sqrt{A}) \\ b_{1} = - 2 A ((A - 1) + (A + 1) \cos (ω_{0})) \\ b_{2} = A ((A + 1) + (A - 1) \cos (ω_{0}) - 2 α \sqrt{A}) \\ a_{0} = (A + 1) - (A - 1) \cos (ω_{0}) + 2 α \sqrt{A} \\ a_{1} = 2 ((A - 1) + (A + 1) \cos (ω_{0})) \\ a_{2} = (A + 1) - (A - 1) \cos (ω_{0}) - 2 α \sqrt{A} \end{array}$

$\begin{array}{l} α = \frac{\sin (ω_{0})}{2} \sqrt{(A + \frac{1}{A}) (\frac{1}{s l o p e} - 1) + 2 A} \\ ω_{0} = 2 π \frac{C u t o f f F r e q u e n c y}{F s} \end{array}$

Ссылки

[1] Orfanidis, Sophocles J. «High-Order Digital Parametric Equalizer Design». Журнал Общества аудиотехники. Том 53, ноябрь 2005, стр. 1026-1046.

[2] Бристоу-Джонсон, Роберт. «Формулы Cookbook для коэффициентов биквадного фильтра Audio EQ». Доступ получен 02 марта 2016 года. http://www.musicdsp.org/files/Audio-EQ-Cookbook.txt.

[3] Orfanidis, Sophocles J. Введение в обработку сигналов. Englewood Cliffs, Нью-Джерси: Prentice Hall, 2010.

[4] Бристоу-Джонсон, Роберт. Эквивалентность различных методов вычисления биквадных коэффициентов для аудиопараметрических эквалайзеров. Представлено на 97-й Конвенции AES, Сан-Франциско, ноябрь 1994 года, AES Preprint 3906.

См. также

designParamEQ | designShelvingEQ | designVarSlopeFilter | graphicEQ | multibandParametricEQ

Документация