Flux-Based PM Controller

Контроллер для синхронного двигателя с постоянными магнитами на основе потока

Библиотека:
Блок-набор силовых агрегатов/Двигатель/Регуляторы электродвигателя

Описание

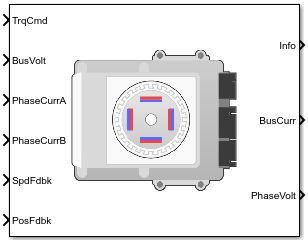
Блок Flux Based PM Controller реализует векторный векторный контроллер для внутреннего синхронного двигателя с постоянными магнитами (PMSM) с опциональным контроллером внешнего контура скорости. Внутреннее управление крутящим моментом реализует стратегии достижения максимального крутящего момента на ампер (MTPA) и ослабления магнитного потока. Можно задать тип управления скоростью или крутящим моментом.

Этот Flux Based PM Controller реализует уравнения для регулирования скорости, определения крутящего момента, регуляторов, преобразований и двигателей.

Рисунок иллюстрирует информационный поток в блоке.

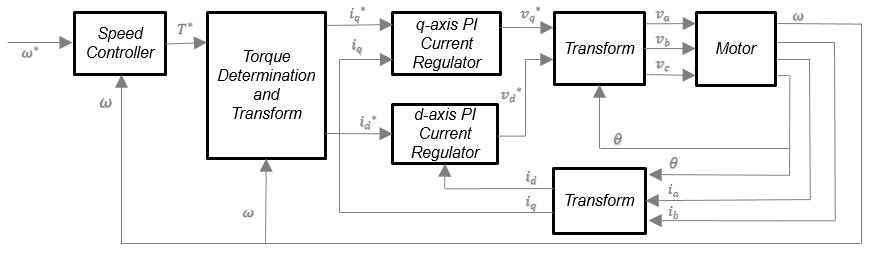
Блок реализует уравнения, используя эти переменные.

ω	Скорость ротора
ω*	Команда скорости ротора
T*	Команда крутящего момента
_id _id*	d-составляющая тока d-составляющая тока команды
_iq _iq*	q-составляющая тока q-составляющая тока команды
_vd, _vd*	d-составляющая напряжения d-составляющая напряжения команды
_vq _vq*	q-составляющая напряжения команда q-axis voltage
_va, _vb, _vc	Фазы статора a, b, c напряжений
_ia, _ib, _ic	Фазы статора a, b, c токи

Контроллер скорости

Чтобы реализовать контроллер скорости, выберите параметр Control Type Speed Control. Если вы выбираете параметр Control Type Torque Controlблок не реализует контроллер скорости.

Контроллер скорости определяет команду крутящего момента, реализуя фильтр состояния и вычисляя команды feedforward и обратной связи. Если вы не реализуете контроллер скорости, введите команду крутящего момента в блок Flux Based PM Controller.

Фильтр состояния

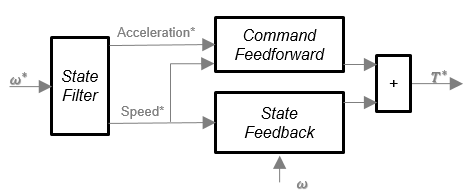
Фильтр состояния является lowpass фильтром, который генерирует команду ускорения на основе команды скорости. Дискретная форма характеристического уравнения задается:

$z + K_{s f} T_{s m} - 1$

Фильтр вычисляет коэффициент усиления, используя это уравнение.

$K_{s f} = \frac{1 - \exp (- T_{s m} 2 π E V_{s f})}{T_{s m}}$

В уравнениях используются эти переменные.

_EVsf	Шумовая полоса командного фильтра скорости
_Tsm	Устройство управления движением шага расчета
_Ksf	Постоянная времени регулятора скорости

Обратная связь о состоянии

Чтобы сгенерировать крутящий момент обратной связи состояния, блок использует отфильтрованный сигнал ошибки скорости от фильтра состояния. Чтобы фильтровать скорость, блок использует пропорциональный интегральный (PI) контроллер.

$T_{c m d} = K p_{ω} (ω_{m}^{*} - ω_{m}) + K i_{ω} \frac{z T_{s m}}{z - 1} (ω_{m}^{*} - ω_{m})$

В уравнениях используются эти переменные.

_ωm	Скорость ротора
_ωm*	Команда скорости ротора
_Tcmd	Команда крутящего момента
_Kpω	Пропорциональная составляющая регулятора скорости
_Kiω	Интегральная составляющая регулятора скорости
_Tsm	Выборка регулятора скорости

Командный Feedforward

Чтобы сгенерировать крутящий момент с прямой связью состояний, блок использует фильтрованные скорость и ускорение от фильтра с прямой связью состояний. Кроме того, при вычислении крутящего момента с прямой связью используются инерция, вязкое демпфирование и статическое трение. Чтобы достичь нулевой ошибки отслеживания, команда крутящего момента является суммой команд крутящего момента с feedforward и обратной связью.

Команда крутящего момента с прямой связью использует это уравнение.

$T_{c m d_f f} = J_{p} {\dot{ω}}_{m} + F_{v} ω_{m} + F_{s} \frac{ω_{m}}{| ω_{m} |}$

где:

_Jp	Инерция ротора
_{Tcmd_ff}	Команда крутящего момента с feedforward
_Fs	Статический крутящий момент трения
_Fv	Вязкий крутящий момент трения, константа
_Fs	Статический крутящий момент трения
_ωm	Скорость ротора

Текущая команда

Блок использует интерполяционные таблицы, чтобы определить команды тока по оси D и оси Q. Интерполяционные таблицы являются функциями механической скорости и крутящего момента. Чтобы определить интерполяционные таблицы, можно использовать внешние модели анализа конечных элементов (FEA) или результаты тестирования динамометра.

$\begin{array}{l} i_{d r e f} = f (| ω_{m} |, | T_{r e f} |) \\ i_{q r e f} = s i g n (T_{r e f}) * f (| ω_{m} |, | T_{r e f} |) \end{array}$

В уравнениях используются эти переменные.

_ωm	Скорость ротора
_Tref	Команда крутящего момента
_idref, _iqref	d- и q-составляющие опорного тока, соответственно

Команда напряжения

Блок использует эти уравнения, чтобы вычислить напряжение в исходной системе координат мотора.

$\begin{array}{l} v_{d} = \frac{d ψ_{d}}{d t} + R_{s} i_{d} - ω_{e} ψ_{q} \\ v_{q} = \frac{d ψ_{q}}{d t} + R_{s} i_{q} + ω_{e} ψ_{d} \end{array}$

$\begin{array}{l} \frac{d ψ_{d}}{d t} + R_{s} i_{d} = K p_{d} (i_{d}^{*} - i_{d}) + K i_{d} \frac{z T_{s t}}{z - 1} (i_{d}^{*} - i_{d}) \\ \frac{d ψ_{q}}{d t} + R_{s} i_{q} = K p_{q} (i_{q}^{*} - i_{q}) + K i_{q} \frac{z T_{s t}}{z - 1} (i_{q}^{*} - i_{q}) \\ v_{d} = K p_{i} (i_{d}^{*} - i_{d}) + K i_{d} \frac{z T_{s t}}{z - 1} (i_{d}^{*} - i_{d}) + ω_{e} ψ_{q} \\ v_{q} = K p_{i} (i_{q}^{*} - i_{q}) + K i_{q} \frac{z T_{s t}}{z - 1} (i_{q}^{*} - i_{q}) - ω_{e} ψ_{d} \\ ψ_{q} = f (i_{d}, i_{q}) \\ ψ_{d} = f (i_{d}, i_{q}) \end{array}$

В уравнениях используются эти переменные.

_ωm	Механическая скорость ротора
_ωe	Электрическая скорость ротора
_Rs, _Rr	Сопротивление обмоток статора и ротора, соответственно
_iq, _id	ток q- и d-осей, соответственно
_vq, _vd	q- и d-напряжения, соответственно
_Ψq, _Ψd	q- и d-составляющие потоки магнитов, соответственно
_Tst	Выборка регулятора тока
_Kid , _Kiq	d- и q- оси интегральной составляющей, соответственно
_Kpd , _Kpq	d- и q- оси пропорциональной составляющей, соответственно

Преобразовывает

Чтобы вычислить напряжения и токи в сбалансированных трехфазных (a, b) величинах, квадратурных двухфазных (α, β) величинах и вращающихся (d, q) опорных системах координат, блок использует Преобразования Кларка и Парка.

В уравнениях преобразования.

$\begin{array}{l} ω_{e} = P ω_{m} \\ \frac{d θ_{e}}{d t} = ω_{e} \end{array}$

Преобразовать	Описание	Уравнения
Кларк	Преобразует сбалансированные трехфазные величины (a, b) в сбалансированные двухфазные квадратурные величины (α, β).	$\begin{array}{l} x_{α} = \frac{2}{3} x_{a} - \frac{1}{3} x_{b} - \frac{1}{3} x_{c} \\ x_{β} = \frac{\sqrt{3}}{2} x_{b} - \frac{\sqrt{3}}{2} x_{c} \end{array}$
Парк	Преобразует сбалансированные двухфазные ортогональные стационарные величины (α, β) в ортогональную вращающуюся опорную систему координат (d, q).	$\begin{array}{l} x_{d} = x_{α} \cos θ_{e} + x_{β} \sin θ_{e} \\ x_{q} = - x_{α} \sin θ_{e} + x_{β} \cos θ_{e} \end{array}$
Обратный Кларк	Преобразует сбалансированные двухфазные квадратурные величины (α, β) в сбалансированные трехфазные величины (a, b).	$\begin{array}{l} x_{a} = x_{a} \\ x_{b} = - \frac{1}{2} x_{α} + \frac{\sqrt{3}}{2} x_{β} \\ x_{c} = - \frac{1}{2} x_{α} - \frac{\sqrt{3}}{2} x_{β} \end{array}$
Обратный парк	Преобразует ортогональную вращающуюся опорную систему координат (d, q) в сбалансированные двухфазные ортогональные стационарные величины (α, β).	$\begin{array}{l} x_{α} = x_{d} \cos θ_{e} - x_{q} \sin θ_{e} \\ x_{β} = x_{d} \sin θ_{e} + x_{q} \cos θ_{e} \end{array}$

Преобразования используют эти переменные.

_ωm	Скорость ротора
P	Пары полюсов ротора
_ωe	Электрическая скорость ротора
_Θe	Электрический угол ротора
x	Ток фазы или напряжение

Двигатель

Блок использует токи фазы и напряжения фазы, чтобы оценить ток шины постоянного тока. Положительный ток указывает на разряд батареи. Отрицательный ток указывает на заряд батареи.

Блок использует эти уравнения.

Загрузка степени	$L d_{P w r} = v_{a} i_{a} + v_{b} i_{b} + v_{c} i_{c}$
Исходный код степени	$S r c_{P w r} = L d_{P w r} + P w r_{L o s s}$
Ток шины постоянного тока	$i_{b u s} = \frac{S r c_{P w r}}{v_{b u s}}$
Расчетный крутящий момент ротора	$T_{e} = 1.5 P [ψ_{d} i_{q} - ψ_{q} i_{d}]$
Потеря степени для одного источника эффективности для загрузки	$P w r_{L o s s} = \frac{100 - E f f}{E f f} \cdot L d_{P w r}$
Потеря степени для одной нагрузки эффективности к источнику	$P w r_{L o s s} = \frac{100 - E f f}{100} \cdot \| L d_{P w r} \|$
Потери степени для табличной эффективности	$P w r_{L o s s} = f (ω_{m}, M t r T r q_{e s t})$

В уравнениях используются эти переменные.

_va, _vb, _vc	Фазы статора a, b, c напряжений
_vbus	Расчетное напряжение шины постоянного тока
_ia, _ib, _ic	Фазы статора a, b, c токи
_ibus	Расчетный ток шины постоянного тока
Eff	Общая эффективность инвертора
_ωm	Механическая скорость ротора
_Lq, _Ld	q- и d-составляющие индуктивность обмотки, соответственно
_Ψq, _Ψd	q- и d-составляющие потоки магнитов, соответственно
_iq, _id	ток q- и d-осей, соответственно
λ	Потоки постоянных магнитов редактирования
P	Пары полюсов ротора

Электрические потери

Чтобы задать электрические потери, на вкладке Electrical Losses, для Parameterize losses by, выберите одну из следующих опций.

Настройка Реализация блока

Настройка	Реализация блока
`Single efficiency measurement`	Электрические потери, рассчитанные с использованием постоянного значения для эффективности инвертора.
`Tabulated loss data`	Электрические потери, рассчитанные как функция от скоростей двигателя и крутящих моментов нагрузки.
`Tabulated efficiency data`	Электрические потери, рассчитанные с использованием эффективности инвертора, который является функцией скоростей двигателя и крутящих моментов нагрузки. Преобразует значения эффективность, которые вы обеспечиваете, в потери и использует табличные потери для симуляции. Игнорирует значения эффективность, которые вы обеспечиваете для нулевой скорости или нулевого крутящего момента. Потери приняты нулем, когда крутящий момент или скорость равны нулю. Использует линейную интерполяцию для определения потерь. Предоставьте табличные данные для низких скоростей и низких крутящих моментов, по мере необходимости, чтобы получить требуемый уровень точности для более низких условий степени. Не экстраполирует значения потерь для величин скорости и крутящего момента, которые превышают область значений таблицы.

Single efficiency measurement

Электрические потери, рассчитанные с использованием постоянного значения для эффективности инвертора.

Tabulated loss data

Электрические потери, рассчитанные как функция от скоростей двигателя и крутящих моментов нагрузки.

Tabulated efficiency data

Электрические потери, рассчитанные с использованием эффективности инвертора, который является функцией скоростей двигателя и крутящих моментов нагрузки.

Преобразует значения эффективность, которые вы обеспечиваете, в потери и использует табличные потери для симуляции.
Игнорирует значения эффективность, которые вы обеспечиваете для нулевой скорости или нулевого крутящего момента. Потери приняты нулем, когда крутящий момент или скорость равны нулю.
Использует линейную интерполяцию для определения потерь. Предоставьте табличные данные для низких скоростей и низких крутящих моментов, по мере необходимости, чтобы получить требуемый уровень точности для более низких условий степени.
Не экстраполирует значения потерь для величин скорости и крутящего момента, которые превышают область значений таблицы.

Для наилучшей практики используйте Tabulated loss data вместо Tabulated efficiency data:

Эффективность становится плохо заданным для нулевой скорости или нулевого крутящего момента.
Вы можете принять во внимание фиксированные потери, которые все еще присутствуют для нулевой скорости или крутящего момента.

Порты

Вход

расширить все

`SpdReq` - Команда скорости ротора
`scalar`

Команда скорости ротора, _ω*m, в рад/с.

Зависимости

Чтобы создать этот порт, выберите Speed Control для параметра Control Type.

`TrqCmd` - Команда крутящего момента
`scalar`

Команда крутящего момента, T*, в Н· м.

Зависимости

Чтобы создать этот порт, выберите Torque Control для параметра Control Type.

`BusVolt` - Напряжение шины постоянного тока
`scalar`

Напряжение шины постоянного тока, _vbus, в В.

`PhaseCurrA` - Ток
`scalar`

Фаза а тока статора, _ia, в А.

`PhaseCurrB` - Ток
`scalar`

Фаза тока статора b, _ib, в А.

`SpdFdbk` - Скорость ротора
`scalar`

Скорость ротора, _ωm, в рад/с.

`PosFdbk` - Электрический угол ротора
`scalar`

Электрический угол ротора, _Θm, в рад.

Выход

расширить все

`Info` - Сигнал шины
автобус

Сигнал шины, содержащий эти вычисления блоков.

Сигнал	Описание	Модули
`SrcPwr`	Исходный код степени	W
`LdPwr`	Загрузка степени	W
`PwrLoss`	Потеря степени	W
`MtrTrqEst`	Расчетный крутящий момент двигателя	Н· м

`BusCurr` - Ток шины
`scalar`

Расчетный ток шины постоянного тока, _ibus, в А.

`PhaseVolt` - Контактные напряжения статора
`array`

Напряжения на клеммах статора, _Va, _Vb и _Vc, в В.

Параметры

расширить все

Опции блока

`Control Type` - Выберите управление
`Torque Control` (по умолчанию) | `Speed Control`

Если вы выбираете Torque Controlблок не реализует контроллер скорости.

В этой таблице представлены строения портов.

Строение порта	Создает порты
`Speed Control`	`SpdReq`
`Torque Control`	`TrqCmd`

Параметры двигателя

`Number of pole pairs, PolePairs` - Поляки
`4` (по умолчанию) | `scalar`

Пары шестов двигателей, P.

`Vector of d-axis current breakpoints, id_index` - Ток
`vector`

d-составляющая тока, _{id_index}, в А.

`Vector of q-axis current breakpoints, iq_index` - ток
`vector`

q-составляющая тока, _{iq_index}, в А.

`Corresponding d-axis flux, lambda_d` - Поток
`vector`

d-составляющая потока, _λd, в Wb.

`Corresponding q-axis flux, lambda_q` - Поток
`vector`

q-составляющая потока, _λq, в Wb.

Токовый контроллер

`Sample time for the torque control, Tst` - Время
`1e-4` (по умолчанию) | `scalar`

Крутящий момент управляет шагом расчета, _Tst, в с.

`D-axis proportional gain, Kp_d` - Коэффициент усиления
`2.4056` (по умолчанию) | `scalar`

d-составляющая пропорциональная составляющая, _Kpd, в V/A.

`Q-axis proportional gain, Kp_q` - Коэффициент усиления
`2.4056` (по умолчанию) | `scalar`

q-составляющая пропорциональная составляющая, _Kpq, в V/A.

`D-axis integral gain, Ki_d` - Коэффициент усиления
`192.45` (по умолчанию) | `scalar`

d-составляющая интегральной составляющей, _Kid, в V/A· s.

`Q-axis integral gain, Ki_q` - Коэффициент усиления
`192.45` (по умолчанию) | `scalar`

q- интегральная составляющая оси, _Kiq, в V/A· s.

`Vector of speed breakpoints, wpb` - Точки останова
`vector`

Точки останова скорости, _ωbp, в рад/с.

`Vector of torque breakpoints, tpb` - Точки останова
`vector`

Точки останова крутящего момента, _Tbp, в Н· м.

`Corresponding d-axis current reference, id_ref` - Ток
`vector`

d-составляющая опорного тока, _idref, в А.

`Corresponding q-axis current reference, iq_ref` - Ток
`vector`

q-составляющая опорного тока, _iqref, в А.

Контроллер скорости