comm.LinearEqualizer
Выравнивание модулированных сигналов с помощью линейной фильтрации
Описание
The comm.LinearEqualizer Система object™ использует линейную линию задержки отвода фильтра с взвешенной суммой, чтобы выровнять модулированные сигналы, переданные через дисперсионный канал. Объект эквалайзера адаптивно настраивает веса отводов на основе выбранного алгоритма. Для получения дополнительной информации см. «Алгоритмы».
Для выравнивания модулированных сигналов с помощью линейного фильтра:
Создайте
comm.LinearEqualizerОбъекту и установите его свойства.Вызывайте объект с аргументами, как будто это функция.
Дополнительные сведения о работе системных объектов см. в разделе «Что такое системные объекты?».
Создание
Описание
lineq = comm.LinearEqualizer
lineq = comm.LinearEqualizer(Name,Value)comm.LinearEqualizer('Algorithm','RLS') конфигурирует объект эквалайзера для обновления весов отводов с помощью рекурсивного алгоритма наименьших квадратов (RLS). Заключайте каждое имя свойства в кавычки.
Свойства
Использование
Описание
y = lineq(x,tsym,tf)tf. Обучение Системного объекта начинает, когда tf изменения от false на true (на переднем ребре). Системный объект обучается до тех пор, пока все символы не будут tsym обрабатываются. Область входа tsym игнорируется, когда tf является false. Чтобы включить этот синтаксис, задайте значение свойства Algorithm 'LMS' или 'RLS' и свойство TrainingFlagInportPort в true.
y = lineq(x,aw)aw. Системный объект адаптирует веса ответвлений эквалайзера при aw является true. Если aw является falseСистемный объект сохраняет веса неизменными. Чтобы включить этот синтаксис, задайте значение свойства Algorithm 'CMA' и свойство AdaptWeightsSource к 'Input port'.
Входные параметры
Выходные аргументы
Функции объекта
Чтобы использовать функцию объекта, задайте системный объект в качестве первого входного параметра. Например, чтобы освободить системные ресурсы системного объекта с именем obj, используйте следующий синтаксис:
release(obj)
Примеры
Линейно выравнивание BPSK-модулированного сигнала
Создайте модулятор BPSK и систему object™ эквалайзера, задающую линейный эквалайзер LMS, имеющий восемь отводов и размер шага 0,03.
bpsk = comm.BPSKModulator; eqlms = comm.LinearEqualizer('Algorithm','LMS','NumTaps',8,'StepSize',0.03);
Измените ссылочный индекс отвода эквалайзера.
eqlms.ReferenceTap = 4;
Создайте набор тестовых данных. Получите данные путем свертки сигнала.
x = bpsk(randi([0 1],1000,1)); rxsig = conv(x,[1 0.8 0.3]);
Использование maxstep для поиска максимально допустимого размера шага.
mxStep = maxstep(eqlms,rxsig)
mxStep = 0.1384
Выравнивание принимаемого сигнала. Используйте первые 200 символов в качестве обучающей последовательности.
y = eqlms(rxsig,x(1:200));
Линейно выравнивание сигнала QPSK
Примените линейную эквализацию с помощью алгоритма наименьших средних квадратов (LMS), чтобы восстановить символы QPSK, прошедшие через многолучевой канал AWGN.
Инициализируйте переменные симуляции.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
chtaps = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];Сгенерируйте модулированные QPSK символы. Примените многолучевую фильтрацию каналов и искажения AWGN к символам.
data = randi([0 M-1],numSymbols,1);
tx = pskmod(data,M,pi/4);
rx = awgn(filter(chtaps,1,tx),25,'measured');Создайте линейный эквалайзер Системного объекта и отобразите строение по умолчанию. Отрегулируйте ссылочное касание так 1. Проверьте максимально допустимый размер шага. Выравнивание нарушенных символов.
eq = comm.LinearEqualizer
eq =
comm.LinearEqualizer with properties:
Algorithm: 'LMS'
NumTaps: 5
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
eq.ReferenceTap = 1; mxStep = maxstep(eq,rx)
mxStep = 0.3154
[y,err,weights] = eq(rx,tx(1:numTrainingSymbols));
Постройте график созвездия нарушенных и уравненных символов.
constell = comm.ConstellationDiagram('NumInputPorts',2);
constell(rx,y)
Постройте график сигнала ошибки эквалайзера и вычислите величину вектора ошибок (EVM) уравненных символов.
plot(abs(err)) grid on; xlabel('Symbols'); ylabel('|e|');title('Equalizer Error Signal')
errevm = comm.EVM; evm = errevm(tx,y)
evm = 11.7710
Постройте график весов отводов эквалайзера.
subplot(3,1,1); stem(real(weights)); ylabel('real(weights)'); xlabel('Tap'); grid on; axis([0 6 -0.5 1]) title('Equalizer Tap Weights') subplot(3,1,2); stem(imag(weights)); ylabel('imag(weights)'); xlabel('Tap'); grid on; axis([0 6 -0.5 1]) subplot(3,1,3); stem(abs(weights)); ylabel('abs(weights)'); xlabel('Tap'); grid on; axis([0 6 -0.5 1])
Линейно выравнивайте систему при помощи различных схем обучения
Продемонстрировать линейную эквализацию с помощью алгоритма наименьших средних квадратов (LMS), чтобы восстановить символы QPSK, прошедшие через канал AWGN. Примените различные схемы обучения эквалайзера и отобразите величину ошибки символа.
Setup системы
Симулируйте систему с QPSK-модуляцией, удовлетворяющую AWGN. Передайте пакеты, состоящие из 200 обучающих символов и 1800 случайных символов данных. Сконфигурируйте линейный эквалайзер LMS, чтобы восстановить пакетные данные.
M = 4; numTrainSymbols = 200; numDataSymbols = 1800; SNR = 20; trainingSymbols = pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4); numPkts = 10; lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',5,'ReferenceTap',3,'StepSize',0.01);
Обучите эквалайзер в начале каждого пакета с сбросом
Используйте предварительно обработанные обучающие символы при обработке каждого пакета. После обработки каждого пакета сбросьте эквалайзер. Этот сброс заставляет эквалайзер обучать отводы без предыдущего знания. Сигнал ошибки эквалайзера, графиков для первого, второго и последнего пакета, показывает более высокие символьные ошибки в начале каждого пакета.
jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; rx = awgn(packet,SNR); [~,err] = lineq(rx,trainingSymbols); reset(lineq) if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) title(['Packet # ',num2str(ii)]) xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on; jj = jj+1; end end
Обучите эквалайзер в начале каждого пакета без сброса
Обработайте каждый пакет с помощью предварительно настроенных обучающих символов. Не сбрасывайте эквалайзер после обработки каждого пакета. Не сбрасывая после каждого пакета, эквалайзер сохраняет веса отводов от обучающих предыдущих пакетов. Сигнал ошибки эквалайзера, графиков для первого, второго и последнего пакета, показывает, что после начального обучения на первом пакете последующие пакеты имеют меньше символьных ошибок в начале каждого пакета.
release(lineq) jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; channel = 1; rx = awgn(packet*channel,SNR); [~,err] = lineq(rx,trainingSymbols); if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) title(['Packet # ',num2str(ii)]) xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on; jj = jj+1; end end
Периодическое обучение эквалайзера
Системы с сигналами, подверженными изменяющимся во времени каналам, требуют периодического обучения эквалайзера для поддержания блокировки изменений канала. Задайте систему, которая имеет 200 символов обучения на каждые 1800 символов данных. Между обучением эквалайзер не обновляет веса касаний. Эквалайзер обрабатывает 200 символов на пакет.
Rs = 1e6;
fd = 20;
spp = 200; % Symbols per packet
b = randi([0 M-1],numDataSymbols,1);
dataSym = pskmod(b,M,pi/4);
packet = [trainingSymbols; dataSym];
stream = repmat(packet,10,1);
tx = (0:length(stream)-1)'/Rs;
channel = exp(1i*2*pi*fd*tx);
rx = awgn(stream.*channel,SNR);Установите AdaptAfterTraining свойство к false для остановки обновления веса отвода эквалайзера после фазы обучения.
release(lineq) lineq.AdaptAfterTraining = false
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'LMS'
NumTaps: 5
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: false
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
Выравнивание нарушенных данных. Постройте график угловой ошибки из канала, сигнала ошибки эквалайзера и сигнального созвездия. Когда канал изменяется, выход эквалайзера не удаляет эффекты канала. Созвездие выхода вращается вне синхронизации, что приводит к битовым ошибкам.
[y,err] = lineq(rx,trainingSymbols); figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('Time (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(err)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel Without Retraining')
scatterplot(y)
Установите TrainingInputPort свойство к true чтобы сконфигурировать эквалайзер, чтобы переобучить отводы при сигнализации trainFlag вход. Эквалайзер тренируется только тогда, когда trainFlag является true. После каждого 2000 символов эквалайзер переобучает отводы и сохраняет блокировку изменений канала. Постройте график угловой ошибки из канала, сигнала ошибки эквалайзера и сигнального созвездия. Когда канал изменяется, выход эквалайзера удаляет эффекты канала. Выходное созвездие не вращается вне синхронизации, и битовые ошибки уменьшаются.
release(lineq) lineq.TrainingFlagInputPort = true; symbolCnt = 0; numPackets = length(rx)/spp; trainFlag = true; trainingPeriod = 2000; eVec = zeros(size(rx)); yVec = zeros(size(rx)); for p=1:numPackets [yVec((p-1)*spp+1:p*spp,1),eVec((p-1)*spp+1:p*spp,1)] = ... lineq(rx((p-1)*spp+1:p*spp,1),trainingSymbols,trainFlag); symbolCnt = symbolCnt + spp; if symbolCnt >= trainingPeriod trainFlag = true; symbolCnt = 0; else trainFlag = false; end end figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('t (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(eVec)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel With Retraining')
scatterplot(yVec)
Линейно выравнивание задержанного сигнала
Симулируйте систему с задержкой между переданными символами и принятыми выборками. Типичные системы имеют фильтры передатчика и приемника, которые приводят к задержке. Эта задержка должна быть учтена для синхронизации системы. В этом примере системная задержка вводится без фильтров передачи и приема. Линейная эквализация, используя алгоритм наименьших средних квадратов (LMS), восстанавливает символы QPSK.
Инициализируйте переменные симуляции.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
mpChan = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];
systemDelay = dsp.Delay(20);
snr = 24;Сгенерируйте модулированные QPSK символы. Примените многолучевую фильтрацию канала, системную задержку и AWGN к переданным символам.
data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); % OQPSK delayedSym = systemDelay(filter(mpChan,1,tx)); rx = awgn(delayedSym,snr,'measured');
Создайте объекты equalizer и EVM System. Системный объект задает линейный эквалайзер, который использует LMS-алгоритм.
lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',9,'ReferenceTap',5); evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation');
Выравнивание без корректировки входной задержки
Выравнивание полученных символов.
[y1,err1,wts1] = lineq(rx,tx(1:numTrainingSymbols,1));
Найдите задержку между принятыми символами и переданными символами с помощью finddelay функция.
rxDelay = finddelay(tx,rx)
rxDelay = 20
Отображение информации об эквалайзере. Значение задержки указывает задержку, введенную эквалайзером. Вычислим общую задержку как сумму rxDelay и задержку эквалайзера.
eqInfo = info(lineq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency;
Пока выход эквалайзера не сходится, вероятность ошибки символа высока. Постройте график выхода ошибки, err1, чтобы определить, когда выровненный выход сходится.
plot(abs(err1)) xlabel('Symbols') ylabel('Error Magnitude') title('Equalizer Error Signal')
График показывает чрезмерные ошибки после периода обучения 1000 символов. При демодуляции символов и вычислении ошибок символов, для расчета безсовпадающего вывода и системной задержки между выходом эквалайзера и переданными символами, пропустите первые 2000 символов.
dataRec1 = pskdemod(y1(2000+totalDelay:end),M,pi/4); symErrWithDelay = symerr(data(2000:end-totalDelay),dataRec1)
symErrWithDelay = 5999
evmWithDelay = evm(y1)
evmWithDelay = 29.5795
Вероятность ошибок и EVM высоки, потому что задержка приема не была учтена в Системный объект эквалайзера.
Настройте входную задержку в эквалайзере
Выравнивание полученных данных при помощи значения задержки для установки InputDelay свойство. Потому что InputDelay является свойством nontunable, вы должны освободить lineq Системный объект для перенастройки InputDelay свойство. Выравнивание полученных символов.
release(lineq) lineq.InputDelay = rxDelay
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'LMS'
NumTaps: 9
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 5
InputDelay: 20
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
[y2,err2,wts2] = lineq(rx,tx(1:numTrainingSymbols,1));
Постройте график весов отвода и выровненной величины ошибки. A диаграммы лист-ствол показывает веса отводов эквалайзера до и после удаления системной задержки. A 2D графика показывает более медленное сходимость эквалайзера для задержанного сигнала по сравнению с сигналом с удаленной задержкой.
subplot(2,1,1) stem([real(wts1),real(wts2)]) xlabel('Taps') ylabel('Tap Weight Real') legend('rxDelayed','rxDelayRemoved') grid on subplot(2,1,2) stem([imag(wts1),imag(wts2)]) xlabel('Taps') ylabel('Tap Weight Imaginary') legend('rxDelayed','rxDelayRemoved') grid on
figure plot([abs(err1),abs(err2)]) xlabel('Symbols') ylabel('Error Magnitude') legend('rxDelayed','rxDelayRemoved') grid on
Постройте выход ошибок уравненных сигналов, rxDelayed и rxDelayRemoved. Для сигнала, который имеет удаленную задержку, эквалайзер сходится в течение периода обучения 1000 символов. При демодуляции символов и вычислении ошибок символов, для расчета безсовпадающего вывода и системной задержки между выходом эквалайзера и переданными символами, пропустите первые 500 символов. Перенастройка эквалайзера с учетом задержки системы позволяет лучше выравнивать сигнал и уменьшает ошибки символов и EVM.
eqInfo = info(lineq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency; dataRec2 = pskdemod(y2(500+totalDelay:end),M,pi/4); symErrDelayRemoved = symerr(data(500:end-totalDelay),dataRec2)
symErrDelayRemoved = 0
evmDelayRemoved = evm(y2(500+totalDelay:end))
evmDelayRemoved = 9.4435
Линейно выравнивайте символы при помощи обучения на основе EVM
Восстановите символы QPSK с помощью линейного эквалайзера с помощью обучения ответвлений на основе постоянных модулей (CMA) и EVM. При использовании алгоритмов слепого эквалайзера, таких как CMA, обучите отводы эквалайзера при помощи AdaptWeights свойство для запуска и остановки обучения. Функции Helper используются для генерации графиков и применения фазы коррекции.
Инициализируйте системные переменные.
rng(123456); M = 4; % QPSK numSymbols = 100; numPackets = 5000; raylChan = comm.RayleighChannel('PathDelays',[0 1], ... 'AveragePathGains',[0 -12],'MaximumDopplerShift',1e-5); SNR = 50; adaptWeights = true;
Создайте объекты equalizer и EVM System. Системный объект задает линейный эквалайзер при помощи адаптивного алгоритма CMA. Вызовите функцию helper, чтобы инициализировать графики рисунков.
lineq = comm.LinearEqualizer('Algorithm','CMA', ... 'NumTaps',5,'ReferenceTap',3, ... 'StepSize',0.03,'AdaptWeightsSource','Input port')
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'CMA'
NumTaps: 5
StepSize: 0.0300
Constellation: [1x4 double]
ReferenceTap: 3
InputSamplesPerSymbol: 1
AdaptWeightsSource: 'Input port'
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
info(lineq)
ans = struct with fields:
Latency: 2
evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation'); [errPlot,evmPlot,scatSym,adaptState] = initFigures(numPackets,lineq);
Эквализация Цикла
Для реализации цикла эквализации:
Сгенерируйте пакеты данных PSK.
Примените Релеевское замирание и AWGN к данным передачи.
Примените эквализацию к полученным данным и фазе коррекцию к выходу эквалайзера.
Оцените EVM и переключите
adaptWeightsфлаг вtrueилиfalseна основе уровня EVM.Обновите графики рисунков.
for p=1:numPackets data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); rx = awgn(raylChan(tx),SNR); rxDelay = finddelay(rx,tx); [y,err,wts] = lineq(rx,adaptWeights); y = phaseCorrection(y); evmEst = evm(y); adaptWeights = (evmEst > 20); updateFigures(errPlot,evmPlot,scatSym,adaptState, ... wts,y(end),evmEst,adaptWeights,p,numPackets) end
rxDelay
rxDelay = 0
Графики рисунка показывают, что, когда EVM изменяется, эквалайзер переключается и выходит из направленного на принятие решения режима адаптации веса.
Вспомогательные функции
Эта вспомогательная функция инициализирует рисунки, которые показывают квадратичный график результатов симуляции.
function [errPlot,evmPlot,scatter,adaptState] = initFigures(numPkts,lineq) yVec = nan(numPkts,1); evmVec = nan(numPkts,1); wVec = zeros(lineq.NumTaps,1); adaptVec = nan(numPkts,1); figure subplot(2,2,1) evmPlot = stem(wVec); grid on; axis([1 lineq.NumTaps 0 1.8]) xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2) scatter = plot(yVec, '.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on xlabel('In-phase'); ylabel('Quadrature'); title('Scatter Plot'); subplot(2,2,3) adaptState = plot(adaptVec); grid on; axis([0 numPkts -0.2 1.2]) ylabel('Training'); xlabel('Symbols'); title('Adapt Weights Signal') subplot(2,2,4) errPlot = plot(evmVec); grid on; axis([1 numPkts 0 100]) xlabel('Symbols'); ylabel('EVM (%)'); title('EVM') end
Эта вспомогательная функция обновляет рисунки.
function updateFigures(errPlot,evmPlot,scatSym, ... adaptState,w,y,evmEst,adaptWts,p,numFrames) persistent yVec evmVec adaptVec if p == 1 yVec = nan(numFrames,1); evmVec = nan(numFrames,1); adaptVec = nan(numFrames,1); end yVec(p) = y; evmVec(p) = evmEst; adaptVec(p) = adaptWts; errPlot.YData = abs(evmVec); evmPlot.YData = abs(w); scatSym.XData = real(yVec); scatSym.YData = imag(yVec); adaptState.YData = adaptVec; drawnow limitrate end
Эта вспомогательная функция применяет коррекцию фазы.
function y = phaseCorrection(y) a = angle(y((real(y) > 0) & (imag(y) > 0))); a(a < 0.1) = a(a < 0.1) + pi/2; theta = mean(a) - pi/4; y = y * exp(-1i*theta); end
Линейно выравнивайте пакетированные сигналы в окружениях с замираниями
Восстановите символы QPSK в затухающих окружениях с помощью линейного эквалайзера, используя алгоритм наименьших средних квадратов (LMS). Используйте reset функция объекта для выравнивания независимых пакетов. Используйте вспомогательные функции для генерации графиков. Этот пример также показывает обработку на основе символов и обработку на основе кадров.
Setup
Инициализируйте системные переменные, создайте Системный объект эквалайзера и инициализируйте рисунки графика.
M = 4; % QPSK numSym = 1000; numTrainingSym = 100; numPackets = 5; numTaps = 9; ttlNumSym = numSym + numTrainingSym; raylChan = comm.RayleighChannel('PathDelays',[0 1], ... 'AveragePathGains',[0 -9], ... 'MaximumDopplerShift',0, ... 'PathGainsOutputPort',true); SNR = 35; rxVec = zeros(ttlNumSym,numPackets); txVec = zeros(ttlNumSym,numPackets); yVec = zeros(ttlNumSym,1); eVec = zeros(ttlNumSym,1); lineq1 = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',numTaps,'ReferenceTap',5, ... 'StepSize',0.01,'TrainingFlagInputPort',true); [errPlot,wStem,hStem,scatPlot] = initFigures(ttlNumSym,lineq1, ... raylChan.AveragePathGains);
Символьная обработка
Для обработки на основе символов предоставьте один символ на входе эквалайзера. Сбросьте состояние эквалайзера и канала после обработки каждого пакета.
for p = 1:numPackets trainingFlag = true; for q=1:ttlNumSym data = randi([0 M-1],1,1); tx = pskmod(data,M,pi/4); [xc,pg] = raylChan(tx); rx = awgn(xc,25); [y,err,wts] = lineq1(rx,tx,trainingFlag);
Отключите обучение после обработки numTrainingSym обучающие символы.
if q == numTrainingSym trainingFlag = false; end updateFigures(errPlot,wStem,hStem,scatPlot,err,wts,y,pg,q,ttlNumSym); txVec(q,p) = tx; rxVec(q,p) = rx; end
После обработки каждого пакета сбрасывайте Системный объект канала, чтобы получить новую реализацию отводов канала, и Системный объект эквалайзера, чтобы восстановить набор весов отводов по умолчанию.
reset(raylChan)
reset(lineq1)
end
Пакетная обработка
Для обработки на основе пакетов предоставьте один пакет на входе эквалайзера. Каждый пакет содержит ttlNumSym символы. Поскольку длительность обучения меньше, чем длина пакета, вам не нужно задавать вход начального обучения.
yVecPkt = zeros(ttlNumSym,numPackets); errVecPkt = zeros(ttlNumSym,numPackets); wgtVecPkt = zeros(numTaps,numPackets); lineq2 = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',9,'ReferenceTap',6,'StepSize',0.01); for p = 1:numPackets [yVecPkt(:,p),errVecPkt(:,p),wgtVecPkt(:,p)] = ... lineq2(rxVec(:,p),txVec(1:numTrainingSym,p)); for q=1:ttlNumSym updateFigures(errPlot,wStem,hStem,scatPlot, ... errVecPkt(q,p),wgtVecPkt(:,p),yVecPkt(q,p),pg,q,ttlNumSym); end
После обработки каждого пакета сбрасывайте Системный объект канала, чтобы получить новую реализацию отводов канала, и Системный объект эквалайзера, чтобы восстановить набор весов отводов по умолчанию.
reset(raylChan)
reset(lineq2)
end
Вспомогательные функции
Функция helper инициализирует рисунки.
function [errPlot,wStem,hStem,scatPlot] = initFigures(ttlNumSym,lineq,pg) yVec = nan(ttlNumSym,1); eVec = nan(ttlNumSym,1); wVec = zeros(lineq.NumTaps,1); figure; subplot(2,2,1); wStem = stem(wVec); axis([1 lineq.NumTaps 0 1.8]); grid on xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2); hStem = stem([0 abs(pg) 0]); grid on; xlabel('Taps'); ylabel('|Path Gain|'); title('Channel Path Gain Magnitude') subplot(2,2,3); errPlot = plot(eVec); axis([1 ttlNumSym 0 1.2]); grid on xlabel('Symbols'); ylabel('|Error Magnitude|'); title('Error Magnitude') subplot(2,2,4); scatPlot = plot(yVec,'.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on; xlabel('In-phase'); ylabel('Quadrature'); title(sprintf('Scatter Plot')); end
Эта вспомогательная функция обновляет рисунки.
function updateFigures(errPlot,wStem,hStem,scatPlot, ... err,wts,y,pg,p,ttlNumSym) persistent yVec eVec if p == 1 yVec = nan(ttlNumSym,1); eVec = nan(ttlNumSym,1); end yVec(p) = y; eVec(p) = abs(err); errPlot.YData = abs(eVec); wStem.YData = abs(wts); hStem.YData = [0 abs(pg) 0]; scatPlot.XData = real(yVec); scatPlot.YData = imag(yVec); drawnow limitrate end
Неадаптивная линейная эквализация
Используйте линейный эквалайзер в неадаптивном режиме. Используйте mmseweights функция объекта, чтобы вычислить решение минимальной квадратичной невязки (MMSE) и использовать веса, возвращенные в качестве набора весов отвода для линейного эквалайзера.
Инициализируйте переменные симуляции.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
chtaps = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];
EbN0 = 20;Сгенерируйте модулированные символы QPSK. Примените к символам фильтр многолучевого распространения и искажения AWGN.
data = randi([0 M-1], numSymbols, 1);
tx = pskmod(data, M, pi/4);
rx = awgn(filter(chtaps,1,tx),25,'measured');Создайте линейный эквалайзер Системный объект, сконфигурированный для использования алгоритма CMA, установите AdaptWeights свойство к false, и InitialWeightsSource свойство к Property. Вычислите веса MMSE. Установите начальные веса отводов равными рассчитанным весам MMSE. Выравнивание нарушенных символов.
eq = comm.LinearEqualizer('Algorithm','CMA','AdaptWeights',false,'InitialWeightsSource','Property')
eq =
comm.LinearEqualizer with properties:
Algorithm: 'CMA'
NumTaps: 5
StepSize: 0.0100
Constellation: [1x4 double]
InputSamplesPerSymbol: 1
AdaptWeightsSource: 'Property'
AdaptWeights: false
InitialWeightsSource: 'Property'
InitialWeights: [5x1 double]
WeightUpdatePeriod: 1
wgts = mmseweights(eq,chtaps,EbN0)
wgts = 5×1 complex
0.0005 - 0.0068i
0.0103 + 0.0117i
0.9694 - 0.0019i
-0.3987 + 0.2186i
0.0389 - 0.1756i
eq.InitialWeights = wgts; [y,err,weights] = eq(rx);
Постройте созвездие нарушенных и уравненных символов.
constell = comm.ConstellationDiagram('NumInputPorts',2);
constell(rx,y)
Постройте график сигнала ошибки эквалайзера и вычислите величину вектора ошибок уравненных символов.
plot(abs(err)) grid on; xlabel('Symbols'); ylabel('|e|')
errevm = comm.EVM; evm = errevm(tx,y)
evm = 140.6177
Постройте график весов ответвлений эквалайзера.
subplot(3,1,1); stem(real(weights)); ylabel('real(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumTaps+0.5 eq.NumTaps+0.5], [-0.5 1], 'Color', 'r', 'LineWidth', 1) title('Equalizer Tap Weights') subplot(3,1,2); stem(imag(weights)); ylabel('imag(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumTaps+0.5 eq.NumTaps+0.5], [-0.5 1], 'Color', 'r', 'LineWidth', 1) subplot(3,1,3); stem(abs(weights)); ylabel('abs(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumTaps+0.5 eq.NumTaps+0.5], [-0.5 1], 'Color', 'r', 'LineWidth', 1)
Линейно выравнивайте частоту дискретизации сигналов
Продемонстрировать линейную эквализацию с помощью алгоритма наименьших средних квадратов (LMS), чтобы восстановить символы QPSK, прошедшие через канал AWGN. Обработайте дискретизацию сигнала по дискретизации.
Setup системы
Симулируйте систему с QPSK-модуляцией, удовлетворяющую AWGN. Передайте пакеты, состоящие из 200 обучающих символов и 1800 случайных символов данных. Сконфигурируйте линейный эквалайзер LMS, чтобы восстановить пакетные данные.
M = 4; numTrainSymbols = 200; numDataSymbols = 1800; SNR = 20; trainingSymbols = pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4); numPkts = 10; lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',5,'ReferenceTap',3,'StepSize',0.01,'TrainingFlagInputPort',true);
Основной цикл
Используйте предварительно обработанные обучающие символы при обработке каждого пакета. После обработки каждого пакета сбросьте эквалайзер. Этот сброс заставляет эквалайзер обучать отводы без предыдущего знания. Выравнивание полученного сигнала по дискретизации. Для каждого пакета используйте первые 200 символов для обучения.
subPlotCnt = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; rx = awgn(packet,SNR); y = zeros(numDataSymbols+numTrainSymbols,1); err = zeros(numDataSymbols+numTrainSymbols,1); for jj = 1:numDataSymbols+numTrainSymbols if jj <= numTrainSymbols [y(jj),err(jj)] = lineq(rx(jj),trainingSymbols(jj),true); else [y(jj),err(jj)] = lineq(rx(jj),1i,false); end end reset(lineq) if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,subPlotCnt) plot(abs(err)) title(['Packet # ',num2str(ii)]) xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on; subPlotCnt = subPlotCnt+1; end end
Линейно выравнивать пакет с использованием нескольких проходов
Продемонстрировать линейную эквализацию с помощью алгоритма наименьших средних квадратов (LMS), чтобы восстановить символы QPSK, прошедшие через канал AWGN. Обработайте пакет, который имеет обучающие символы в начале нескольких проходов. Сравните результаты с обработкой полного пакета эквализацией за один проход.
Setup системы
Симулируйте систему с QPSK-модуляцией, удовлетворяющую AWGN. Передайте пакеты, состоящие из 200 обучающих символов и 1800 случайных символов данных. Сконфигурируйте линейный эквалайзер LMS, чтобы восстановить пакетные данные.
M = 4; numTrainSymbols = 200; numDataSymbols = 1800; SNR = 20; trainingSymbols = pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4); b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; rx = awgn(packet,SNR); lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',5,'ReferenceTap',3,'StepSize',0.01);
Обработка пакета за один проход
Используйте предварительно обработанные обучающие символы при обработке каждого пакета. После обработки каждого пакета сбросьте эквалайзер. Этот сброс заставляет эквалайзер обучать отводы без предыдущего знания. Выравнивание полученного сигнала по дискретизации. Для каждого пакета используйте первые 200 символов для обучения.
subPlotCnt = 1; figure [y1,err1] = lineq(rx,trainingSymbols); reset(lineq) plot(abs(err1)) title("Single Pass Processing") xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on;
Обработка пакета несколькими проходами
Используйте предварительно обработанные обучающие символы при обработке каждого пакета. После обработки каждого пакета сбросьте эквалайзер. Этот сброс заставляет эквалайзер обучать отводы без предыдущего знания. Выравнивание полученного сигнала по дискретизации. Для каждого пакета используйте первые 200 символов для обучения.
lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',5,'ReferenceTap',3,'StepSize',0.01,'TrainingFlagInputPort',true); frameLen = 100; numFrames = (numDataSymbols+numTrainSymbols) / frameLen; figure y2 = zeros(numDataSymbols+numTrainSymbols,1); err2 = zeros(numDataSymbols+numTrainSymbols,1); idx = 1:frameLen; symbolCnt = 0; for jj = 1:numFrames if symbolCnt < numTrainSymbols [y2(idx),err2(idx)] = lineq(rx(idx),trainingSymbols(idx),true); else [y2(idx),err2(idx)] = lineq(rx(idx),1i*ones(frameLen,1),false); end idx = idx + frameLen; symbolCnt = symbolCnt + frameLen; end reset(lineq) plot(abs(err2)) title("Multipass Processing") xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on;
Результаты эквализации с использованием однопроходного и мультипасового подходов совпадают.
outputsEqual = isequal(y1,y2)
outputsEqual = logical
1
errorsEqual = isequal(err1,err2)
errorsEqual = logical
1
Подробнее о
Алгоритмы
Линейные эквалайзеры
Линейные эквалайзеры могут удалить межсимвольную интерференцию (ISI), когда частотная характеристика канала не имеет значения null. Если в частотной характеристики канала существует ядро, линейные эквалайзеры, как правило, усиливают шум. В этом случае используйте эквалайзеры обратной связи принятия решения, чтобы избежать усиления шума.
Линейный эквалайзер состоит из выделенной линии задержки, которая сохраняет выборки из входного сигнала. Один раз за период символа эквалайзер выводит взвешенную сумму значений в линии задержки и обновляет веса для подготовки к следующему периоду символа.
Линейные эквалайзеры могут быть разнесены по символам или разделены по дробям.
Для эквалайзера с разбиением на символы количество выборок на символ, K, равно 1. Скорость выхода выборки равна скорости входа выборки.
Для эквалайзера с дробным интервалом символов количество выборок на символ, K, является целым числом, большим 1. Обычно K равен 4 для фракционно разнесенных эквалайзеров. Выходная частота дискретизации 1/ T, и входная частота дискретизации K/T, где T - период символа. Обновление веса контакта происходит со скоростью выхода.
Эта схема показывает линейный эквалайзер с L весами, периодом T и K выборками на символ. Если K равно 1, результатом является линейный эквалайзер с разбиением на символы вместо линейного эквалайзера с разделением на фракции символов.
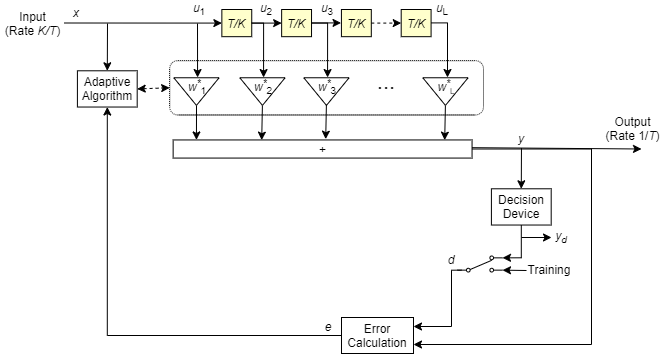
В каждом символьном периоде эквалайзер принимает K входных выборок на выделенной линии задержки. Затем эквалайзер выводит взвешенную сумму значений в выделенной линии задержки и обновляет веса, чтобы подготовиться к следующему периоду символа.
Для получения дополнительной информации см. «Эквализация».