Структуры адаптивного эквалайзера обеспечивают неоптимальную эквализацию временных изменений в характеристиках канала распространения. Однако эти эквалайзеры привлекательны, потому что их вычислительная сложность ниже, чем у эквалайзеров MLSE.
В Communications Toolbox™ comm.LinearEqualizer и comm.DecisionFeedbackEqualizer Системные объекты и блоки Linear Equalizer и Decision Feedback Equalizer используют фильтры линии запаздывания для выравнивания линейно модулированного сигнала через дисперсионный канал. Эти функции выводят оценку сигнала при помощи оценки канала, смоделированного как фильтр с конечной входной характеристикой (конечной импульсной характеристикой).
Чтобы декодировать принятый сигнал, адаптивный эквалайзер:
Применяет конечная импульсная характеристика к символам входного сигнала. Веса отводов конечной импульсной характеристики соответствуют оценке канала.
Выводит оценку сигнала и использует оценку сигнала, чтобы обновить веса отвода для следующего символа. Оценка сигнала и обновление весов зависят от структуры и алгоритма адаптивного эквалайзера.
Опции структуры адаптивного эквалайзера являются линейными или обратной связями с решением. Опции адаптивного алгоритма являются наименьшим средним квадратом (LMS), рекурсивным средним квадратом (RMS) или алгоритмом постоянного модуля (CMA). Для справочного материала по адаптивным эквалайзерам смотрите Selected References for Equalizers.
Для линейного эквалайзера количество отводов должно быть больше или равно количеству входа выборок на символ. Для эквалайзера обратной связи принятия решения количество прямых отводов должно быть больше или равным количеству входом отсчетов на символ.
Можно сконфигурировать эквалайзер так, чтобы он работал как эквалайзер с разбиением на символы или как эквалайзер с разделением на фракции символов.
Чтобы привести эквалайзер в действие со скоростью, разнесенной по символам, задайте количество выборок на символ следующим 1. Эквалайзеры со скоростью символов имеют отводы, разнесенные на длительность символа. Эквалайзеры со скоростью символов чувствительны к фазе синхронизации.
Чтобы управлять эквалайзером с разнесенной частотой дискретизации, задайте количество входа отсчетов на символ как целое число, больше 1 и обеспечивают входной сигнал с избыточной дискретизацией с этой частотой дискретизации. Дробные эквалайзеры с интервалами по символам имеют отводы, разнесенные на целую долю от длительности входного символа. Фракционные эквалайзеры с интервалами по символам не чувствительны к фазе синхронизации.
Примечание
Эквалайзер MLSE поддерживает дробный интервал символов, но его использование не рекомендуется. Вычислительная сложность и нагрузка MLSE растет экспоненциально с длиной временной дисперсии канала. Избыточная дискретизация входа означает умножение экспоненциального члена на количество выборок на символ.
Линейные эквалайзеры могут удалить межсимвольную интерференцию (ISI), когда частотная характеристика канала не имеет значения null. Если в частотной характеристики канала существует ядро, линейные эквалайзеры, как правило, усиливают шум. В этом случае используйте эквалайзеры обратной связи принятия решения, чтобы избежать усиления шума.
Линейный эквалайзер состоит из выделенной линии задержки, которая сохраняет выборки из входного сигнала. Один раз за период символа эквалайзер выводит взвешенную сумму значений в линии задержки и обновляет веса для подготовки к следующему периоду символа.
Линейные эквалайзеры могут быть разнесены по символам или разделены по дробям.
Для эквалайзера с разбиением на символы количество выборок на символ, K, равно 1. Скорость выхода выборки равна скорости входа выборки.
Для эквалайзера с дробным интервалом символов количество выборок на символ, K, является целым числом, большим 1. Обычно K равен 4 для фракционно разнесенных эквалайзеров. Выходная частота дискретизации 1/ T, и входная частота дискретизации K/T, где T - период символа. Обновление веса контакта происходит со скоростью выхода.
Эта схема показывает линейный эквалайзер с L весами, периодом T и K выборками на символ. Если K равно 1, результатом является линейный эквалайзер с разбиением на символы вместо линейного эквалайзера с разделением на фракции символов.
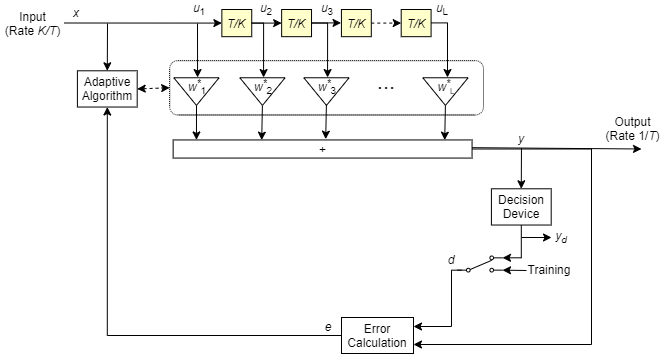
В каждом символьном периоде эквалайзер принимает K входных выборок на выделенной линии задержки. Затем эквалайзер выводит взвешенную сумму значений в выделенной линии задержки и обновляет веса, чтобы подготовиться к следующему периоду символа.
Эквалайзер с обратной связью принятия решения (DFE) является нелинейным эквалайзером, который уменьшает межсимвольную интерференцию (ISI) в частотно-избирательных каналах. Если null существует в частотной характеристики канала, DFE не усиливают шум. DFE состоит из выделенной линии задержки, которая сохраняет выборки из входного сигнала и содержит фильтр прямой связи и фильтр обратной связи. Прямой фильтр аналогичен линейному эквалайзеру. Фильтр обратной связи содержит отведенную линию задержки, входы которой являются решениями, принятыми по уравненному сигналу. Один раз за период символа эквалайзер выводит взвешенную сумму значений в линии задержки и обновляет веса для подготовки к следующему периоду символа.
DFE могут быть разнесены по символам или разнесены по фракциям.
Для эквалайзера с разбиением на символы количество выборок на символ, K, равно 1. Скорость выхода выборки равна скорости входа выборки.
Для эквалайзера с дробным интервалом символов количество выборок на символ, K, является целым числом, большим 1. Обычно K равен 4 для уравнителей с интервалами между символами. Выходная частота дискретизации 1/ T, и входная частота дискретизации K/T. Обновление веса касания происходит со скоростью выхода.
Эта схема показывает разнесенный по долям DFE с общим количеством N весов, периодом T и K выборок на символ. Фильтр имеет L веса вперед и N - L веса обратной связи. Прямой фильтр находится в верхней части, а фильтр обратной связи - в нижней части. Если K равно 1, результатом является разнесенный по символам DFE вместо разнесенного по фракциям DFE с символами.
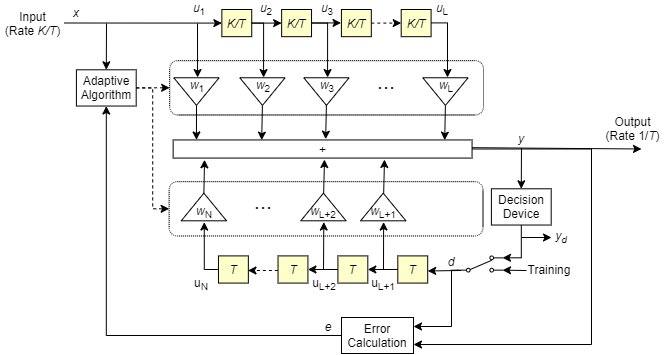
В каждом периоде символа эквалайзер принимает K входных выборок в прямом фильтре и одно решение или обучающую выборку в фильтре обратной связи. Затем эквалайзер выводит взвешенную сумму значений в линиях задержки прямой и обратной связи и обновляет веса для подготовки к следующему периоду символа.
Примечание
Алгоритм для блока Адаптивный Алгоритм в схеме совместно оптимизирует веса прямой и обратной связи. Оптимизация соединений особенно важна для сходимости в рекурсивном алгоритме наименьшего квадрата (RLS).
В приложениях по умолчанию эквалайзер сначала работает в режиме обучения, чтобы собрать информацию о канале. Эквалайзер позже переходит в режим, направленный на принятие решений.
Когда эквалайзер работает в режиме обучения, опорный сигнал является предустановленной, известной переданной последовательностью.
Когда эквалайзер работает в направленном на принятие решений режиме, опорный сигнал является обнаруженной версией сигнала выхода, обозначенной y d в схеме.
Алгоритм CMA не имеет режима обучения. Режим обучения применяется только, когда эквалайзер сконфигурирован для использования алгоритма LMS или RLS.
Операция вычисления ошибки генерирует сигнал, заданный этим выражением, где R является константой, связанной с сигнальным созвездием.
Для структур линейного эквалайзера и эквалайзера с обратной связью с решением выбор LMS, RLS или CMA определяет алгоритмы, которые используются, чтобы задать веса отводов и выполнить вычисление ошибки. Новый набор весов касаний зависит от:
Текущий набор весов касаний
Входной сигнал
Выходной сигнал
Опорный сигнал, d, только для адаптивных алгоритмов LMS и RLS. Характеристики опорного сигнала зависят от режима работы эквалайзера.
Для LMS-алгоритма в предыдущей схеме w является вектором всех весов wi, а u является вектором всех входов ui. На основе текущего набора весов LMS-алгоритм создает новый набор весов как
w new = w current + (StepSize) u e *.
Размер шага, используемый адаптивным алгоритмом, задается как положительная скалярная величина. Увеличение размера шага уменьшает время сходимости эквалайзера, но заставляет выравниваемый выходной сигнал быть менее стабильным. Чтобы определить максимальный размер шага, допустимый при использовании адаптивного алгоритма LMS, используйте maxstep функция объекта. Оператор * обозначает комплексный сопряженный и вычисление ошибки e = d - y.
Для алгоритма RLS, в предыдущей схеме, w является вектором всех весов wi, и u является вектором всех входов ui. Основываясь на текущем наборе входов, u и матрице обратной корреляции, P, алгоритм RLS сначала вычисляет вектор усиления Калмана, K, как
Коэффициент забывания, используемый адаптивным алгоритмом, задается как скаляр в области значений (0, 1]. Уменьшение коэффициента забывания уменьшает время сходимости эквалайзера, но приводит к меньшей устойчивости выравниваемого выходного сигнала. H обозначает гермитову транспозицию. На основе текущей обратной корреляционной матрицы, новая обратная корреляционная матрица
На основе текущего набора весов алгоритм RLS создает новый набор весов как
w new = w current + K * e.
Оператор * обозначает комплексный сопряженный и вычисление ошибки e = d - y.
Для адаптивного алгоритма CMA, в предыдущей схеме, w является вектором всех весов wi, и u является вектором всех входов ui. Основываясь на текущем наборе весов, адаптивный алгоритм CMA создает новый набор весов как
w new = w current + (StepSize) u * e.
Размер шага, используемый адаптивным алгоритмом, задается как положительная скалярная величина. Увеличение размера шага уменьшает время сходимости эквалайзера, но заставляет выравниваемый выходной сигнал быть менее стабильным. Чтобы определить максимальный размер шага, разрешенный адаптивным алгоритмом CMA, используйте maxstep функция объекта. Оператор * обозначает комплексный сопряженный и вычисление ошибки e = y (R - |<reservedrangesplaceholder0>|2), где R является константой, связанной с сигнальным созвездием.
Выберите структуру линейного эквалайзера или эквалайзера с обратной связью принятия решений. Решите, какой адаптивный алгоритм использовать - LMS, RLS или CMA. Задайте настройки для структуры и специфичных для алгоритма режимов работы.
Конфигурирование эквалайзера включает выбор линейной структуры или обратной связи с решением, выбор адаптивного алгоритма и определение структуры и конкретных режимов работы алгоритма.
При принятии решения о том, какой адаптивный алгоритм наилучшим образом соответствует вашим потребностям, примите во внимание:
LMS-алгоритм выполняется быстро, но сходится медленно. Его сложность линейно увеличивается с количеством весов.
Алгоритм RLS сходится быстро. Его сложность увеличивается приблизительно с квадратом числа весов. Этот алгоритм также может быть нестабильным, когда количество весов велико.
Алгоритм постоянного модуля (CMA) полезен, когда нет доступного обучающего сигнала. Это лучше всего работает для постоянных модуляций модуля, таких как PSK.
Если CMA не имеет дополнительной побочной информации, это может ввести неоднозначность фазы. Для примера веса, найденные CMA, могут создать идеальное созвездие QPSK, но ввести вращение фазы 90, 180 или 270 степеней. В этом случае используйте алгоритм коррекции неоднозначности фазы или выберите схему дифференциальной модуляции. Схемы дифференциальной модуляции нечувствительны к неоднозначности фазы.
Чтобы просмотреть или изменить любые свойства адаптивного эквалайзера, используйте синтаксис, описанный для объектов канала в Отображении и Изменении свойств объекта.
Для получения дополнительной информации об адаптивных алгоритмах см. Ссылки, перечисленные в разделе «Выбранные ссылки для эквалайзеров».
Чтобы создать адаптивный объект эквалайзера для использования в MATLAB®, выберите comm.LinearEqualizer или comm.DecisionFeedbackEqualizer Системные object™. Для Simulink®, используйте Linear Equalizer или Decision Feedback Equalizer блок. На основе характеристик канала распространения в вашей симуляции используйте критерии в Эквализацию, чтобы выбрать структуру эквалайзера.
Объект эквалайзера имеет много свойств, которые записывают информацию об эквалайзере. Свойства могут быть связаны с:
Структура эквалайзера, например количество отводов.
Адаптивный алгоритм, который использует эквалайзер, такой как размер шага в алгоритме LMS или CMA.
Информация о текущем состоянии эквалайзера. Объект эквалайзера может выводить значения весов.
Чтобы просмотреть или изменить любые свойства объекта эквалайзера, используйте синтаксис, описанный для объектов канала в Отображении и изменении свойств объекта.
Определение объекта эквалайзера
Код создает объекты эквалайзера для этих строений:
Линейный эквалайзер RLS с разбиением на символы с 10 весами.
Линейный эквалайзер RLS с фракционными интервалами с 10 весами, созвездием BPSK и двумя выборками на символ.
Эквалайзер RLS с обратной связью принятия решений с тремя весами в фильтре с feedforward и двумя весами в фильтре с обратной связью.
Все три объекта эквалайзера задают адаптивный алгоритм RLS с коэффициентом забывания 0,3.
Создайте объекты эквалайзера разных типов. Настройки по умолчанию используются для свойств, не заданных с помощью 'Name,Value' пар.
eqlin = comm.LinearEqualizer('Algorithm','RLS','NumTaps',10,'ForgettingFactor',0.3)
eqlin =
comm.LinearEqualizer with properties:
Algorithm: 'RLS'
NumTaps: 10
ForgettingFactor: 0.3000
InitialInverseCorrelationMatrix: 0.1000
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
eqfrac = comm.LinearEqualizer('Algorithm','RLS','NumTaps',10,'ForgettingFactor',0.3, ... 'Constellation',[-1 1],'InputSamplesPerSymbol',2)
eqfrac =
comm.LinearEqualizer with properties:
Algorithm: 'RLS'
NumTaps: 10
ForgettingFactor: 0.3000
InitialInverseCorrelationMatrix: 0.1000
Constellation: [-1 1]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 2
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
eqdfe = comm.DecisionFeedbackEqualizer('Algorithm','RLS','NumForwardTaps',3, ... 'NumFeedbackTaps',2,'ForgettingFactor',0.3)
eqdfe =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'RLS'
NumForwardTaps: 3
NumFeedbackTaps: 2
ForgettingFactor: 0.3000
InitialInverseCorrelationMatrix: 0.1000
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
Назначение адаптивного алгоритма
Используйте Algorithm свойство для назначения адаптивного алгоритма, используемого эквалайзером.
Назначение алгоритма
При создании объекта эквалайзера назначьте адаптивный алгоритм.
eqlms = comm.LinearEqualizer('Algorithm','LMS');
Создайте объект эквалайзера с настройками свойств по умолчанию. LMS является адаптивным алгоритмом по умолчанию.
eqrls = comm.LinearEqualizer; eqrls.Algorithm
ans = 'LMS'
Обновление eqrls для использования адаптивного алгоритма RLS.
eqrls.Algorithm = 'RLS';
eqrls.Algorithmans = 'RLS'
Клонирование и дублирование объектов
Сконфигурируйте новый объект эквалайзера путем клонирования существующего объекта эквалайзера и последующего изменения его свойств. Функции клонирования eqlms чтобы создать независимый эквалайзер, eqcma, затем обновите алгоритм, чтобы 'CMA'.
eqcma = clone(eqlms); eqcma.Algorithm
ans = 'LMS'
eqcma.Algorithm = 'CMA';
eqcma.Algorithmans = 'CMA'
Если вам нужен независимый дубликат, используйте clone команда.
eqlms.NumTaps
ans = 5
eq2 = eqlms; eq2.NumTaps = 6; eq2.NumTaps
ans = 6
eqlms.NumTaps
ans = 6
The clone команда создает копию eqlms который не зависит от eqlms. Напротив, команда eqB = eqA создает eqB как ссылка на eqA, так что eqB и eqA всегда имеют одинаковые настройки свойств.
Линейно выравнивайте систему при помощи различных схем обучения
Линейно выравнивайте символы при помощи обучения на основе EVM
Линейно выравнивайте систему при помощи различных схем обучения
Продемонстрировать линейную эквализацию с помощью алгоритма наименьших средних квадратов (LMS), чтобы восстановить символы QPSK, прошедшие через канал AWGN. Примените различные схемы обучения эквалайзера и отобразите величину ошибки символа.
Setup системы
Симулируйте систему с QPSK-модуляцией, удовлетворяющую AWGN. Передайте пакеты, состоящие из 200 обучающих символов и 1800 случайных символов данных. Сконфигурируйте линейный эквалайзер LMS, чтобы восстановить пакетные данные.
M = 4; numTrainSymbols = 200; numDataSymbols = 1800; SNR = 20; trainingSymbols = pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4); numPkts = 10; lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',5,'ReferenceTap',3,'StepSize',0.01);
Обучите эквалайзер в начале каждого пакета с сбросом
Используйте предварительно обработанные обучающие символы при обработке каждого пакета. После обработки каждого пакета сбросьте эквалайзер. Этот сброс заставляет эквалайзер обучать отводы без предыдущего знания. Сигнал ошибки эквалайзера, графиков для первого, второго и последнего пакета, показывает более высокие символьные ошибки в начале каждого пакета.
jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; rx = awgn(packet,SNR); [~,err] = lineq(rx,trainingSymbols); reset(lineq) if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) title(['Packet # ',num2str(ii)]) xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on; jj = jj+1; end end

Обучите эквалайзер в начале каждого пакета без сброса
Обработайте каждый пакет с помощью предварительно настроенных обучающих символов. Не сбрасывайте эквалайзер после обработки каждого пакета. Не сбрасывая после каждого пакета, эквалайзер сохраняет веса отводов от обучающих предыдущих пакетов. Сигнал ошибки эквалайзера, графиков для первого, второго и последнего пакета, показывает, что после начального обучения на первом пакете последующие пакеты имеют меньше символьных ошибок в начале каждого пакета.
release(lineq) jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; channel = 1; rx = awgn(packet*channel,SNR); [~,err] = lineq(rx,trainingSymbols); if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) title(['Packet # ',num2str(ii)]) xlabel('Symbols') ylabel('Error Magnitude') axis([0,length(packet),0,1]) grid on; jj = jj+1; end end

Периодическое обучение эквалайзера
Системы с сигналами, подверженными изменяющимся во времени каналам, требуют периодического обучения эквалайзера для поддержания блокировки изменений канала. Задайте систему, которая имеет 200 символов обучения на каждые 1800 символов данных. Между обучением эквалайзер не обновляет веса касаний. Эквалайзер обрабатывает 200 символов на пакет.
Rs = 1e6;
fd = 20;
spp = 200; % Symbols per packet
b = randi([0 M-1],numDataSymbols,1);
dataSym = pskmod(b,M,pi/4);
packet = [trainingSymbols; dataSym];
stream = repmat(packet,10,1);
tx = (0:length(stream)-1)'/Rs;
channel = exp(1i*2*pi*fd*tx);
rx = awgn(stream.*channel,SNR);Установите AdaptAfterTraining свойство к false для остановки обновления веса отвода эквалайзера после фазы обучения.
release(lineq) lineq.AdaptAfterTraining = false
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'LMS'
NumTaps: 5
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: false
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
Выравнивание нарушенных данных. Постройте график угловой ошибки из канала, сигнала ошибки эквалайзера и сигнального созвездия. Когда канал изменяется, выход эквалайзера не удаляет эффекты канала. Созвездие выхода вращается вне синхронизации, что приводит к битовым ошибкам.
[y,err] = lineq(rx,trainingSymbols); figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('Time (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(err)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel Without Retraining')

scatterplot(y)

Установите TrainingInputPort свойство к true чтобы сконфигурировать эквалайзер, чтобы переобучить отводы при сигнализации trainFlag вход. Эквалайзер тренируется только тогда, когда trainFlag является true. После каждого 2000 символов эквалайзер переобучает отводы и сохраняет блокировку изменений канала. Постройте график угловой ошибки из канала, сигнала ошибки эквалайзера и сигнального созвездия. Когда канал изменяется, выход эквалайзера удаляет эффекты канала. Выходное созвездие не вращается вне синхронизации, и битовые ошибки уменьшаются.
release(lineq) lineq.TrainingFlagInputPort = true; symbolCnt = 0; numPackets = length(rx)/spp; trainFlag = true; trainingPeriod = 2000; eVec = zeros(size(rx)); yVec = zeros(size(rx)); for p=1:numPackets [yVec((p-1)*spp+1:p*spp,1),eVec((p-1)*spp+1:p*spp,1)] = ... lineq(rx((p-1)*spp+1:p*spp,1),trainingSymbols,trainFlag); symbolCnt = symbolCnt + spp; if symbolCnt >= trainingPeriod trainFlag = true; symbolCnt = 0; else trainFlag = false; end end figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('t (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(eVec)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel With Retraining')

scatterplot(yVec)

Линейно выравнивайте символы при помощи обучения на основе EVM
Восстановите символы QPSK с помощью линейного эквалайзера с помощью обучения ответвлений на основе постоянных модулей (CMA) и EVM. При использовании алгоритмов слепого эквалайзера, таких как CMA, обучите отводы эквалайзера при помощи AdaptWeights свойство для запуска и остановки обучения. Функции Helper используются для генерации графиков и применения фазы коррекции.
Инициализируйте системные переменные.
rng(123456); M = 4; % QPSK numSymbols = 100; numPackets = 5000; raylChan = comm.RayleighChannel('PathDelays',[0 1], ... 'AveragePathGains',[0 -12],'MaximumDopplerShift',1e-5); SNR = 50; adaptWeights = true;
Создайте объекты equalizer и EVM System. Системный объект задает линейный эквалайзер при помощи адаптивного алгоритма CMA. Вызовите функцию helper, чтобы инициализировать графики рисунков.
lineq = comm.LinearEqualizer('Algorithm','CMA', ... 'NumTaps',5,'ReferenceTap',3, ... 'StepSize',0.03,'AdaptWeightsSource','Input port')
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'CMA'
NumTaps: 5
StepSize: 0.0300
Constellation: [1x4 double]
ReferenceTap: 3
InputSamplesPerSymbol: 1
AdaptWeightsSource: 'Input port'
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
info(lineq)
ans = struct with fields:
Latency: 2
evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation'); [errPlot,evmPlot,scatSym,adaptState] = initFigures(numPackets,lineq);
Эквализация Цикла
Для реализации цикла эквализации:
Сгенерируйте пакеты данных PSK.
Примените Релеевское замирание и AWGN к данным передачи.
Примените эквализацию к полученным данным и фазе коррекцию к выходу эквалайзера.
Оцените EVM и переключите adaptWeights флаг в true или false на основе уровня EVM.
Обновите графики рисунков.
for p=1:numPackets data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); rx = awgn(raylChan(tx),SNR); rxDelay = finddelay(rx,tx); [y,err,wts] = lineq(rx,adaptWeights); y = phaseCorrection(y); evmEst = evm(y); adaptWeights = (evmEst > 20); updateFigures(errPlot,evmPlot,scatSym,adaptState, ... wts,y(end),evmEst,adaptWeights,p,numPackets) end

rxDelay
rxDelay = 0
Графики рисунка показывают, что, когда EVM изменяется, эквалайзер переключается и выходит из направленного на принятие решения режима адаптации веса.
Вспомогательные функции
Эта вспомогательная функция инициализирует рисунки, которые показывают квадратичный график результатов симуляции.
function [errPlot,evmPlot,scatter,adaptState] = initFigures(numPkts,lineq) yVec = nan(numPkts,1); evmVec = nan(numPkts,1); wVec = zeros(lineq.NumTaps,1); adaptVec = nan(numPkts,1); figure subplot(2,2,1) evmPlot = stem(wVec); grid on; axis([1 lineq.NumTaps 0 1.8]) xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2) scatter = plot(yVec, '.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on xlabel('In-phase'); ylabel('Quadrature'); title('Scatter Plot'); subplot(2,2,3) adaptState = plot(adaptVec); grid on; axis([0 numPkts -0.2 1.2]) ylabel('Training'); xlabel('Symbols'); title('Adapt Weights Signal') subplot(2,2,4) errPlot = plot(evmVec); grid on; axis([1 numPkts 0 100]) xlabel('Symbols'); ylabel('EVM (%)'); title('EVM') end
Эта вспомогательная функция обновляет рисунки.
function updateFigures(errPlot,evmPlot,scatSym, ... adaptState,w,y,evmEst,adaptWts,p,numFrames) persistent yVec evmVec adaptVec if p == 1 yVec = nan(numFrames,1); evmVec = nan(numFrames,1); adaptVec = nan(numFrames,1); end yVec(p) = y; evmVec(p) = evmEst; adaptVec(p) = adaptWts; errPlot.YData = abs(evmVec); evmPlot.YData = abs(w); scatSym.XData = real(yVec); scatSym.YData = imag(yVec); adaptState.YData = adaptVec; drawnow limitrate end
Эта вспомогательная функция применяет коррекцию фазы.
function y = phaseCorrection(y) a = angle(y((real(y) > 0) & (imag(y) > 0))); a(a < 0.1) = a(a < 0.1) + pi/2; theta = mean(a) - pi/4; y = y * exp(-1i*theta); end
Для правильной эквализации необходимо определить и учесть задержки системы. Как показано в следующем примере, можно использовать finddelay функция для определения системной задержки. Этот пример использует линейную эквализацию LMS, но тот же подход действителен для адаптивных алгоритмов RLS и CMA и для эквалайзеров обратной связи принятия решений.
Линейно выравнивание задержанного сигнала
Симулируйте систему с задержкой между переданными символами и принятыми выборками. Типичные системы имеют фильтры передатчика и приемника, которые приводят к задержке. Эта задержка должна быть учтена для синхронизации системы. В этом примере системная задержка вводится без фильтров передачи и приема. Линейная эквализация, используя алгоритм наименьших средних квадратов (LMS), восстанавливает символы QPSK.
Инициализируйте переменные симуляции.
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
mpChan = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];
systemDelay = dsp.Delay(20);
snr = 24;Сгенерируйте модулированные QPSK символы. Примените многолучевую фильтрацию канала, системную задержку и AWGN к переданным символам.
data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); % OQPSK delayedSym = systemDelay(filter(mpChan,1,tx)); rx = awgn(delayedSym,snr,'measured');
Создайте объекты equalizer и EVM System. Системный объект задает линейный эквалайзер, который использует LMS-алгоритм.
lineq = comm.LinearEqualizer('Algorithm','LMS', ... 'NumTaps',9,'ReferenceTap',5); evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation');
Выравнивание без корректировки входной задержки
Выравнивание полученных символов.
[y1,err1,wts1] = lineq(rx,tx(1:numTrainingSymbols,1));
Найдите задержку между принятыми символами и переданными символами с помощью finddelay функция.
rxDelay = finddelay(tx,rx)
rxDelay = 20
Отображение информации об эквалайзере. Значение задержки указывает задержку, введенную эквалайзером. Вычислим общую задержку как сумму rxDelay и задержку эквалайзера.
eqInfo = info(lineq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency;
Пока выход эквалайзера не сходится, вероятность ошибки символа высока. Постройте график выхода ошибки, err1, чтобы определить, когда выровненный выход сходится.
plot(abs(err1)) xlabel('Symbols') ylabel('Error Magnitude') title('Equalizer Error Signal')

График показывает чрезмерные ошибки после периода обучения 1000 символов. При демодуляции символов и вычислении ошибок символов, для расчета безсовпадающего вывода и системной задержки между выходом эквалайзера и переданными символами, пропустите первые 2000 символов.
dataRec1 = pskdemod(y1(2000+totalDelay:end),M,pi/4); symErrWithDelay = symerr(data(2000:end-totalDelay),dataRec1)
symErrWithDelay = 5999
evmWithDelay = evm(y1)
evmWithDelay = 29.5795
Вероятность ошибок и EVM высоки, потому что задержка приема не была учтена в Системный объект эквалайзера.
Настройте входную задержку в эквалайзере
Выравнивание полученных данных при помощи значения задержки для установки InputDelay свойство. Потому что InputDelay является свойством nontunable, вы должны освободить lineq Системный объект для перенастройки InputDelay свойство. Выравнивание полученных символов.
release(lineq) lineq.InputDelay = rxDelay
lineq =
comm.LinearEqualizer with properties:
Algorithm: 'LMS'
NumTaps: 9
StepSize: 0.0100
Constellation: [1x4 double]
ReferenceTap: 5
InputDelay: 20
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
[y2,err2,wts2] = lineq(rx,tx(1:numTrainingSymbols,1));
Постройте график весов отвода и выровненной величины ошибки. A диаграммы лист-ствол показывает веса отводов эквалайзера до и после удаления системной задержки. A 2D графика показывает более медленное сходимость эквалайзера для задержанного сигнала по сравнению с сигналом с удаленной задержкой.
subplot(2,1,1) stem([real(wts1),real(wts2)]) xlabel('Taps') ylabel('Tap Weight Real') legend('rxDelayed','rxDelayRemoved') grid on subplot(2,1,2) stem([imag(wts1),imag(wts2)]) xlabel('Taps') ylabel('Tap Weight Imaginary') legend('rxDelayed','rxDelayRemoved') grid on

figure plot([abs(err1),abs(err2)]) xlabel('Symbols') ylabel('Error Magnitude') legend('rxDelayed','rxDelayRemoved') grid on

Постройте выход ошибок уравненных сигналов, rxDelayed и rxDelayRemoved. Для сигнала, который имеет удаленную задержку, эквалайзер сходится в течение периода обучения 1000 символов. При демодуляции символов и вычислении ошибок символов, для расчета безсовпадающего вывода и системной задержки между выходом эквалайзера и переданными символами, пропустите первые 500 символов. Перенастройка эквалайзера с учетом задержки системы позволяет лучше выравнивать сигнал и уменьшает ошибки символов и EVM.
eqInfo = info(lineq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency; dataRec2 = pskdemod(y2(500+totalDelay:end),M,pi/4); symErrDelayRemoved = symerr(data(500:end-totalDelay),dataRec2)
symErrDelayRemoved = 0
evmDelayRemoved = evm(y2(500+totalDelay:end))
evmDelayRemoved = 9.4435
Эта модель показывает поведение выбранного адаптивного эквалайзера в ссылке связи, который имеет канал с замираниями. Передатчик и приемник имеют корневую повышенную косинусоидальную импульсную фильтрацию. Блок подсистемы позволяет вам выбрать между линейными или решающими эквалайзерами с обратной связью, которые используют адаптивный алгоритм наименьшего среднего квадрата (LMS) или рекурсивного наименьшего квадрата (RLS).
Структура модели
Передатчик генерирует 16QAM данные случайных сигналов, которые включают в себя обучающую последовательность и применяет корневую приподнятой косинусоидальной импульсной фильтрации.
Нарушения канала включают многолучевое замирание, Допплеровский сдвиг, смещение несущей частоты, переменную целочисленную задержку, потери при распространении в свободном пространстве и AWGN.
Приемник применяет корневую приподнятую косинусоидальную импульсную фильтрацию, настраивает коэффициент усиления, включает управление режимом эквалайзера, чтобы включить обучение и позволяет вам выбрать алгоритм эквалайзера из этих вариантов.

Возможности помогают вам понять, как ведут себя различные эквалайзеры и адаптивные алгоритмы.
Исследуйте модель примера

Эксперименты с моделью
Эта модель предоставляет несколько способов для вас, чтобы изменить настройки и наблюдать результаты. The InitFcn найдено в File>Model Properties>Callbacks вызывает cm_ex_adaptive_eq_with_fading_init для инициализации модели. Этот файл позволяет вам варьировать настройки в модели, включая:
Системные параметры, такие как ОСШ.
Параметры фильтра формирования импульсов, такие как сгиб и длина фильтра
Значение потерь пути.
Условия канала: Релей или Райс с замираниями, увеличение пути канала, задержки пути канала и Допплеровский сдвиг.
Выбор и строение эквалайзера.
Модельные факторы
Эта нестандартная ссылка связи является репрезентативной для современной коммуникационной системы.
Оптимальное строение эквалайзера зависит от условий канала. Файл инициализации устанавливает параметры Doppler shift и многолучевой канал с замираниями, которые подчеркивают возможности различных эквалайзеров.

Структура эквалайзера с обратной связью принятия решения работает лучше, чем структура линейного эквалайзера для более высокой межсимвольной интерференции.
Алгоритм RLS работает лучше, чем LMS-алгоритм для более высоких доплеровских частот.
LMS-алгоритм выполняется быстро, сходится медленно, и его сложность увеличивается линейно с количеством весов.
Алгоритм RLS сходится быстро, его сложность увеличивается приблизительно как квадрат числа весов. Он может быть нестабильным, когда количество весов большое.
Каналы, выполняемые для различных эквалайзеров, имеют следующие характеристики.

Начальные настройки для других ослаблений канала одинаковы для всех эквалайзеров. Значение смещения несущей частоты устанавливается равным 50 Гц. Потери при распространении в свободном пространстве устанавливаются на 60 дБ. Переменная целочисленная задержка устанавливается в 2 выборки, что требует, чтобы эквалайзеры выполнили некоторое восстановление синхронизации.
Глубокие затухания канала и потери пути могут привести к тому, что уровень входного сигнала эквалайзера будет намного меньше необходимого уровня выходного сигнала и привести к недопустимо длительному времени сходимости эквалайзера. The AGC блок регулирует величину принимаемого сигнала, чтобы уменьшить время сходимости эквалайзера. Необходимо настроить оптимальный уровень выходной степени усиления на основе выбранной схемы модуляции. Для 16QAM используется желаемая выходная степень 10 Вт.
Обучение эквалайзера выполняется в начале симуляции.
Выполнение симуляции
Выполнение симуляции вычисляет статистику ошибок символов и создает следующие рисунки:
Сигнальное созвездие после приёмного фильтра.
Сигнальное созвездие после регулировки усиления.
Показана сигнальная сигнальная сигнализация после эквализации с измерениями качества сигнала.
График ошибки эквалайзера.
Для графиков, показанных здесь, выбран алгоритм эквалайзера RLS Linear. Отслеживая эти рисунки, можно увидеть, что качество принимаемого сигнала колеблется по мере развития времени симуляции.
На графиках созвездий After Rx и After AGC показан сигнал перед эквализацией. После AGC показывает влияние условий канала на переданный сигнал. График After Eq показывает сигнал после эквализации. Сигнал, нанесенный на диаграмму созвездия после эквализации, показывает изменение качества сигнала, основанное на эффективности процесса эквализации. На протяжении всей симуляции сигнальные созвездия, построенные до эквализации, заметно отклоняются от 16QAM сигнального созвездия. Созвездие After Eq улучшается или ухудшается, когда изменяется сигнал ошибки эквалайзера. The Eq error нанесенный на график ошибки Eq, указывает на плохую эквализацию в начале симуляции. Ошибка сначала ухудшается, затем улучшается, когда эквалайзер сходится.




Дальнейшие исследования
Дважды кликните Equalizer Selector блокируйте и выберите другой эквалайзер. Запустите симуляцию, чтобы увидеть эффективность различных опций эквалайзера. Можно использовать регистратор сигналов, чтобы сравнить результаты этого эксперимента. На блоке щелкните правой кнопкой мыши по сигнальным проводам и выберите Log Selected Signals. Если вы активировали логгирование сигналов, после концов запуска симуляции откройте Данные Моделирования Inspector, чтобы просмотреть записанные сигналы.
В командной строке MATLAB™ введите edit cm_ex_adaptive_eq_with_fading_init.m чтобы открыть файл инициализации, измените параметр и перезапустите симуляцию. Для примера отрегулируйте характеристики канала (params.maxDoppler|, params.pathDelays, и params.pathGains). Адаптивный алгоритм RLS работает лучше, чем адаптивный алгоритм LMS, поскольку максимальный Доплер увеличивается.