Этот пример показывает, как создать произвольный блок путем соединения моделей с помощью connect. Система является предиктором Смита, системой управления с одним входом, одним выходом (SISO) и несколькими циклами, показанными на следующем блоке.
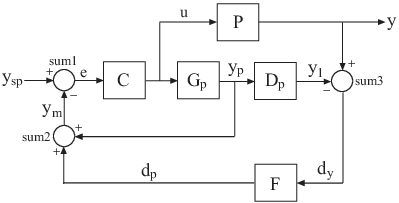
Для получения дополнительной информации о предикторе Смита, см. Управление процессами с длинным мертвым временем: Предсказатель Смита.
connect Команда позволяет вам создать общую передаточную функцию от ysp до y. Как использовать connect, задайте имена входного и выходного каналов компонентов блока. connect автоматически соединяет порты с таким же именем, как показано на следующем рисунке.

Чтобы создать модель замкнутого цикла системы Smith Predictor от ysp до y:
Создайте компоненты блока: модель процесса P, модель предиктора Gp, модель задержки Dp, фильтр Fи ПИ-контроллер C. Задайте имена для входа и выходных каналов каждой модели так, чтобы connect может автоматически присоединиться к ним, чтобы создать блок.
s = tf('s');
P = exp(-93.9*s) * 5.6/(40.2*s+1);
P.InputName = 'u'; P.OutputName = 'y';
Gp = 5.6/(40.2*s+1);
Gp.InputName = 'u'; Gp.OutputName = 'yp';
Dp = exp(-93.9*s);
Dp.InputName = 'yp'; Dp.OutputName = 'y1';
F = 1/(20*s+1);
F.InputName = 'dy'; F.OutputName = 'dp';
C = pidstd(0.574,40.1);
C.Inputname = 'e'; C.OutputName = 'u';Создайте суммирующие соединения, необходимые для выполнения блока.
sum1 = sumblk('e = ysp - ym');
sum2 = sumblk('ym = yp + dp');
sum3 = sumblk('dy = y - y1');Аргумент в: sumblk является формулой, которая связывает входной и выходной сигналы суммирующего соединения. sumblk создает суммирующее соединение с именами входного и выходного сигналов, заданными в формуле. Для примера, в sum1, формула 'e = ysp - ym' задает сигнал выхода с именем e, что является различием между входными сигналами с именем ysp и ym.
Собрать полную модель от ysp до y.
T = connect(P,Gp,Dp,C,F,sum1,sum2,sum3,'ysp','y');
Вы можете перечислить модели и суммирующие соединения в любом порядке, потому что connect автоматически соединяет их, используя имена входного и выходного каналов.
Последние два аргумента определяют входной и выходной сигналы многоканальной структуры управления. Таким образом, T является ss модель с входными ysp и выход y.