Правила LQG: Пример прокатного стана

Обзор этого тематического исследования

Этот пример демонстрирует использование инструментов проекта LQG в приложении управления процессами. Цель состоит в том, чтобы регулировать горизонтальную и вертикальную толщину балки, произведенной станом горячей прокатки. Этот пример адаптирован к [1]. Полная модель объекта управления является MIMO, и пример показывает преимущество прямой разработки MIMO LQG по сравнению с отдельными проектами SISO для каждой оси. Напечатать

milldemo

в командной строке, чтобы запустить эту демонстрацию в интерактивном режиме.

Модели процесса и возмущения

Прокатный стан предназначен для формирования прямоугольных балок из горячего металла. Требуемая исходящая форма нарисована ниже.

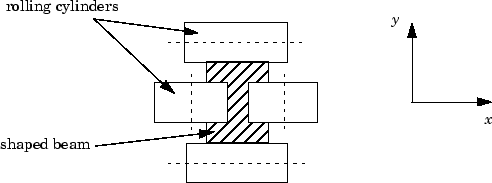
Эта форма впечатлена двумя парами цилиндров качения (по одной на ось), расположенных гидравлическими приводами. Зазор между двумя цилиндрами называется зазором крена.

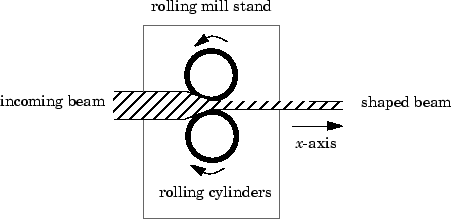
Цель состоит в том, чтобы сохранить толщину балки вдоль x- и y- осей в пределах допусков обеспечения качества. Изменения выхода толщины могут возникнуть из-за следующего:

Изменения толщины/твердости входящей балки
Эксцентриситет в цилиндрах качения

Управление с обратной связью необходимо, чтобы уменьшить эффект этих нарушений порядка. Поскольку зазор крена не может быть измерен близко к стану мельницы, вместо этого для обратной связи используется сила качения.

Толщина входа нарушения порядка моделируется как фильтр нижних частот, управляемый белым шумом. Нарушение порядка эксцентриситета является приблизительно периодическим, и его частота является функцией скорости качения. Разумной моделью для этого нарушения порядка является полосно-пропускающий фильтр второго порядка, управляемый белым шумом.

Это приводит к следующей типовой модели для каждой оси процесса качения.

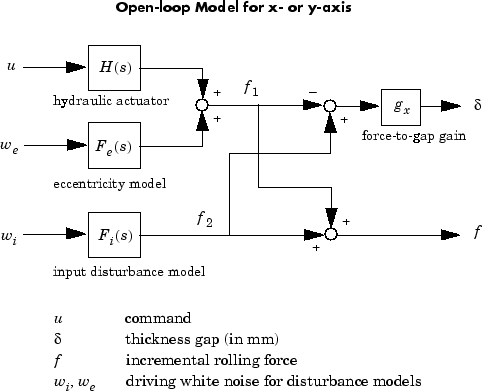
Измеренное f изменения силы качения является комбинацией добавочной силы, приложенной гидравлическим приводом, и нарушений порядка, обусловленных эксцентриситетом и изменением входной толщины. Обратите внимание, что:

Выходы H (s), _Fe (s) и Fi (s) являются инкрементными силами, доставляемыми каждым компонентом.
Увеличение гидравлической силы или силы эксцентриситета уменьшает выход δ зазора толщины.
Увеличение толщины входа увеличивает этот зазор.

Данные модели для каждой оси обобщены ниже.

Моделируйте данные для оси X

$\begin{array}{l} H_{x} (s) = \frac{2.4 \times 10^{8}}{s^{2} + 72 s + 90^{2}} \\ F_{i x} (s) = \frac{10^{4}}{s + 0.05} \\ F_{e x} (s) = \frac{3 \times 10^{4} s}{s^{2} + 0.125 s + 6^{2}} \\ g_{x} = 10^{- 6} \end{array}$

Данные модели для оси Y

$\begin{array}{l} H_{y} (s) = \frac{7.8 \times 10^{8}}{s^{2} + 71 s + 88^{2}} \\ F_{i y} (s) = \frac{2 \times 10^{4}}{s + 0.05} \\ F_{e y} (s) = \frac{10^{5} s}{s^{2} + 0.19 s + {9.4}^{2}} \\ g_{y} = 0.5 \times 10^{- 6} \end{array}$

Проект LQG для оси X

В качестве первого приближения игнорируйте поперечное сцепление между x - и y - осями и обрабатывайте каждую ось независимо. То есть спроектируйте по одному регулятору SISO LQG для каждой оси. Цель проекта состоит в том, чтобы уменьшить изменения толщины δx и δy из-за эксцентриситета и нарушений порядка толщины.

Начните с x оси. Сначала задайте компоненты модели как объекты передаточной функции.

% Hydraulic actuator (with input "u-x")
Hx = tf(2.4e8,[1 72 90^2],'inputname','u-x')

% Input thickness/hardness disturbance model
Fix = tf(1e4,[1 0.05],'inputn','w-ix')

% Rolling eccentricity model
Fex = tf([3e4 0],[1 0.125 6^2],'inputn','w-ex')

% Gain from force to thickness gap
gx = 1e-6;

Затем создайте модель разомкнутого контура, показанную в моделях процесса и возмущения. Можно использовать функцию connect с этой целью, но проще создать эту модель элементарными append и series соединения.

% I/O map from inputs to forces f1 and f2
Px = append([ss(Hx) Fex],Fix)

% Add static gain from f1,f2 to outputs "x-gap" and "x-force" 
Px = [-gx gx;1 1] * Px

% Give names to the outputs:
set(Px,'outputn',{'x-gap' 'x-force'})

Примечание

Чтобы получить минимальные реализации пространства состояний, всегда преобразуйте модели передаточной функции в пространство состояний перед их соединением. Объединение передаточных функций и затем преобразование в пространство состояний может привести к неминимальным моделям пространства состояний.

Переменная Px теперь содержит модель пространства состояний без разомкнутого контура с входными и выходными именами.

Px.inputname

ans = 
    'u-x'
    'w-ex'
    'w-ix'

Px.outputname

ans = 
    'x-gap'
    'x-force'

Второй выходной 'x-force' - измерение силы качения. Регулятор LQG будет использовать это измерение, чтобы привести в действие гидравлический привод и уменьшить _δx изменения толщины, вызванные возмущениями.

Проект LQG включает два шага:

Разработайте коэффициент усиления с полной обратной связью, который минимизирует показатель эффективности LQ вида
$J (u_{x}) = \int_{0}^{\infty} {q δ_{x}^{2} + r u_{x}^{2}} d t$
Спроектируйте фильтр Калмана, который оценивает вектор состояния, учитывая измерения силы 'x-force'.

Критерий эффективности J (_ux) одинаково наказывает низкие и высокие частоты. Поскольку низкочастотные изменения имеют первостепенное значение, устраните высокочастотное содержимое _δx с низкочастотным фильтром 30/( s + 30) и используйте отфильтрованное значение в критерии эффективности LQ.

lpf = tf(30,[1 30])

% Connect low-pass filter to first output of Px
Pxdes = append(lpf,1) * Px
set(Pxdes,'outputn',{'x-gap*' 'x-force'})

% Design the state-feedback gain using LQRY and q=1, r=1e-4
kx = lqry(Pxdes(1,1),1,1e-4)

Примечание

lqry ожидает, что все входы будут командами, а все выходы измерениями. Здесь команда 'u-x' и измерение 'x-gap*' (отфильтрованная погрешность) являются первым входом и первым выходом Pxdes. Поэтому используйте синтаксис Pxdes(1,1) чтобы задать только отношение ввода-вывода между 'u-x' и 'x-gap*'.

Затем спроектируйте Оценку состояния фильтра Калмана с помощью функции kalman. Технологический шум

$w_{x} = [\begin{array}{l} w_{e x} \\ w_{i x} \end{array}]$

имеет единичную ковариацию по конструкции. Установите ковариацию шума измерения равную 1000, чтобы ограничить коэффициент усиления высокой частоты и сохранить только измеренный выход 'x-force' для проекта оценщика.

estx = kalman(Pxdes(2,:),eye(2),1000)

Наконец, соедините усиление обратной связи о состоянии kx и устройство оценки состояния estx для формирования регулятора LQG.

Regx = lqgreg(estx,kx)

Это завершает проект LQG для оси x −.

Рассмотрим ответ регулятора Bode от 0,1 до 1000 рад/сек.

h = bodeplot(Regx,{0.1 1000})
setoptions(h,'PhaseMatching','on')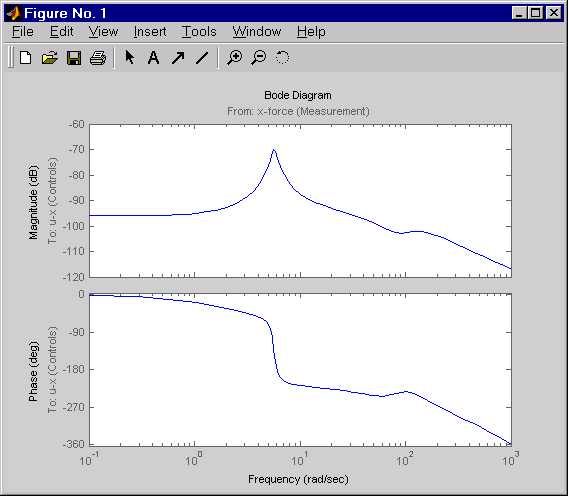

Фазовый отклик имеет интересную физическую интерпретацию. Сначала рассмотрим увеличение толщины входа. Это низкочастотное нарушение порядка увеличивает как толщину выхода так и силу качения. Потому что фаза регулятора составляет приблизительно 0^o на низких частотах цикл обратной связи затем адекватно реагирует путем увеличения гидравлической силы для смещения увеличения толщины. Теперь рассмотрим эффект эксцентриситета. Эксцентриситет вызывает колебания зазора крена (зазор между цилиндрами качения). Когда зазор крена минимален, сила качения увеличивается, и толщина балки уменьшается. Затем гидравлическая сила должна быть уменьшена (обратная связь отрицательной силы), чтобы восстановить требуемую толщину. Именно это и делает регулятор LQG, когда его фаза падает до -180^o около естественной частоты нарушения порядка эксцентриситета (6 рад/сек).

Затем сравните отклики разомкнутого и замкнутого контуров от нарушения порядка до зазора толщины. Использование feedback чтобы закрыть цикл. Чтобы помочь задать подключение обратной связи, проверьте имена ввода-вывода объекта Px и регулятор Regx.

Px.inputname
ans = 
    'u-x'
    'w-ex'
    'w-ix'
 
Regx.outputname
ans = 
    'u-x'
 
Px.outputname
ans = 
    'x-gap'
    'x-force'
 
Regx.inputname
ans = 
    'x-force'

Это указывает, что вы должны подключить первый вход и второй выход Px регулятору.

clx = feedback(Px,Regx,1,2,+1)       % Note: +1 for positive feedback

Теперь вы готовы сравнить отклики Bode в разомкнутом и замкнутом контурах от нарушения порядка до зазора толщины.

h = bodeplot(Px(1,2:3),'--',clx(1,2:3),'-',{0.1 100})
setoptions(h,'PhaseMatching','on')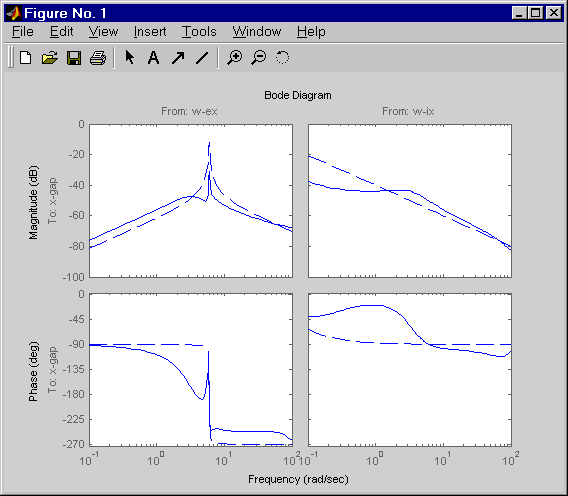

Штриховые линии показывают разомкнутому контуру ответ. Обратите внимание, что пиковое усиление отклика эксцентриситет-зазор и низкочастотное усиление отклика входа-толщина-зазор были уменьшены примерно на 20 дБ.

Наконец, используйте lsim для симуляции временных характеристик разомкнутого и замкнутого контуров на входы белого шума _wex и _wix. Выберите dt=0.01 в качестве шага расчета для симуляции и вывода эквивалентных дискретных входных входов белого шума для этой частоты дискретизации.

dt = 0.01
t = 0:dt:50   % time samples

% Generate unit-covariance driving noise wx = [w-ex;w-ix].
% Equivalent discrete covariance is 1/dt
wx = sqrt(1/dt) * randn(2,length(t))

lsim(Px(1,2:3),':',clx(1,2:3),'-',wx,t)

Щелкните правой кнопкой мыши на появившемся графике и выберите Show Input, чтобы выключить отображение входа.

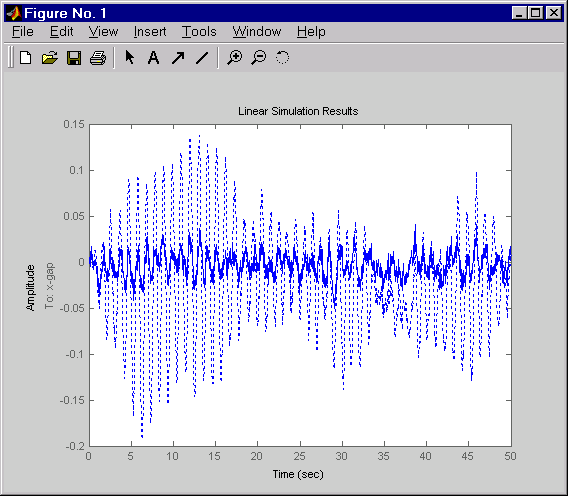
Пунктирные линии соответствуют разомкнутому контуру отклику. В этой симуляции регулирование LQG уменьшает изменение пиковой толщины на 4 множителя.

Проект LQG для оси Y

Проект LQG для оси y (регулирование толщины y) выполняется точно так же, как и для оси x.

% Specify model components
Hy = tf(7.8e8,[1 71 88^2],'inputn','u-y') 
Fiy = tf(2e4,[1 0.05],'inputn','w-iy') 
Fey = tf([1e5 0],[1 0.19 9.4^2],'inputn','w-ey')
gy = 0.5e-6 % force-to-gap gain

% Build open-loop model
Py = append([ss(Hy) Fey],Fiy)
Py = [-gy gy;1 1] * Py
set(Py,'outputn',{'y-gap' 'y-force'})

% State-feedback gain design
Pydes = append(lpf,1) * Py % Add low-freq. weigthing
set(Pydes,'outputn',{'y-gap*' 'y-force'})
ky = lqry(Pydes(1,1),1,1e-4)

% Kalman estimator design
esty = kalman(Pydes(2,:),eye(2),1e3)

% Form SISO LQG regulator for y-axis and close the loop
Regy = lqgreg(esty,ky)
cly = feedback(Py,Regy,1,2,+1)

Сравните ответ открытия и замкнутого контура с входными нарушениями порядка белого шума.

dt = 0.01
t = 0:dt:50
wy = sqrt(1/dt) * randn(2,length(t))

lsim(Py(1,2:3),':',cly(1,2:3),'-',wy,t)

Щелкните правой кнопкой мыши на появившемся графике и выберите Show Input, чтобы выключить отображение входа.

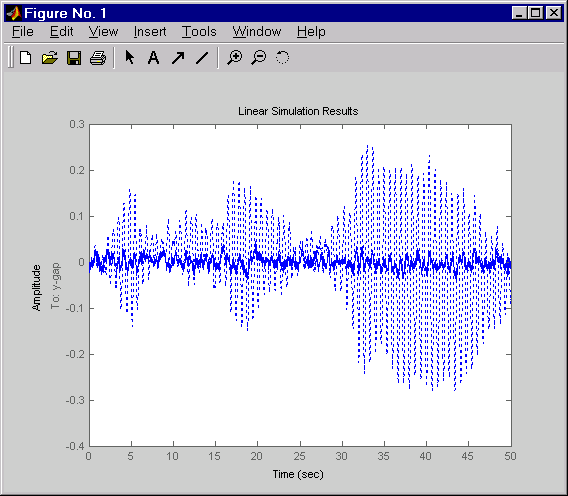
Пунктирные линии соответствуют разомкнутому контуру отклику. Результаты моделирования сопоставимы с результатами для оси x -.

Поперечное сцепление между осями

Регулирование толщины x/ y является задачей MIMO. До сих пор вы обрабатывали каждую ось отдельно и закрывали по одному циклу SISO за раз. Этот проект действителен, пока две оси довольно развязаны. К сожалению, этот процесс прокатки показывает некоторую степень поперечного сцепления между осями. Физически увеличение гидравлической силы вдоль оси x сжимает материал, что, в свою очередь, увеличивает силу отталкивания на цилиндрах оси y. Результатом является увеличение y -толщины и эквивалентное (относительное) уменьшение гидравлической силы вдоль оси y.

Рисунок ниже показывает муфту.

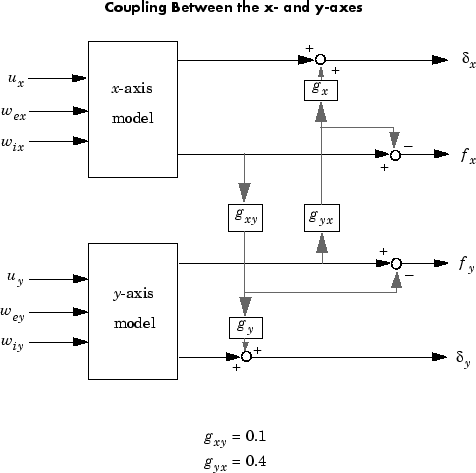
Соответственно, погрешности толщины и силы качения связаны с выходами ${\bar{δ}}_{x}, {\bar{f}}_{x}, \dots$ моделей оси x - и y - по

$[\begin{array}{l} δ_{x} \\ δ_{y} \\ f_{x} \\ f_{x} \end{array}] = \underset{матрица кросс-связок}{\underset{︸}{[\begin{matrix} 1 & 0 & 0 & g_{y x} g_{x} \\ 0 & 1 & g_{x y} g_{y} & 0 \\ 0 & 0 & 1 & - g_{y x} \\ 0 & 0 & - g_{x y} & 1 \end{matrix}]}} [\begin{array}{l} {\bar{δ}}_{x} \\ {\bar{δ}}_{y} \\ {\bar{f}}_{x} \\ {\bar{f}}_{y} \end{array}]$

Посмотрим, как учитывается предыдущий «развязанный» проектный тариф LQG при перекрестном соединении. Чтобы создать модель с двумя осями, показанную выше, добавьте модели Px и Py для x - и y - осей.

P = append(Px,Py)

Для удобства измените порядок входов и выходов так, чтобы команды и погрешности толщины появились первыми.

P = P([1 3 2 4],[1 4 2 3 5 6])
P.outputname

ans = 
    'x-gap'
    'y-gap'
    'x-force'
    'y-force'

Наконец, поместите матрицу поперечных связей последовательно с выходами.

gxy = 0.1; gyx = 0.4;
CCmat = [eye(2) [0 gyx*gx;gxy*gy 0] ; zeros(2) [1 -gyx;-gxy 1]]
Pc = CCmat * P
Pc.outputname = P.outputname

Чтобы симулировать реакцию с обратной связью, также сформируйте модель с обратной связью

feedin = 1:2 % first two inputs of Pc are the commands
feedout = 3:4 % last two outputs of Pc are the measurements
cl = feedback(Pc,append(Regx,Regy),feedin,feedout,+1)

Теперь вы готовы симулировать открыто- и замкнутые реакции на движущие белые шумы wx (для оси x) и wy (для оси y).

wxy = [wx ; wy]
lsim(Pc(1:2,3:6),':',cl(1:2,3:6),'-',wxy,t)

Щелкните правой кнопкой мыши на появившемся графике и выберите Show Input, чтобы выключить отображение входа.

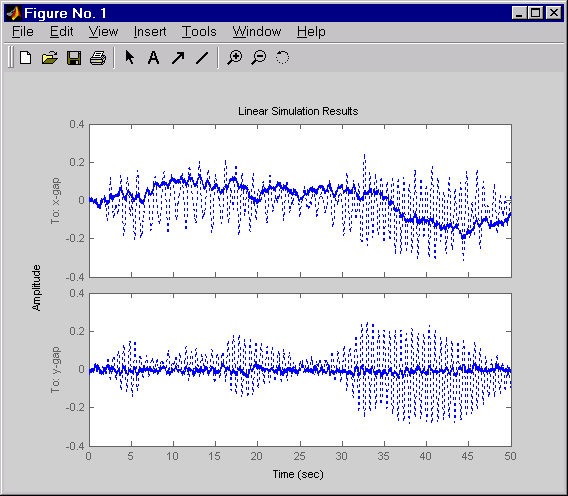
Реакция показывает сильное ухудшение эффективности регулирования вдоль оси x (изменение пиковой толщины примерно в четыре раза больше, чем в симуляции без поперечного сцепления). Следовательно, разработка для одного цикла за раз не подходит для этого уровня сцепления, и вы должны выполнить проект MIMO оси соединения, чтобы правильно обработать эффекты сцепления.

MIMO LQG Проекта

Начните с полной двухосевой модели пространства состояний Pc получен в перекрестном соединении между осями. Эти входы и выходы модели

Pc.inputname

ans = 
    'u-x'
    'u-y'
    'w-ex'
    'w-ix'
    'w_ey'
    'w_iy'

P.outputname

ans = 
    'x-gap'
    'y-gap'
    'x-force'
    'y-force'

Как и ранее, добавьте низкочастотные фильтры последовательно с 'x-gap' и 'y-gap' выходы для штрафования только низкочастотных изменений толщины.

Pdes = append(lpf,lpf,eye(2)) * Pc
Pdes.outputn = Pc.outputn

Далее спроектируйте усиление LQ и оценку состояния как раньше (теперь есть две команды и два измерения).

k = lqry(Pdes(1:2,1:2),eye(2),1e-4*eye(2))      % LQ gain
est = kalman(Pdes(3:4,:),eye(4),1e3*eye(2))     % Kalman estimator

RegMIMO = lqgreg(est,k)      % form MIMO LQG regulator

Получившийся регулятор LQG RegMIMO имеет два входа и два выхода.

RegMIMO.inputname

ans = 
    'x-force'
    'y-force'

RegMIMO.outputname

ans = 
    'u-x'
    'u-y'

Постройте график его сингулярного значения отклика (основные усиления).

sigma(RegMIMO)

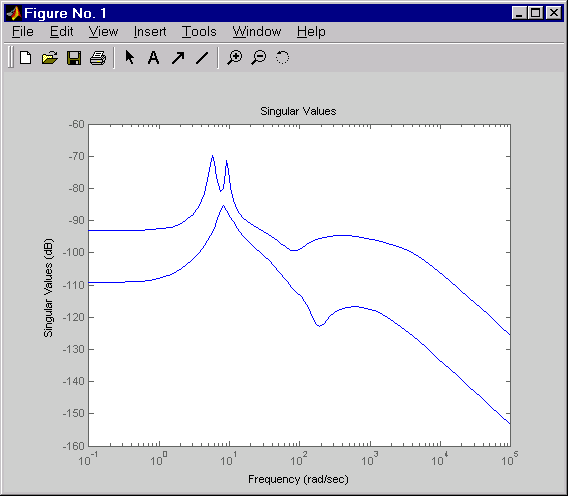
Затем постройте график временных характеристик разомкнутого и замкнутого контуров на входы белого шума (используя для обратной связи регулятор MIMO LQG).

% Form the closed-loop model
cl = feedback(Pc,RegMIMO,1:2,3:4,+1);

% Simulate with lsim using same noise inputs
lsim(Pc(1:2,3:6),':',cl(1:2,3:6),'-',wxy,t)

Щелкните правой кнопкой мыши на появившемся графике и выберите Show Input, чтобы выключить отображение входа.

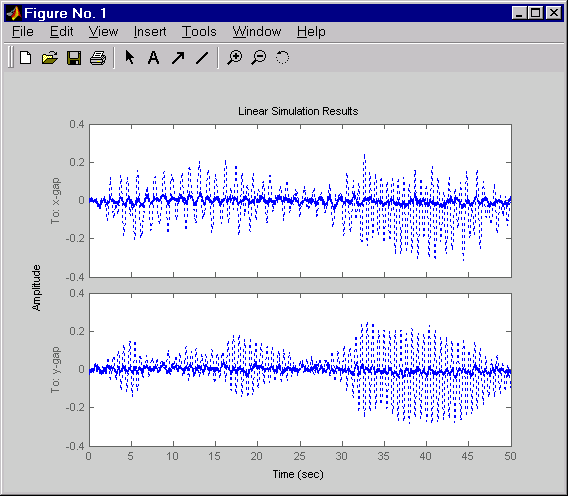
Проект MIMO является явным улучшением по сравнению с отдельными проектами SISO для каждой оси. В частности, уровень изменения толщины x/ y теперь сопоставим с уровнем, полученным в разцепленном случае. Этот пример иллюстрирует преимущества прямого проекта MIMO для многопараметрических систем.

Ссылки

[1] Grimble, M.J., Robust Industrial Control: Optimal Design Approach for Polynomial Systems, Prentice Hall, 1994, p. 261 and pp. 443-456.

Документация