Этот пример подходит для данных ENSO с помощью нескольких пользовательских нелинейных уравнений. Данные ENSO состоят из ежемесячных усреднённых различий атмосферного давления между островом Пасхи и Дарвином, Австралия. Это различие движет пассивными ветрами в южном полушарии.
Данные ENSO явно периодичны, что предполагает, что их можно описать серией Фурье:
где ai и bi являются амплитудами, и ci являются периодами (циклами) данных. Вопрос, на который нужно ответить, сколько циклов существует?
В качестве первой попытки примите один цикл и подгоняйте данные с помощью одного косинуса и одного синуса.
Если подгонка не описывает данные хорошо, добавьте дополнительные условия косинуса и синуса с уникальными коэффициентами периода, пока не будет получена хорошая подгонка.
Уравнение нелинейно, потому что неизвестный коэффициент c 1 включен в состав тригонометрических аргументов функции.
Загрузите данные и откройте приложение Аппроксимирование Кривыми:
load enso cftool
Тулбокс включает ряд Фурье в качестве нелинейного библиотечного уравнения. Однако библиотечное уравнение не удовлетворяет потребностям этого примера, потому что его условия заданы как фиксированные множители основной частотной w. Для получения дополнительной информации см. раздел «Серия Фурье». Создайте встроенную библиотеку Fourier fit, чтобы сравнить с вашими пользовательскими уравнениями:
Выберите month для X data и pressure для Y data.
Выберите Fourier для типа модели.
Введите Fourier для Fit name.
Измените количество терминов на 8.
Наблюдайте за подгонкой модели библиотеки. На следующих шагах вы создадите пользовательские уравнения для сравнения.
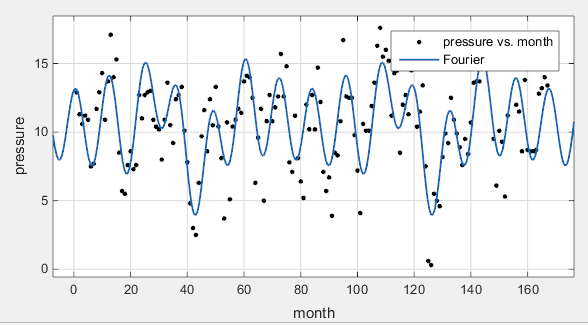
Повторите вашу подгонку. Щелкните правой кнопкой мыши подгонку в Table of Fits и выберите Duplicate ‘Fourier’.
Назовите новую Enso1Period подгонки.
Измените тип модели на Fourier на Custom Equation.
Замените текст примера в поле редактирования уравнения на
a0+a1*cos(2*pi*x/c1)+b1*sin(2*pi*x/c1)
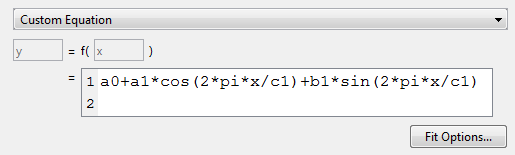
Тулбокс применяет подгонку к enso данные.
Графические и числовые результаты, показанные здесь, показывают, что подгонка не описывает данные хорошо. В частности, подобранное значение для c1 необоснованно мало. Ваши начальные результаты подгонки могут отличаться от этих результатов, потому что начальные точки выбраны случайным образом.
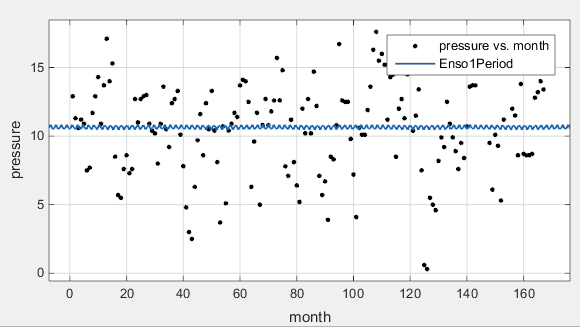

По умолчанию коэффициенты неограниченны и имеют случайные начальные значения от 0 до 1. Данные включают периодический компонент с периодом около 12 месяцев. Однако с c1 без ограничений и со случайной начальной точкой эта подгонка не смогла найти этот цикл.
Чтобы помочь процедуре аппроксимации, ограничьте c1 к значению от 10 до 14. Нажмите кнопку Fit Options, чтобы просмотреть и изменить ограничения для неизвестных коэффициентов.
В диалоговом окне Опции обратите внимание, что по умолчанию коэффициенты неограниченны (границы -Inf и Inf).
Измените Lower и Upper границы для c1 ограничивать цикл от 10 до 14 месяцев, как показано далее.
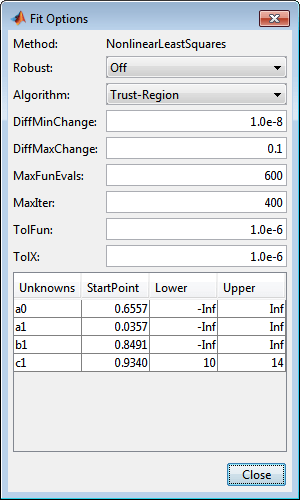
Нажмите Close. Приложение Аппроксимирование Кривыми обновляется.
Наблюдайте новую подгонку и график невязок. При необходимости выберите View > Residuals Plot или используйте кнопку на панели инструментов.
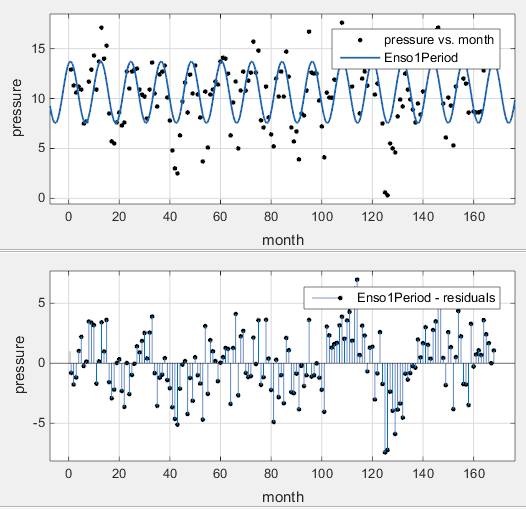
Подгонка представляется разумной для некоторых точек данных, но явно не очень хорошо описывает весь набор данных. Как предсказано, числовые результаты на панели Results (c1=11.94) указать цикл приблизительно 12 месяцев. Однако невязки показывают систематическое периодическое распределение, указывающее, что существует по меньшей мере еще один цикл. Существуют дополнительные циклы, которые вы должны включить в уравнение аппроксимации.
Чтобы уточнить свою подгонку, необходимо добавить дополнительный термин синуса и косинуса к y 1 (x) следующим образом:
и ограничьте верхнюю и нижнюю границы c 2 примерно в два раза больше границ, используемых для c 1.
Повторите подгонку, щелкнув ее правой кнопкой мыши в Table of Fits и выбрав Duplicate ‘Enso1Period’.
Назовите новую Enso2Period подгонки.
Добавьте эти условия к концу предыдущего уравнения:
+a2*cos(2*pi*x/c2)+b2*sin(2*pi*x/c2)
Нажмите Fit Options. Когда вы редактируете пользовательское уравнение, инструмент запоминает ваши опции подгонки. Наблюдайте Lower и Upper границы для c1 все еще ограничивают цикл от 10 до 14 месяцев. Добавьте дополнительные опции подгонки:
Измените Lower и Upper для c2 чтобы быть примерно в два раза больше границ, используемых для c1 (20 <c2<30).
Измените StartPoint на a0 на 5.
Когда вы изменяете каждую настройку, приложение Аппроксимирование Кривыми обновляется. Подгонка и невязки показаны ниже.
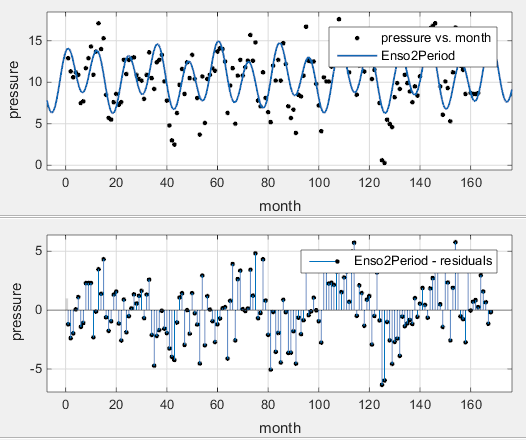
Подгонка выглядит разумной для большинства точек данных. Однако невязки указывают, что вы должны включить другой цикл в уравнение аппроксимации.
В качестве третьей попытки добавьте дополнительный термин синуса и косинуса к y 2 (x)
и ограничьте нижнюю границу c 3 примерно тройной величиной c 1.
Повторите подгонку, щелкнув ее правой кнопкой мыши в Table of Fits и выбрав Duplicate ‘Enso2Period’.
Назовите новую Enso3Period подгонки.
Добавьте эти условия к концу предыдущего уравнения:
+a3*cos(2*pi*x/c3)+b3*sin(2*pi*x/c3)
Нажмите кнопку Fit Options Наблюдайте, что ваши предыдущие опции подгонки все еще присутствуют.
Измените Lower границу для c3 чтобы быть 36, что примерно втрое превышает значение c1.
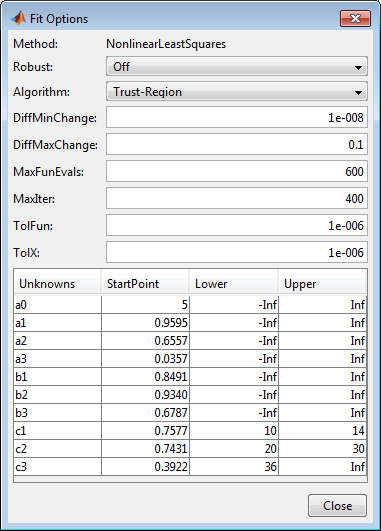
Закройте диалоговое окно. Приложение Аппроксимирование Кривыми обновляется. Подгонка и невязки появляются следующими.
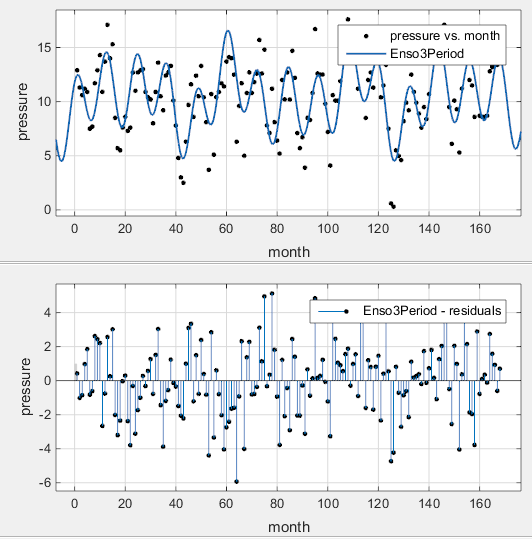
Подгонка является улучшением по сравнению с предыдущими двумя подгонками и, по-видимому, учитывает большинство циклов в наборе данных ENSO. Невязки кажутся случайными для большинства данных, хотя шаблон все еще видим, указывая, что могут присутствовать дополнительные циклы, или можно улучшить установленные амплитуды.
В заключение, Анализ Фурье данных показывает три значимых цикла. Годовой цикл самый сильный, но также присутствуют циклы с периодами примерно 44 и 22 месяца. Эти циклы соответствуют El Nino и Южной осцилляции (ENSO).