Ряд Фурье является суммой синусоидальных и косинусоидных функций, которая описывает периодический сигнал. Он представлен либо в тригонометрической форме, либо в экспоненциальной форме. Тулбокс предоставляет эту тригонометрическую форму Фурье ряда
где модели <reservedrangesplaceholder4> 0, константа (точка пересечения), термин в данных и связан с i = 0 терминов косинуса, w, является основной частотой сигнала, n, являются количеством условий (гармоника) в ряду и 1 ≤ <reservedrangesplaceholder0> ≤ 8.
Для получения дополнительной информации о серии Фурье см. Фурье-анализ и фильтрацию посредством Фурье-преобразования.
Откройте приложение Аппроксимирование Кривыми, введя cftool. Также щелкните Аппроксимированием кривыми на вкладке Приложений.
В приложении Аппроксимирование Кривыми выберите данные кривой (X data и Y data, или просто Y data с индексом).
Приложение Аппроксимирование Кривыми создает подгонку кривой по умолчанию, Polynomial.
Измените тип модели из Polynomial на Fourier.
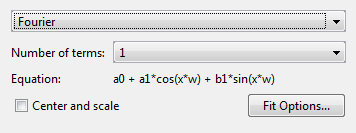
Можно задать следующие опции:
Выберите количество терминов: 1 на 8.
Смотрите на панели Results, чтобы увидеть условия модели, значения коэффициентов и статистику качества подгонки.
(Необязательно) Щелкните Fit Options, чтобы задать начальные значения коэффициентов и ограничения или изменить настройки алгоритма.
Тулбокс вычисляет оптимизированные стартовые точки для моделей серии Фурье на основе текущего набора данных. Можно переопределить начальные точки и задать свои собственные значения в диалоговом окне Опции подгонки (Fit Options).
Для получения дополнительной информации о настройках см. Раздел «Задание опций подгонки» и «Оптимизированные начальные точки».
Для примера сравнения библиотеки Fourier fit с пользовательскими уравнениями, см. Пользовательский нелинейный анализ данных ENSO.
В этом примере показано, как использовать fit функция для подгонки модели Фурье к данным.
Модель библиотеки Фурье является входным параметром к fit и fittype функций. Задайте тип модели fourier далее указывается количество терминов, например 'fourier1' на 'fourier8' .
Этот пример подходит для данных El Nino-Southern Oscillation (ENSO). Данные ENSO состоят из ежемесячных усреднённых различий атмосферного давления между островом Пасхи и Дарвином, Австралия. Это различие движет пассивными ветрами в южном полушарии.
Данные ENSO явно периодичны, что предполагает, что их можно описать серией Фурье. Используйте модели ряда Фурье, чтобы искать периодичность.
Подбор двухсрочной модели Фурье
Загрузите некоторые данные и подбирайте двухсрочную модель Фурье.
load enso; f = fit(month,pressure,'fourier2')
f =
General model Fourier2:
f(x) = a0 + a1*cos(x*w) + b1*sin(x*w) +
a2*cos(2*x*w) + b2*sin(2*x*w)
Coefficients (with 95% confidence bounds):
a0 = 10.63 (10.23, 11.03)
a1 = 2.923 (2.27, 3.576)
b1 = 1.059 (0.01593, 2.101)
a2 = -0.5052 (-1.086, 0.07532)
b2 = 0.2187 (-0.4202, 0.8576)
w = 0.5258 (0.5222, 0.5294)
plot(f,month,pressure)

Доверительные ограничения на a2 и b2 пересечь нуль. Для линейных членов вы не можете быть уверены, что эти коэффициенты отличаются от нуля, поэтому они не помогают с подгонкой. Это означает, что эта модель двух терминов, вероятно, не лучше, чем модель одного термина.
Период измерения
The w термин является мерой периода. 2*pi/w преобразует в период в месяцах, потому что период sin() и cos() является 2*pi .
w = f.w
w = 0.5258
2*pi/w
ans = 11.9497
w очень близко к 12 месяцам, что указывает на годовой период. Наблюдайте это выглядит правильно на графике с peaks примерно 12 месяцев с интервалом.
Подбор восьмеричной модели Фурье
f2 = fit(month,pressure,'fourier8')f2 =
General model Fourier8:
f2(x) =
a0 + a1*cos(x*w) + b1*sin(x*w) +
a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) +
a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) +
a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w) +
a8*cos(8*x*w) + b8*sin(8*x*w)
Coefficients (with 95% confidence bounds):
a0 = 10.63 (10.28, 10.97)
a1 = 0.5668 (0.07981, 1.054)
b1 = 0.1969 (-0.2929, 0.6867)
a2 = -1.203 (-1.69, -0.7161)
b2 = -0.8087 (-1.311, -0.3065)
a3 = 0.9321 (0.4277, 1.436)
b3 = 0.7602 (0.2587, 1.262)
a4 = -0.6653 (-1.152, -0.1788)
b4 = -0.2038 (-0.703, 0.2954)
a5 = -0.02919 (-0.5158, 0.4575)
b5 = -0.3701 (-0.8594, 0.1192)
a6 = -0.04856 (-0.5482, 0.4511)
b6 = -0.1368 (-0.6317, 0.3581)
a7 = 2.811 (2.174, 3.449)
b7 = 1.334 (0.3686, 2.3)
a8 = 0.07979 (-0.4329, 0.5925)
b8 = -0.1076 (-0.6037, 0.3885)
w = 0.07527 (0.07476, 0.07578)
plot(f2,month,pressure)

Период измерения
w = f2.w
w = 0.0753
(2*pi)/w
ans = 83.4736
С f2 модель, период w составляет приблизительно 7 лет.
Исследуйте условия
Проверьте коэффициенты с наибольшей величиной, чтобы найти наиболее важные условия.
a7 и b7 являются самыми большими. Посмотрите на a7 член в модели: a7*cos(7*x*w). 7*w = = 7/7 = цикл 1 год. a7 и b7 указать, что годовой цикл самый сильный.
Точно так же a1 и b1 условия дают 7/1, что указывает на семилетний цикл.
a2 и b2 терминами являются 3,5-летний цикл (7/2). Это сильнее, чем 7-летний цикл, потому что a2 и b2 коэффициенты имеют большую величину, чем a1 и b1.
a3 и b3 довольно сильные условия, указывающие на цикл 7/3 или 2,3 года.
Меньшие условия менее важны для подгонки, такие как a6, b6, a5, и b5.
Обычно потепление Эль-Нино происходит с нерегулярными интервалами от двух до семи лет и длится от девяти месяцев до двух лет. Средняя продолжительность периода составляет пять лет. Результаты модели отражают некоторые из этих периодов.
Задание начальных точек
Тулбокс вычисляет оптимизированные начальные точки для подгонки Фурье на основе текущего набора данных. Модели Фурье-ряда особенно чувствительны к начальным точкам, и оптимизированные значения могут быть точными только для нескольких членов в связанных уравнениях. Можно переопределить начальные точки и задать свои собственные значения.
После изучения условий и графиков, похоже, что 4-летний цикл может присутствовать. Попытайтесь подтвердить это, задав w. Получите значение для w, где 8 лет = 96 месяцев.
w = (2*pi)/96
w = 0.0654
Найдите порядок записей для коэффициентов в модели ('f2') при помощи coeffnames функция.
coeffnames(f2)
ans = 18x1 cell
{'a0'}
{'a1'}
{'b1'}
{'a2'}
{'b2'}
{'a3'}
{'b3'}
{'a4'}
{'b4'}
{'a5'}
{'b5'}
{'a6'}
{'b6'}
{'a7'}
{'b7'}
{'a8'}
{'b8'}
{'w' }
Получите значения текущих коэффициентов.
coeffs = coeffvalues(f2)
coeffs = 1×18
10.6261 0.5668 0.1969 -1.2031 -0.8087 0.9321 0.7602 -0.6653 -0.2038 -0.0292 -0.3701 -0.0486 -0.1368 2.8112 1.3344 0.0798 -0.1076 0.0753
Установите последний коэффициент, w, до 0,065.
coeffs(:,18) = w
coeffs = 1×18
10.6261 0.5668 0.1969 -1.2031 -0.8087 0.9321 0.7602 -0.6653 -0.2038 -0.0292 -0.3701 -0.0486 -0.1368 2.8112 1.3344 0.0798 -0.1076 0.0654
Установите начальные точки для коэффициентов, используя новое значение для w.
f3 = fit(month,pressure,'fourier8', 'StartPoint', coeffs);
Постройте график подгонки, чтобы увидеть, что новое значение для w в f3 не дает лучшую подгонку, чем f2 .
plot(f3,month,pressure) hold on plot(f2, 'b') hold off legend( 'Data', 'f3', 'f2')

Опции поиска Подгонки
Найдите доступные опции подгонки с помощью fitoptions(modelname), где modelname является типом модели fourier далее указывается количество терминов, например 'fourier1' на 'fourier8' .
fitoptions('fourier8')ans =
Normalize: 'off'
Exclude: []
Weights: []
Method: 'NonlinearLeastSquares'
Robust: 'Off'
StartPoint: [1x0 double]
Lower: [1x0 double]
Upper: [1x0 double]
Algorithm: 'Trust-Region'
DiffMinChange: 1.0000e-08
DiffMaxChange: 0.1000
Display: 'Notify'
MaxFunEvals: 600
MaxIter: 400
TolFun: 1.0000e-06
TolX: 1.0000e-06
Если вы хотите изменить опции подгонки, такие как начальные значения коэффициентов и ограничения, соответствующие вашим данным, или изменить настройки алгоритма, смотрите опции для NonlinearLastSquares на fitoptions страница с описанием.
fit | fitoptions | fittype