Метод наименьших квадратов Подбора кривой

Введение

Программное обеспечение Curve Fitting Toolbox™ использует метод наименьших квадратов при подгонке данных. Подбор кривой требует параметрической модели, которая связывает данные отклика с данными предиктора с одним или несколькими коэффициентами. Результатом процесса подгонки является оценка коэффициентов модели.

Чтобы получить оценки коэффициентов, метод методом наименьших квадратов минимизирует суммированный квадрат невязок. Невязка для i-го _ri точки данных определяется как различие между наблюдаемым значением отклика _yi и установленным значением отклика _ŷi, и идентифицируется как ошибка, связанная с данными.

$\begin{array}{l} r_{i} = y_{i} - {\hat{y}}_{i} \\ остаточный = данные - подгонка \end{array}$

Суммированный квадрат невязок задается как

$S = \sum_{i = 1}^{n} r_{i}^{2} = \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}$

где n - количество точек данных, включенных в подгонку, и S - сумма оценки ошибки квадратов. Поддерживаемые типы подбора кривой методом наименьших квадратов включают:

Линейный метод наименьших квадратов
Взвешенный линейный метод наименьших квадратов
Устойчивые наименьшие квадраты
Нелинейные методы наименьших квадратов

Распределения ошибок

При подгонке данных, которые содержат случайные изменения, существуют два важных предположения, которые обычно делаются относительно ошибки:

Ошибка существует только в данных отклика, а не в данных предиктора.
Ошибки случайны и следуют нормальному (Гауссову) распределению с нулем среднего и постоянного отклонения, σ².

Второе предположение часто выражается как

$e r r o r \sim N (0, σ^{2})$

Ошибки приняты обычно распределенными, потому что нормальное распределение часто обеспечивает адекватное приближение к распределению многих измеренных величин. Несмотря на то, что метод аппроксимации методом наименьших квадратов не принимает нормально распределенные ошибки при вычислении оценок параметров, метод лучше всего работает для данных, которые не содержат большое количество случайных ошибок с экстремальными значениями. Нормальное распределение является одним из распределений вероятностей, в которых экстремальные случайные ошибки редки. Однако статистические результаты, такие как ограничения доверия и предсказания, требуют нормально распределенных ошибок для их валидности.

Если среднее значение ошибок равно нулю, то ошибки являются чисто случайными. Если среднее значение не является нулем, то может быть, что модель не является правильным выбором для ваших данных, или ошибки не являются чисто случайными и содержат систематические ошибки.

Постоянное отклонение в данных подразумевает, что «разброс» ошибок является постоянным. Данные, которые имеют то же отклонение, иногда считаются equal quality.

Предположение, что случайные ошибки имеют постоянное отклонение, не неявно для взвешенной регрессии методом наименьших квадратов. Вместо этого принято, что веса, предусмотренные в процедуре подгонки, правильно указывают на различные уровни качества, существующие в данных. Веса затем используются, чтобы настроить количество влияния, которое каждая точка данных оказывает на оценки подобранных коэффициентов, на соответствующий уровень.

Линейные методы наименьших квадратов

Программное обеспечение Curve Fitting Toolbox использует линейный метод наименьших квадратов, чтобы подгонять линейную модель к данным. Линейная модель определяется как уравнение, которое линейно в коэффициентах. Например, полиномы линейны, но Гауссов нет. Чтобы проиллюстрировать линейный процесс подбора кривой методом наименьших квадратов, предположим, что у вас есть n точки данных, которые могут быть смоделированы полиномом первой степени.

$y = p_{1} x + p_{2}$

Чтобы решить это уравнение для неизвестных коэффициентов p 1 и _p 2, вы записываете S как систему n одновременных линейных уравнений в двух неизвестных. Если n больше, чем количество неизвестных, то система уравнений переопределена.

$S = \sum_{i = 1}^{n} {(y_{i} - (p_{1} x_{i} + p_{2}))}^{2}$

Поскольку процесс подбора кривой методом наименьших квадратов минимизирует суммированный квадрат невязок, коэффициенты определяются путем дифференцирования S относительно каждого параметра и установки результата равным нулю.

$\begin{array}{l} \frac{\partial S}{\partial p_{1}} = - 2 \sum_{i = 1}^{n} x_{i} (y_{i} - (p_{1} x_{i} + p_{2})) = 0 \\ \frac{\partial S}{\partial p_{2}} = - 2 \sum_{i = 1}^{n} (y_{i} - (p_{1} x_{i} + p_{2})) = 0 \end{array}$

Оценки истинных параметров обычно представлены b. Подставляя b 1 и _b 2 для p 1 и p 2, предыдущие уравнения становятся

$\begin{matrix} \sum x_{i} (y_{i} - (b_{1} x_{i} + b_{2})) = 0 \\ \sum (y_{i} - (b_{1} x_{i} + b_{2})) = 0 \end{matrix}$

где суммирования выполняются от i = 1 до n. Нормальные уравнения заданы как

$\begin{matrix} b_{1} \sum x_{i}^{2} + b_{2} \sum x_{i} = \sum x_{i} y_{i} \\ b_{1} \sum x_{i} + n b_{2} = \sum y_{i} \end{matrix}$

Решение для b 1

$b_{1} = \frac{n \sum x_{i} y_{i} - \sum x_{i} \sum y_{i}}{n \sum x_{i}^{2} - {(\sum x_{i})}^{2}}$

Решение для b 2 с использованием значения _b 1

$b_{2} = \frac{1}{n} (\sum y_{i} - b_{1} \sum x_{i})$

Как видим, оценка коэффициентов p 1 и _p 2 требует всего нескольких простых вычислений. Расширение этого примера до полинома более высокой степени просто, хотя бит утомительно. Все, что требуется, является дополнительным нормальным уравнением для каждого линейного члена, добавленного к модели.

В матричном виде линейные модели заданы формулой

y = X β + ε

где

y является n вектором откликов -by-1 .
β - вектор коэффициентов m -by-1.
X - n матрица проекта m для модели.
.r- вектор n -by-1 ошибок.

Для полинома первой степени n уравнения в двух неизвестных выражены в терминах y, X и β как

$[\begin{matrix} y_{1} \\ y_{2} \\ y_{3} \\ . \\ . \\ . \\ y_{n} \end{matrix}] = [\begin{matrix} x_{1} 1 \\ x_{2} 1 \\ x_{3} 1 \\ . \\ . \\ . \\ x_{n} 1 \end{matrix}] \times [\begin{array}{l} p_{1} \\ p_{2} \end{array}]$

Решение методом наименьших квадратов к задаче является векторная b, которая оценивает неизвестный вектор коэффициентов β. Нормальные уравнения заданы как

(X^TX) b = X^Ty

где X^T - транспонирование матричного X проекта. Решая для b,

b = (X^TX)^–1 X^Ty

Используйте MATLAB^® оператор обратной косой черты (mldivide) для решения системы одновременных линейных уравнений для неизвестных коэффициентов. Потому что инвертирование X^TX может привести к недопустимым ошибкам округления, оператор обратной косой черты использует QR разложение с поворотом, что является очень стабильным алгоритмом в численном отношении. Для получения дополнительной информации об операторе обратной косой черты и QR разложении см. раздел «Арифметические операции».

Можно включить b обратно в формулу модели, чтобы получить предсказанные значения отклика, ŷ.

ŷ = Xb = Hy

H = X (X^TX)^–1 X^T

Шляпа (circumflex) над буквой обозначает оценку параметра или предсказание из модели. Матрица проекций H называется матрицей шляпы, потому что она помещает шляпу на y.

Невязки заданы как

r = y – ŷ = (1–<reservedrangesplaceholder1>) y

Взвешенные наименьшие квадраты

Обычно принято, что данные отклика имеют равное качество и, следовательно, имеют постоянное отклонение. Если это предположение нарушено, на вашу подгонку могут чрезмерно влиять данные низкого качества. Чтобы улучшить подгонку, можно использовать взвешенную регрессию методом наименьших квадратов, где дополнительный масштабный коэффициент (вес) включен в процесс подгонки. Взвешенная регрессия методом наименьших квадратов минимизирует оценку ошибки

$s = \sum_{i = 1}^{n} w_{i} {(y_{i} - {\hat{y}}_{i})}^{2}$

где _wi веса. Веса определяют, насколько каждое значение отклика влияет на окончательные оценки параметра. Высококачественная точка данных влияет на подгонку больше, чем низкокачественная точка данных. Взвешивание ваших данных рекомендуется, если веса известны или если есть обоснование, что они следуют определенной форме.

Веса изменяют выражение для оценок параметров b следующим образом,

$b = \hat{β} = {(X^{T} W X)}^{- 1} X^{T} W y$

где W задается диагональными элементами матричной w веса.

Можно часто определять, не являются ли отклонения постоянными, подгонкой данных и графическим изображением невязки. На графике, показанном ниже, данные содержат данные репликации различного качества, и подгонка принята правильной. Данные о плохом качестве выявляются в графике невязок, который имеет форму «воронки», где маленькие значения предиктора приводят к большему рассеянию значений отклика, чем большие значения предиктора.

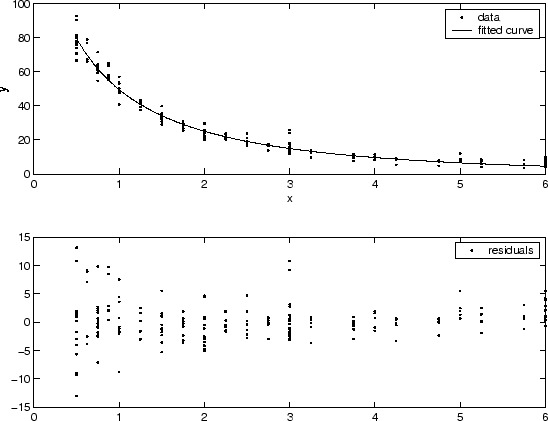
Веса, которые вы поставляете, должны преобразовать отклонения отклика в постоянное значение. Если вы знаете отклонения ошибок измерения в ваших данных, то веса заданы как

$w_{i} = 1 / σ_{i}^{2}$

Или, если у вас есть только оценки переменной ошибки для каждой точки данных, обычно достаточно использовать эти оценки вместо истинного отклонения. Если вы не знаете отклонений, достаточно задать веса в относительной шкале. Обратите внимание, что срок полного отклонения оценивается, даже когда веса были заданы. В этом случае веса определяют относительный вес каждой точки подгонки, но не берутся, чтобы задать точное отклонение каждой точки.

Для примера, если каждая точка данных является средним значением нескольких независимых измерений, возможно, имеет смысл использовать это количество измерений в качестве весов.

Устойчивые наименьшие квадраты

Обычно принято, что ошибки отклика следуют нормальному распределению, и что экстремальные значения редки. Тем не менее, экстремальные значения, называемые выбросами, действительно происходят.

Основным недостатком подбора кривой методом наименьших квадратов является ее чувствительность к выбросам. Выбросы оказывают большое влияние на подгонку, потому что квадратура невязок увеличивает эффекты этих экстремальных точек данных. Чтобы минимизировать влияние выбросов, вы можете подогнать свои данные с помощью устойчивой регрессии методом наименьших квадратов. Тулбокс предоставляет эти два устойчивых метода регрессии:

Наименьшие абсолютные остатки (LAR) - метод LAR находит кривую, которая минимизирует абсолютное различие невязок, а не квадратные различия. Поэтому экстремальные значения оказывают меньшее влияние на подгонку.
Веса Bisquare - этот метод минимизирует взвешенную сумму квадратов, где вес, заданный каждой точке данных, зависит от того, насколько далеко точка находится от установленной линии. Точки рядом с линией получают полный вес. Точки дальше от линии получают уменьшенный вес. Точки, которые находятся дальше от линии, чем ожидалось бы случайным образом, получают нулевой вес.
В большинстве случаев метод веса bisquare предпочтителен по сравнению с LAR, потому что он одновременно стремится найти кривую, которая подходит для основной массы данных с помощью обычного подхода методом наименьших квадратов, и это минимизирует эффект выбросов.

Устойчивый подбор кривой с весами bisquare использует итерационно переоцененный алгоритм наименьших квадратов и следует этой процедуре:

Подгонка модели по взвешенным наименьшим квадратам.
Вычислите скорректированные невязки и стандартизируйте их. Скорректированные невязки заданы как
$r_{a d j} = \frac{r_{i}}{\sqrt{1 - h_{i}}}$
_ri являются обычными невязками методом наименьших квадратов, и _hi являются рычагами, которые регулируют невязки путем уменьшения веса точек данных с высоким коэффициентом использования, которые оказывают большой эффект на аппроксимацию методом наименьших квадратов. Стандартизированные скорректированные невязки даны
$u = \frac{r_{a d j}}{K s}$
K является постоянной настройки, равной 4,685, и s является устойчивым стандартным отклонением, заданным MAD/0,6745, где MAD является медианным абсолютным отклонением невязок.
Вычислите устойчивые веса как функцию от u. Веса bisquare заданы как
$w_{i} = {\begin{matrix} {(1 - {(u_{i})}^{2})}^{2} & | u_{i} | < 1 \\ 0 & | u_{i} | \geq 1 \end{matrix}$
Обратите внимание, что если вы поставляете свой собственный вектор регрессионного веса, конечный вес является продуктом устойчивого веса и регрессионного веса.
Если подгонка сходится, все сделано. В противном случае выполните следующую итерацию процедуры аппроксимации путем возврата к первому шагу.

Показанные ниже графики сравнивают регулярную линейную подгонку с устойчивой подгонкой с использованием весов bisquare. Заметьте, что устойчивая подгонка следует основной массе данных и не сильно зависит от выбросов.

Вместо минимизации эффектов выбросов при помощи устойчивой регрессии можно пометить точки данных, которые будут исключены из подгонки. Дополнительные сведения см. в разделе Удаление Выбросах.

Нелинейные методы наименьших квадратов

Программное обеспечение Curve Fitting Toolbox использует формулировку нелинейного метода наименьших квадратов, чтобы соответствовать нелинейной модели данным. Нелинейная модель определяется как уравнение, которое нелинейно в коэффициентах или как комбинация линейных и нелинейных в коэффициентах. Для примера, Гауссов отношения полиномов и степени функций являются нелинейными.

В матричном виде нелинейные модели заданы формулой

y = f (X, β) +

где

y является n вектором откликов -by-1.
f является функцией β и X.
β - вектор коэффициентов m -by-1.
X - n матрица проекта m для модели.
.r- вектор n -by-1 ошибок.

Нелинейные модели сложнее подгонять, чем линейные модели, потому что коэффициенты не могут быть оценены с помощью простых матричных методов. Вместо этого требуется итерационный подход, следующий за этими шагами:

Начните с начальной оценки для каждого коэффициента. Для некоторых нелинейных моделей предусмотрен эвристический подход, который производит разумные стартовые значения. Для других моделей предусмотрены случайные значения на интервале [0,1].
Создайте подобранную кривую для текущего набора коэффициентов. Установленное ŷ значения отклика задается как
ŷ = f (X, b)
и включает вычисление якобиана f (X,b), которое определяется как матрица частных производных, взятых относительно коэффициентов.
Скорректируйте коэффициенты и определите, улучшается ли подгонка. Направление и величина регулировки зависят от алгоритма аппроксимации. Тулбокс предоставляет следующие алгоритмы:
- Доверительная область - это алгоритм по умолчанию, и он должен использоваться, если вы задаете ограничения коэффициентов. Это может решить трудные нелинейные задачи более эффективно, чем другие алгоритмы, и это представляет улучшение по сравнению с популярным алгоритмом Левенберга-Марквардта.
- Левенберг-Марквардт - Этот алгоритм используется в течение многих лет и доказал, что работает большую часть времени для широкой области значений нелинейных моделей и начальных значений. Если алгоритм доверительной области не дает разумной подгонки, и у вас нет ограничений по коэффициентам, вы должны попробовать алгоритм Левенберга-Марквардта.
Итерация процесса путем возврата к шагу 2 до тех пор, пока подгонка не достигнет заданного критерия сходимости.

Для нелинейных моделей можно использовать веса и устойчивый подбор кривой, и процесс аппроксимации изменяется соответствующим образом.

Из-за особенностей процесса приближения ни один алгоритм не является безупречным для всех нелинейных моделей, наборов данных и начальных точек. Поэтому, если вы не достигаете разумной подгонки с помощью начальных точек по умолчанию, алгоритма и критериев сходимости, следует поэкспериментировать с различными опциями. Описание изменения опций по умолчанию см. в разделе «Задание параметров подгонки и оптимизированные начальные точки». Поскольку нелинейные модели могут быть особенно чувствительны к начальным точкам, это должен быть первая опция подгонки.

Устойчивый подбор кривой

Открыть Live Script

В этом примере показано, как сравнить эффекты исключения выбросов и устойчивого подбора кривой. Пример показывает, как исключить выбросы на произвольном расстоянии, больше 1,5 стандартных отклонений от модели. Затем шаги сравнивают удаление выбросов с указанием устойчивой подгонки, которая дает меньший вес выбросам.

Создайте базовый синусоидальный сигнал:

xdata = (0:0.1:2*pi)'; 
y0 = sin(xdata);

Добавьте шум к сигналу с неконстантным отклонением.

% Response-dependent Gaussian noise
gnoise = y0.*randn(size(y0));

% Salt-and-pepper noise
spnoise = zeros(size(y0)); 
p = randperm(length(y0));
sppoints = p(1:round(length(p)/5));
spnoise(sppoints) = 5*sign(y0(sppoints));

ydata = y0 + gnoise + spnoise;

Подгоните зашумленные данные с помощью базовой синусоидальной модели и задайте 3 выходных аргумента, чтобы получить подходящую информацию, включая невязки.

f = fittype('a*sin(b*x)'); 
[fit1,gof,fitinfo] = fit(xdata,ydata,f,'StartPoint',[1 1]);

Исследуйте информацию в структуре fitinfo.

fitinfo

fitinfo = struct with fields:
           numobs: 63
         numparam: 2
        residuals: [63x1 double]
         Jacobian: [63x2 double]
         exitflag: 3
    firstorderopt: 0.0883
       iterations: 5
        funcCount: 18
     cgiterations: 0
        algorithm: 'trust-region-reflective'
         stepsize: 4.1539e-04
          message: 'Success, but fitting stopped because change in residuals less than tolerance (TolFun).'

Получите невязки от структуры fitinfo.

residuals = fitinfo.residuals;

Идентифицируйте «выбросы» как точки на произвольном расстоянии, больше 1,5 стандартных отклонений от базовой модели, и обновляйте данные с исключенными выбросами.

I = abs( residuals) > 1.5 * std( residuals );
outliers = excludedata(xdata,ydata,'indices',I);

fit2 = fit(xdata,ydata,f,'StartPoint',[1 1],...
           'Exclude',outliers);

Сравните эффект исключения выбросов с эффектом придания им меньшего веса bisquare в устойчивой подгонке.

fit3 = fit(xdata,ydata,f,'StartPoint',[1 1],'Robust','on');

Постройте график данных, выбросов и результатов подгонки. Задайте информативную легенду.

plot(fit1,'r-',xdata,ydata,'k.',outliers,'m*') 
hold on
plot(fit2,'c--')
plot(fit3,'b:')
xlim([0 2*pi])
legend( 'Data', 'Data excluded from second fit', 'Original fit',...
    'Fit with points excluded', 'Robust fit' )
hold off

Figure contains an axes. The axes contains 5 objects of type line. These objects represent Data, Data excluded from second fit, Original fit, Fit with points excluded, Robust fit.

Постройте график невязок для двух подгонка с учетом выбросов:

figure 
plot(fit2,xdata,ydata,'co','residuals') 
hold on
plot(fit3,xdata,ydata,'bx','residuals')
hold off

Figure contains an axes. The axes contains 4 objects of type line. These objects represent data, zero line.

Документация