Фон автоматической дифференциации

Что такое автоматическая дифференциация?

Автоматическая дифференциация (также известная как autodiff, AD или algorithmic differentiation) является широко используемым инструментом глубокого обучения. Смотрите книги по автоматической дифференциации. Это особенно полезно для создания и настройки сложных моделей глубокого обучения без необходимости вычислять производные вручную для оптимизации. Для примеров, показывающих, как создать и настроить модели глубокого обучения, циклы обучения и функции потерь, смотрите, Задайте Пользовательские Циклы Обучения, Функции Потерь и Сети.

Автоматическая дифференциация является набором методов для оценки производных (градиентов). Метод использует символьные правила для дифференцирования, которые более точны, чем конечные дифференциальные приближения. В отличие от чисто символьного подхода, автоматическая дифференциация оценивает выражения численно в начале расчетов, а не выполняет большие символьные расчеты. Другими словами, автоматическая дифференциация оценивает производные по конкретным числовым значениям; он не создает символьных выражений для производных.

Forward mode оценивает числовую производную путем выполнения элементарных производных операций одновременно с операциями оценки самой функции. Как подробно описано в следующем разделе, программное обеспечение выполняет эти расчеты на вычислительном графике.
Reverse mode автоматическая дифференциация использует расширение вычислительного графика прямого режима, чтобы разрешить расчет градиента обратным обходом графика. Когда программное обеспечение запускает код, чтобы вычислить функцию и ее производную, оно записывает операции в структуру данных, называемую trace.

Как отметили многие исследователи (для примера, Baydin, Pearlmutter, Radul и Siskind [1]), для скалярной функции многих переменных обратный режим вычисляет градиент более эффективно, чем прямой режим. Поскольку функция потерь глубокого обучения является скалярной функцией всех весов, Deep Learning Toolbox™ автоматическая дифференциация использует обратный режим.

Режим переадресации

Рассмотрим задачу оценки этой функции и ее градиента:

$f (x) = x_{1} \exp (- \frac{1}{2} (x_{1}^{2} + x_{2}^{2})) .$

Автоматическая дифференциация работает в конкретных точках. В этом случае примите x 1 = 2, _x 2 = 1/2.

Следующий вычислительный график кодирует вычисление f функции (x).

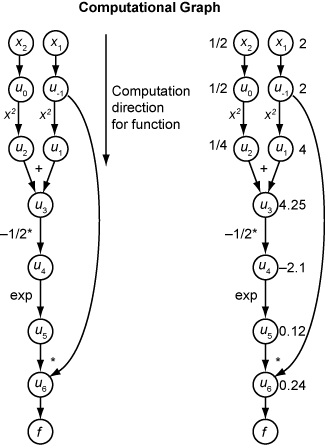
Чтобы вычислить градиент f (x) с помощью прямого режима, вы вычисляете тот же график в том же направлении, но изменяете расчет на основе элементарных правил дифференциации. Чтобы еще больше упростить вычисление, вы заполняете значение производной от каждой подэкспрессии _ui как вы идете. Чтобы вычислить весь градиент, необходимо пройти график дважды, один раз для частной производной относительно каждой независимой переменной. Каждая подэкспрессия в правиле цепи имеет числовое значение, поэтому все выражение имеет тот же вид графика оценки, что и сама функция.

Расчет является повторным применением правила цепи. В этом примере производная f относительно x 1 расширяется до этого выражения:

$\begin{matrix} \frac{d f}{d x_{1}} = \frac{d u_{6}}{d x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial u_{3}} \frac{\partial u_{3}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial u_{3}} \frac{\partial u_{3}}{\partial u_{1}} \frac{\partial u_{1}}{\partial x_{1}} . \end{matrix}$

Давайте ${\dot{u}}_{i}$ представляют производную _ui выражения относительно x 1. Используя вычисленные значения _ui из вычисления функции, вы вычисляете частную производную f относительно _x 1 как показано на следующем рисунке. Заметьте, что все значения ${\dot{u}}_{i}$ станет доступным, когда вы пройдете график сверху вниз.

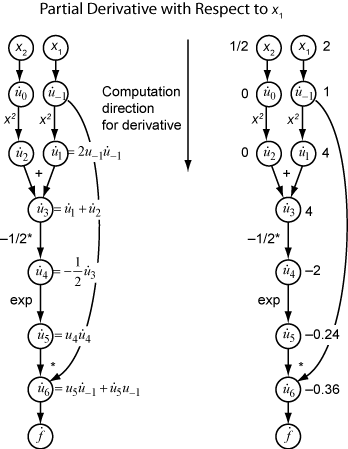
Чтобы вычислить частную производную относительно x 2, вы проходите аналогичный вычислительный график. Поэтому, когда вы вычисляете градиент функции, количество обходов графика совпадает с количеством переменных. Этот процесс слишком медлен для типичных применений глубокого обучения, которые имеют тысячи или миллионы переменных.

Обратный режим

Обратный режим использует один прямой ход вычислительного графика, чтобы настроить трассировку. Затем он вычисляет весь градиент функции в одном обходе графика в противоположном направлении. Для применений глубокого обучения этот режим намного эффективнее.

Теория за обратной модой также основана на правиле цепи, наряду со связанными смежными переменными, обозначенными как overbar. Смежная переменная для _ui

${\bar{u}}_{i} = \frac{\partial f}{\partial u_{i}} .$

В терминах вычислительного графика каждая исходящая стрела из переменной вносит вклад в соответствующую смежную переменную своим термином в правиле цепи. Например, u переменной _-1 имеет исходящие стрелки к двум переменным, _u 1 и u 6. График имеет связанное уравнение

$\begin{matrix} \frac{\partial f}{\partial u_{- 1}} = \frac{\partial f}{\partial u_{1}} \frac{\partial u_{1}}{\partial u_{- 1}} + \frac{\partial f}{\partial u_{6}} \frac{\partial u_{6}}{\partial u_{- 1}} \\ = {\bar{u}}_{1} \frac{\partial u_{1}}{\partial u_{- 1}} + {\bar{u}}_{6} \frac{\partial u_{6}}{\partial u_{- 1}} . \end{matrix}$

В этом вычислении, напоминая, что $u_{1} = u_{- 1}^{2}$ и u 6 = _u ₅ u -1, вы получаете

${\bar{u}}_{- 1} = {\bar{u}}_{1} 2 u_{- 1} + {\bar{u}}_{6} u_{5} .$

Во время прямого обхода графика программное обеспечение вычисляет промежуточные переменные _ui. Во время обратного обхода, начиная с seed значения ${\bar{u}}_{6} = \frac{\partial f}{\partial f} = 1$ обратный режим расчета получает смежные значения для всех переменных. Поэтому обратный режим вычисляет градиент всего за одно расчет, сохраняя много времени по сравнению с прямым режимом.

Следующий рисунок показывает расчет градиента в обратном режиме для функции

$f (x) = x_{1} \exp (- \frac{1}{2} (x_{1}^{2} + x_{2}^{2})) .$

Снова, вычисление принимает x 1 = 2, _x 2 = 1/2. Расчет обратного режима основан на ui значениях, которые получаются во время расчета функции в исходном вычислительном графике. В правом фрагменте рисунка вычисленные значения смежных переменных появляются рядом с смежными именами переменных с помощью формул из левого фрагмента рисунка.

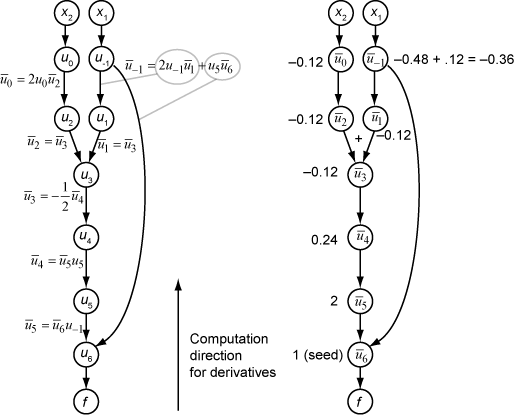
Окончательные значения градиента появляются как ${\bar{u}}_{0} = \frac{\partial f}{\partial u_{0}} = \frac{\partial f}{\partial x_{2}}$ и ${\bar{u}}_{- 1} = \frac{\partial f}{\partial u_{- 1}} = \frac{\partial f}{\partial x_{1}}$ .

Для получения дополнительной информации смотрите Baydin, Pearlmutter, Radul и Siskind [1] или статью Википедии об автоматической дифференциации [2].

Ссылки

[1] Байдин, А. Г., Б. А. Перлмуттер, А. А. Радул, и Я. М. Сискинд. «Автоматическая дифференциация в машинном обучении: опрос». Журнал исследований машинного обучения, 18 (153), 2018, стр. 1-43. Доступно в https://arxiv.org/abs/1502.05767.

[2] Автоматическая дифференциация. Википедия. Доступно в https://en.wikipedia.org/wiki/Automatic_differentiation.

См. также

dlarray | dlfeval | dlgradient | dlnetwork

Документация