Документация

Сетевая архитектура

Обобщенная регрессионная нейронная сеть (GRNN) часто используется для приближения функций. Он имеет радиальный базовый слой и специальный линейный слой.

Архитектура GRNN показана ниже. Он похож на радиальную сеть базиса, но имеет несколько другой второй слой.

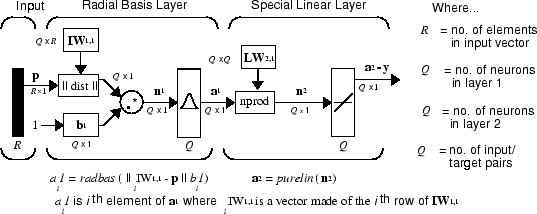
Здесь окно nprod, показанное выше (функция кода normprod) производит S² элементы в векторе n². Каждый элемент является точечным продуктом строки LW^2,1 и вектор входа a¹, все нормированные по сумме элементов массива¹. Например, предположим, что

LW{2,1}= [1 -2;3 4;5 6];
a{1} = [0.7;0.3];

Тогда

aout = normprod(LW{2,1},a{1})
aout =
    0.1000
    3.3000
    5.3000

Первый слой просто так для newrbe сети. У него столько нейронов, сколько векторов ввода/мишени в P. В частности, веса первого слоя установлены на P '. Смещение b¹ устанавливается на вектор-столбец 0 .8326/ SPREAD. Пользователь выбирает SPREAD, расстояние, на которое входной вектор должен находиться от вектора веса нейрона, должно быть 0,5.

Снова, первый слой работает так же, как и newrbe слой радиального базиса, описанный выше. Взвешенный вход каждого нейрона является расстоянием между входным вектором и его вектором веса, вычисленным с dist. Чистый вход каждого нейрона является продуктом его взвешенного входа с его смещением, вычисленным с netprod. Выход каждого нейрона является его чистым входом, прошедшим radbas. Если вектор веса нейрона равен входному вектору (транспонированному), его взвешенный вход будет равен 0, его чистый вход будет равен 0, и его выход будет равен 1. Если вектор веса нейрона является расстоянием spread из входного вектора будет spread его взвешенный вход, и его чистый вход будет sqrt (− log (.5)) (или 0,8326). Поэтому его выход составит 0,5.

Второй слой также имеет столько нейронов, сколько входных/целевых векторов, но здесь LW{2,1} установлено в T.

Предположим, что у вас есть входной вектор p, близкий к p i, одному из входных векторов среди входных векторов/целевых пар, используемых при разработке весов слоя 1. Этот вход p создает слой 1 аⁱ выход близок к 1. Это приводит к выходу слоя 2, близкому к t i, одному из целевых объектов, используемых для формирования весов слоя 2.

Больший spread приводит к большой площади вокруг входного вектора, где нейроны слоя 1 будут отвечать значительными выходами. Поэтому, если spread является маленькой функция радиального базиса очень крутая, так что нейрон с вектором веса, ближайшим к входу, будет иметь намного больший выход, чем другие нейроны. Сеть имеет тенденцию отвечать с целевым вектором, сопоставленным с ближайшим вектором входа проекта.

Как spread становится больше, наклон функции радиального базиса становится более плавным, и несколько нейронов могут реагировать на вектор входа. Сеть затем действует так, как будто она принимает взвешенное среднее значение между целевыми векторами, чья конструкция входа векторы ближе всего к новому вектору входа. Как spread становится больше и больше нейронов вносят свой вклад в среднее значение, в результате чего функция сети становится более гладкой.

Проект (newgrnn)

Вы можете использовать функцию newgrnn для создания GRNN. Например, предположим, что три входных и три целевых вектора заданы как

P = [4 5 6];
T = [1.5 3.6 6.7];

Теперь вы можете получить GRNN с

net = newgrnn(P,T);

и моделируйте его с

P = 4.5;
v = sim(net,P);

Можно хотеть также попробовать приближение функций GRNN.