Розенблатт [Rose61] создал много изменения перцептрона. Одной из самых простых была однослойная сеть, веса и смещения которой можно было бы обучить, чтобы получить правильный целевой вектор, когда представлен с соответствующим входным вектором. Используемый метод обучения называется правилом обучения перцептронов. Перцептрон вызвал большой интерес из-за своей способности обобщать из своих обучающих векторов и учиться из первоначально случайным образом распределенных соединений. Перцептроны особенно подходят для простых задач в классификации шаблонов. Они являются быстрыми и надежными сетями для задач, которые они могут решить. В сложение понимание операций перцептрона обеспечивает хороший базисный для понимания более сложных сетей.
Обсуждение перцептронов в этом разделе обязательно краткое. Для более подробного обсуждения см. главу 4 «Правило обучения перцептронов» [HDB1996], в которой обсуждается использование нескольких слоев перцептронов для решения более сложных задач, выходящих за рамки возможностей одного слоя.
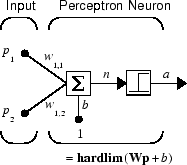
Нейрон перцептрона, который использует жестко-предельную передаточную функцию hardlim, показано ниже.
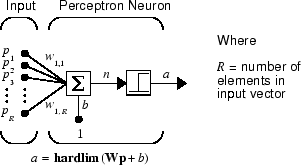
Каждый внешний вход взвешивается соответствующим весом w 1j, и сумма взвешенных входов отправляется в передаточную функцию с жестким пределом, которая также имеет вход 1, переданный ей через смещение. Передаточная функция с жестким пределом, которая возвращает 0 или 1, показана ниже.
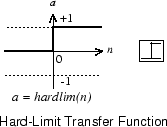
Нейрон перцептрона производит 1, если вход сети в передаточную функцию равен или больше 0; в противном случае это создает 0.
Жесткий предел передаточной функции дает перцептрону возможность классифицировать вход вектора путем деления входного пространства на две области. В частности, выходы будут равны 0, если чистый входной n меньше 0, или 1, если чистый входной n равен 0 или больше. Следующие рисунки показывают входное пространство нейрона с двумя входами жесткого предела с весами w 1,1 = − 1, w 1,2 = 1 и смещением b = 1.
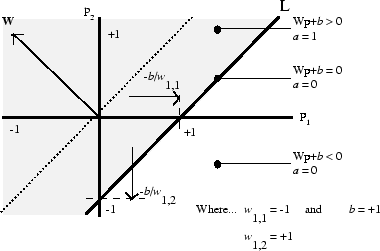
Две области классификации формируются контуром принятия решения L в
Wp + b = 0. Эта линия перпендикулярна матрице W веса и смещена согласно b смещения. Входные векторы выше и слева от линии L приведут к чистому входу, большему 0 и, следовательно, заставляют нейрон с жестким пределом выводить 1. Входные векторы ниже и справа от линии L заставляют нейрон выводить 0. Можно выбрать значения веса и смещения для ориентации и перемещения разделительной линии так, чтобы классифицировать входное пространство по желанию.
Нейроны с жесткими ограничениями без смещения всегда будут иметь классификационную линию, проходящую через источник. Добавление смещения позволяет нейрону решить проблемы, где два набора входа векторов не расположены на разных сторонах источника. Смещение позволяет смещать контур принятия решений от источника, как показано на графике выше.
Можно хотеть запустить пример программу nnd4db. С его помощью можно переместить контур принятия решений, выбрать новые входы для классификации и увидеть, как повторное применение правила обучения приводит к сети, которая действительно классифицирует входные векторы правильно.
Сеть перцептронов состоит из одного слоя S нейроны перцептрона, соединенные с входами R через набор wi,j весов, как показано ниже в двух формах. Как и прежде, сетевые индексы i и j указывают, что wi,j является силой связи с j-го входа до i-го нейрона.
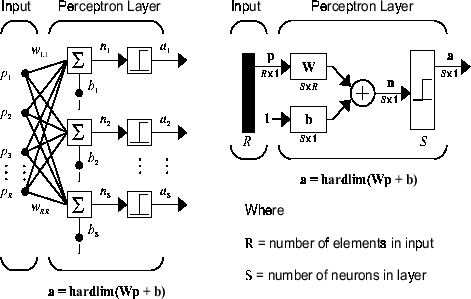
Описанное вскоре правило обучения перцептрон способно обучать только один слой. Таким образом, здесь рассматриваются только однослойные сети. Это ограничение накладывает ограничения на расчеты, которые может выполнить перцептрон. Типы задач, которые способны решить перцептроны, обсуждаются в Limitations и Cautions.
Можно создать перцептрон со следующими:
net = perceptron; net = configure(net,P,T);
где входные параметры следующие:
P - R-на-Q матрица Q входных векторов R элементов каждый.
T - S-на-Q матрица Q-целевых векторов S элементов каждого.
Обычно, hardlim функция используется в перцептронах, поэтому она является функцией по умолчанию.
Следующие команды создают сеть перцептронов с одним одноэлементным вектором входа со значениями 0 и 2 и одним нейроном с выходами, которые могут быть либо 0, либо 1:
P = [0 2]; T = [0 1]; net = perceptron; net = configure(net,P,T);
Можно увидеть, какая сеть была создана, выполнив следующую команду:
inputweights = net.inputweights{1,1}
который дает
inputweights =
delays: 0
initFcn: 'initzero'
learn: true
learnFcn: 'learnp'
learnParam: (none)
size: [1 1]
weightFcn: 'dotprod'
weightParam: (none)
userdata: (your custom info)
Функция обучения по умолчанию является learnp, который обсуждается в Perceptron Learning Rule (learnp). Чистый вход в hardlim передаточная функция dotprod, который генерирует продукт входного вектора и матрицы веса и добавляет смещение, чтобы вычислить вход сети.
Функция инициализации по умолчанию initzero используется для установки начальных значений весов равными нулями.
Точно так же,
biases = net.biases{1}
дает
biases =
initFcn: 'initzero'
learn: 1
learnFcn: 'learnp'
learnParam: []
size: 1
userdata: [1x1 struct]
Вы можете увидеть, что инициализация по умолчанию для смещения также является 0.
Перцептроны обучаются на примерах желаемого поведения. Желаемое поведение может быть суммировано набором входных, выходных пар
где p - вход в сеть, и t - соответствующий правильный (целевой) выход. Цель состоит в том, чтобы уменьшить ошибку e, которая является различием t − a между нейроном ответом a и целевым вектором t. Правило обучения перцептронов learnp вычисляет желаемые изменения весов и смещений перцептрона, учитывая вектор входа p и связанную с ним ошибку e. Целевой вектор t должен содержать значения 0 или 1, потому что перцептроны (с hardlim передаточные функции) могут выводить только эти значения.
Каждый раз learnp выполняется, перцептрон имеет больше шансов получить правильные выходы. Доказано, что правило перцептрона сходится к решению в конечном числе итераций, если решение существует.
Если смещение не используется, learnp работает, чтобы найти решение путем изменения только вектора w веса, чтобы указать на входные векторы, которые будут классифицированы как 1 и удалены от векторов, которые будут классифицированы как 0. Это приводит к контуру принятия решения, которая перпендикулярна w и которая правильно классифицирует входные векторы.
Существует три условия, которые могут возникнуть для одного нейрона, когда представлен вектор входа p и вычисляется ответ сети a:
CASE 1. Если представлен вектор входа, и выход нейрона верен (a = t и e = t - a = 0), вектор веса w не меняется.
CASE 2. Если выход нейрона 0 и должен был быть 1 (a = 0 и t = 1, и e = t - a = 1)вектор входа p добавляется к вектору веса w. Это делает векторную точку веса ближе к вектору входа, увеличивая вероятность того, что вектор входа будет классифицирован как 1 в будущем.
ПРИМЕР 3. Если выход нейрона равен 1 и должен был быть 0 (a = 1 и t = 0, и e = t - a = -1)вектор входа p вычитается из вектора веса w. Это делает векторную точку веса более удаленной от вектора входа, увеличивая вероятность того, что вектор входа будет классифицирован как 0 в будущем.
Правило обучения перцептрон может быть написано более кратко с точки зрения ошибки e = t - a и изменения, которое должно быть внесено в вектор веса
CASE 1. Если e = 0, задайте значение, равное 0.
CASE 2. Если e = 1, то сделайте изменение И w равным pT.
ПРИМЕР 3. Если e = -1, то сделайте изменениеT.
Затем все три случая могут быть записаны с одним выражением:
Вы можете получить выражение для изменений смещения нейрона, отметив, что смещение является просто весом, который всегда имеет вход 1:
Для случая слоя нейронов у вас есть
и
Правило обучения перцептрон может быть обобщено следующим образом:
и
где e = t - a.
Теперь попробуйте простой пример. Начните с одного нейрона, имеющего входной вектор с двумя элементами.
net = perceptron; net = configure(net,[0;0],0);
Чтобы упростить ситуацию, установите смещение равным 0, а веса равными 1 и -0,8:
net.b{1} = [0];
w = [1 -0.8];
net.IW{1,1} = w;
Целевая пара входа задается как
p = [1; 2]; t = [1];
Вы можете вычислить выход и ошибку с
a = net(p)
a =
0
e = t-a
e =
1
и использовать функцию learnp для поиска изменения весов.
dw = learnp(w,p,[],[],[],[],e,[],[],[],[],[])
dw =
1 2
Затем новые веса получаются как
w = w + dw
w =
2.0000 1.2000
Процесс нахождения новых весов (и смещений) может повторяться до тех пор, пока нет ошибок. Напомним, что правило обучения перцептрон гарантированно сходится в конечном количестве шагов для всех задач, которые могут быть решены перцептроном. К ним относятся все классификационные задачи, которые линейно разделимы. Объекты, которые будут классифицированы в таких случаях, могут быть разделены одной линией.
Можно хотеть попробовать пример nnd4pr. Это позволяет вам выбрать новые входные векторы и применить правило обучения для их классификации.
Если sim и learnp неоднократно используются для представления входов перцептрону и для изменения весов и смещений перцептрона в соответствии с ошибкой, перцептрон в конечном счете найдет значения веса и смещения, которые решают проблему, учитывая, что перцептрон может решить ее. Каждый обход через все обучающие входные и целевые векторы называется проходом.
Функция train выполняет такой цикл вычисления. В каждом передайте функцию train переходит к заданной последовательности входов, вычисляя выходную, ошибочную и сетевую регулировку для каждого входного вектора в последовательности, когда представлены входы.
Обратите внимание, что train не гарантирует, что получившаяся сеть выполняет свою работу. Необходимо проверить новые значения W и b путем вычисления выхода для каждого входного вектора, чтобы увидеть, все ли цели достигнуты. Если сеть не выполняет успешно, можно обучить ее дальше, позвонив train снова с новыми весами и смещениями для большего количества обучающих проходов, или вы можете проанализировать задачу, чтобы увидеть, является ли она подходящей проблемой для перцептрона. Проблемы, которые не могут быть решены сетью перцептрона, обсуждаются в Ограничениях и Предостережениях.
Чтобы проиллюстрировать процедуру обучения, пройдите через простую задачу. Рассмотрим перцептрон с одним нейроном с одним векторным входом, имеющим два элемента:
Эта сеть и проблема, которую вы собираетесь рассмотреть, достаточно просты, чтобы вы могли проследить за тем, что делается с помощью вычислений рук, если хотите. Ниже следует проблема, описанная в [HDB1996].
Предположим, у вас есть следующая задача классификации и я хотел бы решить ее с одним векторным входом, двухэлементной сетью перцептрона.
Используйте начальные веса и смещение. Обозначите переменные на каждом шаге этого вычисления с помощью числа в круглых скобках после переменной. Таким образом, выше начальные значения являются W (0) и b (0).
Начните с вычисления выхода a перцептрона для первого входного вектора p1, используя начальные веса и смещение.
Выход a не равен целевому значению t 1, поэтому используйте правило перцептрона, чтобы найти инкрементальные изменения весов и смещений, основанные на ошибке.
Вычислить новые веса и смещение можно с помощью правил обновления перцептрона.
Теперь представьте следующий входной вектор, p2. Выход вычисляется ниже.
В этом случае цель равна 1, поэтому ошибка равна нулю. Таким образом, нет изменений в весах или смещении, поэтому W (2) = W (1) = [− 2 − 2] и b (2) = b (1) = − 1.
Можно продолжить таким образом, представив p3 далее, вычислив выход и ошибку, и внеся изменения в веса и смещение и т.д. Сделав один проход через все четыре входов, вы получите значения W (4) = [− 3 − 1] и b (4) = 0. Чтобы определить, получено ли удовлетворительное решение, сделайте один проход через все входные векторы, чтобы увидеть, производят ли они все желаемые целевые значения. Это не верно для четвертого входа, но алгоритм сходится на шестом представлении входа. Конечные значения:
W (6) = [− 2 − 3] и b (6) = 1.
На этом ручной расчет заканчивается. Теперь, как вы можете сделать это с помощью train функция?
Следующий код задает перцептрон.
net = perceptron;
Рассмотрим применение одного входа
p = [2; 2];
имеющий цель
t = [0];
Задайте epochs к 1, так что train проходит через входные векторы (здесь только один) всего один раз.
net.trainParam.epochs = 1; net = train(net,p,t);
Новые веса и смещение
w = net.iw{1,1}, b = net.b{1}
w =
-2 -2
b =
-1
Таким образом, начальные веса и смещение равны 0, и после обучения только на первом векторе они имеют значения [− 2 − 2] и − 1, так же как вы вычисляли вручную.
Теперь примените второй входной вектор p2. Выход равен 1, как это будет до тех пор, пока не изменятся веса и смещение, но теперь цель равна 1, ошибка будет 0, и изменение будет нулем. Можно продолжить таким образом, начиная с предыдущего результата и применяя новый входной вектор раз за разом. Но вы можете выполнить эту работу автоматически с train.
Обратиться train за одну эпоху один проход через последовательность всех четырех входных векторов. Начните с определения сети.
net = perceptron; net.trainParam.epochs = 1;
Входные векторы и целевые устройства
p = [[2;2] [1;-2] [-2;2] [-1;1]] t = [0 1 0 1]
Теперь обучите сеть с
net = train(net,p,t);
Новые веса и смещение
w = net.iw{1,1}, b = net.b{1}
w =
-3 -1
b =
0
Это тот же результат, что и раньше вручную.
Наконец, моделируйте обученную сеть для каждого из входов.
a = net(p)
a =
0 0 1 1
Выходы пока не равны целям, поэтому нужно обучать сеть не на один пасс. попробовать больше эпох. Это запуск дает среднюю абсолютную ошибку эффективности 0 после двух эпох:
net.trainParam.epochs = 1000; net = train(net,p,t);
Таким образом, сеть была обучена к моменту представления входов в третью эпоху. (Как известно из вычисления руки, сеть сходится на представлении шестого входного вектора. Это происходит в середине второй эпохи, но для обнаружения сходимости сети требуется третья эпоха.) Конечные веса и смещение
w = net.iw{1,1}, b = net.b{1}
w =
-2 -3
b =
1
Моделируемый выход и ошибки для различных входов
a = net(p)
a =
0 1 0 1
error = a-t
error =
0 0 0 0
Вы подтверждаете, что процедура обучения выполнена успешно. Сеть сходится и выдает правильные целевые выходы для четырех входных векторов.
Функция обучения по умолчанию для сетей, созданных с perceptron является trainc. (Вы можете найти это, выполнив net.trainFcn.) Эта функция обучения применяет правило обучения перцептронов в своей чистой форме, в том что отдельные входные векторы применяются индивидуально, последовательно, и коррекции весов и смещения производятся после каждого представления входного вектора. Таким образом, обучение перцептрона с train сходится в конечном количестве шагов, если представленная задача не может быть решена простым перцептроном.
Функция train может использоваться различными способами и другими сетями. Тип help train чтобы узнать больше об этой основной функции.
Можно хотеть попробовать различные примеры программ. Например, классификация с двумя-входным перцептроном иллюстрирует классификацию и обучение простого перцептрона.
Сети перцептрона должны быть обучены с adapt, который представляет входные векторы сети по одному и вносит коррекции в сеть по результатам каждой презентации. Использование adapt таким образом гарантирует, что любая линейно разделяемая задача решена в конечном количестве обучающих презентаций.
Как отмечалось на предыдущих страницах, перцептроны также могут быть обучены функцией train. Обычно, когда train используется для перцептронов, представляет входы сети пакетами и вносит коррекции в сеть на основе суммы всех индивидуальных коррекций. К сожалению, нет никаких доказательств того, что такой алгоритм настройки сходится для перцептронов. На этом основании использование train для перцептронов не рекомендуется.
Перцептронные сети имеют несколько ограничений. Во-первых, выходные значения перцептрона могут иметь только одно из двух значений (0 или 1) из-за жесткой предельной передаточной функции. Во-вторых, перцептроны могут классифицировать только линейно разделяемые наборы векторов. Если прямая линия или плоскость могут быть прорисованы, чтобы разделить входные векторы на их правильные категории, входные векторы являются линейно разделяемыми. Если векторы не являются линейно разделимыми, обучение никогда не достигнет точки, где все векторы классифицированы правильно. Однако было доказано, что, если векторы линейно разделимы, перцептроны, обученные адаптивно, всегда найдут решение за конечное время. Можно хотеть попробовать Линейно неотделимые векторы. Это показывает сложность попытки классифицировать входные векторы, которые не являются линейно разделимыми.
Однако справедливо отметить, что для решения более сложных задач могут использоваться сети с более чем одним перцептроном. Например, предположим, что у вас есть набор из четырех векторов, которые вы хотели бы классифицировать в отдельные группы, и что можно нарисовать две линии, чтобы разделить их. Сеть с двумя нейронами может быть найдена таким образом, что ее два контуров принятия решений классифицируют входы в четыре категории. Для дополнительной дискуссии о перцептронах и изучения более сложных проблем перцептрона, смотрите [HDB1996].
Длительное время обучения может быть вызвано наличием выходящего входного вектора, длина которого намного больше или меньше, чем другие входные векторы. Применение правила обучения перцептронов включает добавление и вычитание входных векторов из текущих весов и смещений в ответ на ошибку. Таким образом, вектор входа с большими элементами может привести к изменениям в весах и смещениях, которые требуют длительного времени, чтобы преодолеть намного меньший вектор входа. Можно хотеть попробовать Входные векторы Выбросов, чтобы увидеть, как выбросы влияют на обучение.
При незначительном изменении правила обучения перцептронов можно сделать время обучения нечувствительным к чрезвычайно большим или маленьким векторам выбросов входа.
Вот оригинальное правило обновления весов:
Как показано выше, чем больше вектор p входа, тем больше его влияние на вектор веса w. Таким образом, если вектор входа намного больше, чем другие векторы входа, то меньшие векторы входа должны быть представлены много раз, чтобы иметь эффект.
Решением является нормализация правила так, чтобы эффект каждого входного вектора на веса был одинаковой величины:
Нормированное правило перцептрона реализовано с функцией learnpn, который называется точно как learnp. Нормированная функция правила перцептрона learnpn требуется немного больше времени, чтобы выполнить, но значительно уменьшает количество эпох, если существуют выходящие входные векторы. Можно попробовать Нормализованное Правило Перцептрона, чтобы увидеть, как это нормализованное правило обучения работает.