Вот радиальная сеть базиса с R входами.
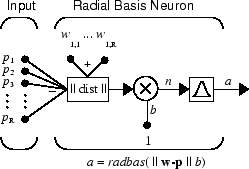
Заметьте, что выражение для чистого входа a radbas нейрон отличается от нейронов других. Здесь чистый вход в radbas передаточная функция - это векторное расстояние между его вектором веса w и входным вектором p, умноженное на b смещения. (The ||
dist
|| рамка на этом рисунке принимает входной вектор p и матрицу входного веса одной строки и создает скалярный продукт двух.)
Передаточная функция для радиального базиса нейронов
Вот график radbas передаточная функция.
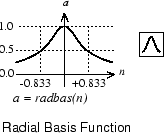
Радиальная функция базиса имеет максимум 1, когда ее вход равен 0. Когда расстояние между w и p уменьшается, выход увеличивается. Таким образом, радиальный базис нейрона действует как детектор, который производит 1 всякий раз, когда вход p идентичен его вектору w веса.
Смещение b позволяет чувствительность radbas нейрон, который будет скорректирован. Для примера, если бы нейрон имел смещение 0,1, он выводил бы 0,5 для любого вектора входа p на векторном расстоянии 8,326 (0 .8326/ b) из вектора веса w.
Радиальные сети базиса состоят из двух слоев: скрытого радиального слоя базиса S1 нейроны и выход линейный слой S2 нейроны.
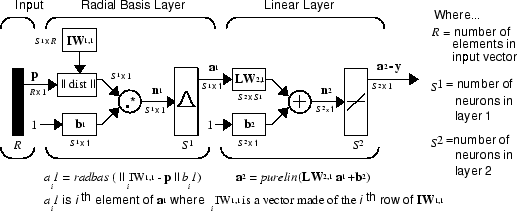
The ||
dist
|| прямоугольник на этом рисунке принимает входной вектор p и вход веса IW1,1, и создает вектор, имеющий S 1 элемента. Элементами являются расстояния между входным вектором и векторами i IW1,1 формируется из строк входа веса.
Вектор смещения b1 и выходы ||
dist
|| объединяются с MATLAB® операция. *, которая выполняет поэлементное умножение.
Выход первого слоя для сети прямого распространения net может быть получен со следующим кодом:
a{1} = radbas(netprod(dist(net.IW{1,1},p),net.b{1}))
К счастью, таких строк кода писать не придется. Все детали проектирования этой сети встроены в проекты newrbe и newrb, и вы можете получить их выходы с sim.
Можно понять, как ведет себя эта сеть, следуя вектору входа p через сеть в выход a2. Если вы представляете вектор входа в такой сети, каждый нейрон в радиальном слое базиса выдаст значение, согласно тому, насколько близок вектор входа к вектору веса каждого нейрона.
Таким образом, радиальные нейроны базиса с векторами веса, довольно отличающимися от входного вектора p, имеют выходы около нуля. Эти небольшие выходы оказывают незначительный эффект на линейные выходные нейроны.
В противоположность этому, радиальный базовый нейрон с вектором веса, близким к входному вектору p, производит значение около 1. Если нейрон имеет выход 1, его выходные веса во втором слое передают свои значения линейным нейронам во втором слое.
На самом деле, если бы только один радиальный базовый нейрон имел выход 1, а все другие имели выходы 0 с (или очень близкие к 0), выход линейного слоя был бы выходными весами активного нейрона. Однако это было бы крайним случаем. Как правило, несколько нейронов всегда в различной степени стреляют.
Теперь подробно рассмотрим, как работает первый слой. Взвешенный вход каждого нейрона является расстоянием между входным вектором и его вектором веса, вычисленным с dist. Чистый вход каждого нейрона является поэлементным продуктом его взвешенного входа с его смещением, вычисленным с netprod. Выход каждого нейрона является его чистым входом, прошедшим radbas. Если вектор веса нейрона равен входному вектору (транспонированному), его взвешенный вход равен 0, его чистый вход равен 0, а выход равен 1. Если вектор веса нейрона является расстоянием spread от входного вектора его взвешенный вход spread, его чистый вход является sqrt (− log (.5)) (или 0,8326), поэтому его выход равен 0,5.
Вы можете проектировать радиальные базисные сети с функцией newrbe. Эта функция может создать сеть с нулевой ошибкой на обучающих векторах. Вызывается следующим образом:
net = newrbe(P,T,SPREAD)
Функция newrbe принимает матрицы входа векторов P и целевые векторы Tи константа расширения SPREAD для радиального базового слоя и возвращает сеть с такими весами и смещениями, чтобы выходы были точно T когда входы P.
Эта функция newrbe создает столько же radbas нейроны, так как существуют входные векторы в P, и устанавливает веса первого слоя равными P'. Таким образом, существует слой radbas нейроны, в которых каждый нейрон действует как детектор для другого входного вектора. Если входных векторов Q, то будет Q нейронов.
Каждое смещение в первом слое установлено на 0 .8326/ SPREAD. Это дает радиальные функции базиса, которые пересекают 0,5 при взвешенных входах +/− SPREAD. Это определяет ширину области во входном пространстве, на которую реагирует каждый нейрон. Если SPREAD равен 4, затем каждый radbas нейрон ответит 0,5 или более на любые входные векторы в пределах векторного расстояния 4 от их вектора веса. SPREAD должен быть достаточно большим, чтобы нейроны сильно реагировали на перекрывающиеся области входного пространства.
Вес второго слоя IW 2,1 (или в коде, IW{2,1}) и смещения b2 (или в коде, b{2}) найдены путем симуляции выходов первого слоя a1 (A{1}), а затем решение следующего линейного выражения:
[W{2,1} b{2}] * [A{1}; ones(1,Q)] = T
Вы знаете входы во второй слой (A{1}) и цель (T), и слой линейный. Можно использовать следующий код, чтобы вычислить веса и смещения второго слоя, чтобы минимизировать суммарную квадратную ошибку.
Wb = T/[A{1}; ones(1,Q)]
Вот Wb содержит как веса, так и смещения с смещениями в последнем столбце. Суммарная квадратичная ошибка всегда равна 0, как объяснено ниже.
Существует проблема с C ограничениями (входные/целевые пары), и каждый нейрон имеет C + 1 переменных (веса C от
Cradbas нейроны и смещение). Линейная задача с C ограничениями и более чем C переменными имеет бесконечное число нулевых решений ошибок.
Таким образом, newrbe создает сеть с нулевой ошибкой для обучающих векторов. Единственное условие, необходимое для того, чтобы убедиться, что SPREAD достаточно большой, чтобы активные входные области radbas нейроны перекрываются достаточно, чтобы несколько radbas нейроны всегда имеют довольно большие выходы в любой заданный момент. Это делает сетевую функцию более гладкой и приводит к лучшему обобщению для новых входных векторов, происходящих между входными векторами, используемыми в проекте. (Однако SPREAD не должен быть настолько большим, чтобы каждый нейрон эффективно реагировал на одну и ту же большую площадь входного пространства.)
Недостаток newrbe это то, что она производит сеть с таким количеством скрытых нейронов, сколько существует входных векторов. По этой причине, newrbe не возвращает приемлемое решение, когда для правильного определения сети требуется много входных векторов, как это обычно бывает.
Функция newrb итеративно создает радиальную сеть базиса по одному нейрону за раз. Нейроны добавляются в сеть до тех пор, пока суммарно квадратная ошибка не упадет ниже цели ошибки или не будет достигнуто максимальное количество нейронов. Вызов этой функции:
net = newrb(P,T,GOAL,SPREAD)
Функция newrb принимает матрицы входа и целевых векторов P и T, и расчётные параметры GOAL и SPREAD, и возвращает нужную сеть.
Метод проекта newrb аналогично тому, как newrbe. Самое различие, что newrb создает нейроны по одному. При каждой итерации вектор входа, который приводит к снижению сетевой ошибки больше всего, используется для создания radbas нейрон. Ошибка новой сети проверяется, и если достаточно низко newrb завершено. В противном случае добавляется следующий нейрон. Эта процедура повторяется до тех пор, пока не будет достигнута цель ошибки или не будет достигнуто максимальное количество нейронов.
Как и в случае newrbe, важно, чтобы параметр spread был достаточно большим, чтобы radbas Нейроны реагируют на перекрывающиеся области входного пространства, но не настолько большие, чтобы все нейроны реагировали по существу одинаковым образом.
Почему не всегда используйте радиальную сеть базиса вместо стандартной сети прямого распространения? Радиальные сети базиса, даже если спроектированы эффективно с newrbe, имеют тенденцию иметь в разы больше нейронов, чем сопоставимая сеть прямого распространения с tansig или logsig нейроны в скрытом слое.
Это потому, что сигмоидные нейроны могут иметь выходы в большой области входного пространства, в то время как radbas нейроны реагируют только на относительно небольшие области входного пространства. Результатом является то, что чем больше входное пространство (с точки зрения количества входов и областей значений, в которых эти входы изменяются), тем больше radbas требуются нейроны.
С другой стороны, разработка радиального базисный сети часто занимает гораздо меньше времени, чем обучение сигмоидной/линейной сети, и иногда может привести к использованию меньшего количества нейронов, как видно из следующего примера.
Пример Радиальное приближение базиса показывает, как радиальная сеть базиса используется, чтобы соответствовать функции. Здесь проблема решается всего пятью нейронами.
Примеры Радиальный базис Подстилающих Нейронов и Радиальный Базис Перекрывающих Нейронов исследуют, как константа распространения влияет на процесс проекта радиальных базовых сетей.
В Radial Basis Underlapping Neuron радиальная сеть базиса предназначена для решения той же задачи, что и в Радиальном приближении базиса. Однако на этот раз используемая константа распределения составляет 0,01. Таким образом, каждый радиальный нейрон базиса возвращает 0,5 или ниже для любого вектора входа с расстоянием 0,01 или более от его вектора веса.
Поскольку обучающие входы происходят с интервалами 0,1, никакие два радиальных базиса нейронов не имеют сильного выхода для любого данного входа.
Радиальный базис Подстилающих Нейронов показал, что наличие слишком маленькой константы расширения может привести к решению, которое не обобщается из входных/целевых векторов, используемых в проекте. Пример перекрытия радиального базиса нейронов показывает обратную задачу. Если константа распространения достаточно велика, нейроны радиального базиса выдадут большие значения (около 1,0) для всех входов, используемых для проектирования сети.
Если все радиальные нейроны базиса всегда выводят 1, любая информация, представленная в сеть, теряется. Независимо от того, какой вход, второй слой выводит 1. Функция newrb будет пытаться найти сеть, но не может из-за числовых проблем, возникающих в этой ситуации.
Мораль истории состоит в том, что выберите константу расширения, большую, чем расстояние между соседними входными векторами, чтобы получить хорошее обобщение, но меньше, чем расстояние через все входное пространство.
Для этой задачи, которая означала бы выбор постоянной распределения, большей, чем 0,1, интервала между входами и меньшей, чем 2, расстояния между крайним левым и крайним правым входами.