Вычислите полиномиальные коэффициенты, которые наилучшим образом соответствуют входным данным в смысле наименьших квадратов
Математические функции/полиномиальные функции
dsppolyfun
Блок методом аппроксимации методом наименьших квадратов вычисляет коэффициенты полинома n-го порядка, который лучше всего подходит для входных данных в смысле наименьших квадратов, где вы задаете n в параметре Polynomial order. Отдельный набор коэффициентов n + 1 вычисляется для каждого столбца M -by N входа, u.
Для данного входного столбца блок вычисляет набор коэффициентов, c1, c2,..., cn+1, который минимизирует величину
где ui - i-й элемент во входном столбце, и
Значения независимой переменной, x1, x2..., xM, определены как длина - M вектор Control points параметром. Те же M управляющие точки используются для всех N аппроксимаций полиномом и могут быть равномерно или неравномерно разнесены. Эквивалентный MATLAB® код показан ниже.
c = polyfit(x,u,n) % Equivalent MATLAB code
Для удобства блок обрабатывает длинно- M неориентированный векторный вход как M-на-1 матрицу.
Каждый столбец выходной матрицы (n + 1) -by N, c, представляет набор коэффициентов n + 1, описывающих полином наилучшего соответствия для соответствующего столбца входов. Коэффициенты в каждом столбце расположены в порядке убывания экспонентов, c1, c2,..., cn+1.
В модели ex_leastsquarespolyfit_ref ниже блок Polynomial Evaluation использует полином второго порядка
сгенерировать четыре значения зависимой переменной y из четырех значений независимой переменной u, полученных в верхнем порте. Полиномиальные коэффициенты подаются в вектор [-2 0 3] в нижнем порте. Обратите внимание, что коэффициент члена первого порядка равен нулю.
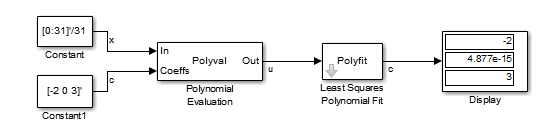
Параметр Control points блока Last Squares Polynomial Fit сконфигурирован с теми же четырьмя значениями независимых переменных u, которые используются в качестве входа в блок Polynomial Evaluation, [1 2 3 4]. Блок Аппроксимация полиномом методом наименьших квадратов использует эти значения вместе с входом значениями зависимых переменных y, чтобы восстановить исходные полиномиальные коэффициенты.
Значения независимой переменной, которой соответствуют данные в каждом входном столбце. Для входного параметра M -by N этот параметр должен быть вектором с M длиной. Настраиваемый (Simulink).
Порядок, n, полинома, используемого при построении наилучшей подгонки. Количество коэффициентов n + 1.
Плавающая точка двойной точности
Плавающая точка с одной точностью
| Detrend | DSP System Toolbox |
| Полиномиальная оценка | DSP System Toolbox |
| Тест полиномиальной устойчивости | DSP System Toolbox |
polyfit | MATLAB |