Для многих автономных систем знание состояния системы является необходимым условием для разработки любых приложений. В действительности, однако, состояние часто не получается непосредственно. Состояние системы обычно выводится или оценивается на основе выходов системы, измеренных определенными инструментами (такими как датчики), и потока состояния, управляемого динамической моделью или моделью движения. Некоторые простые методы, такие как оценка методом наименьших квадратов или пакетная оценка, достаточны для решения статических или автономных задач оценки. Для задач оценки в режиме онлайн и в реальном времени (последовательных) обычно применяются более сложные фильтры оценки.
Система оценки состоит из динамической модели или модели движения, которая описывает поток состояния и модели измерения, которая описывает, как получаются измерения. Математически эти две модели могут быть представлены уравнением движения и уравнением измерения. Для примера уравнение движения и уравнение измерения для общей нелинейной дискретной системы оценки может быть записано как:
где k - временной шаг, <reservedrangesplaceholder10> <reservedrangesplaceholder9> системное состояние во временном шаге k, f (x k) государственно-зависимое уравнение движения, h (x k) государственное зависимое уравнение измерения, и <reservedrangesplaceholder1> <reservedrangesplaceholder0> - выход.
В большинстве случаев создание идеальной модели для захвата всего динамического явления невозможно. Например, включение всех трений в модель движения автономного транспортного средства невозможно. Чтобы компенсировать эту немоделированную динамику, технологический шум (w) часто добавляется к динамической модели. Кроме того, когда измерения проводятся, многочисленные источники ошибок, такие как калибровочные ошибки, неизбежно включаются в измерения. Чтобы учесть эти ошибки, к модели измерения должен быть добавлен правильный шум измерения. Система оценки, включающая эти случайные шумы и ошибки, называется системой стохастической оценки, которая может быть представлена:
где w k и v k представляют шум процесса и шум измерения, соответственно.
Для большинства инженерных приложений шум процесса и шум измерения приняты, чтобы следовать нулевому среднему Гауссову или нормальному распределениям, или, по крайней мере, аппроксимируются Гауссовыми распределениями. Кроме того, поскольку точное состояние неизвестно, оценка состояния является случайной переменной, обычно принимаемой для следования Гауссовым распределениям. Предположение, что Гауссовы распределения для этих переменных значительно упрощают проект оценочного фильтра и формируют базис семейства фильтров Калмана.
Гауссовское распределение для случайной переменной (<reservedrangesplaceholder8>) параметризовано средним значением μ и ковариационная матрица P, который написан как <reservedrangesplaceholder5> <reservedrangesplaceholder4> (μ, P). Учитывая Гауссово распределение, среднее, которое также является наиболее вероятным значением x, определяется ожиданием (E) как:
Среднее значение также называется первым моментом x о источнике. Ковариация, которая описывает неопределенность x, определяется ожиданием (E) как:
Ковариацию также называют вторым моментом x о ее среднем значении.
Если размерность x равна единице, P является только скаляром. В этом случае значение P обычно обозначается σ2 и называется отклонением. Квадратный корень, σ, называется стандартным отклонением x. Стандартное отклонение имеет важный физический смысл. Например, следующий рисунок показывает функцию плотности вероятностей (которая описывает вероятность того, что x принимает определенное значение) для одномерного Гауссова распределения со средним равным μ и стандартным отклонением, равным σ. Приблизительно 68% данных находятся в пределах 1 σ контура x, 95% данных находятся в пределах 2 σ контуров, и 99,7% данных находится в пределах 3 σ контуров.
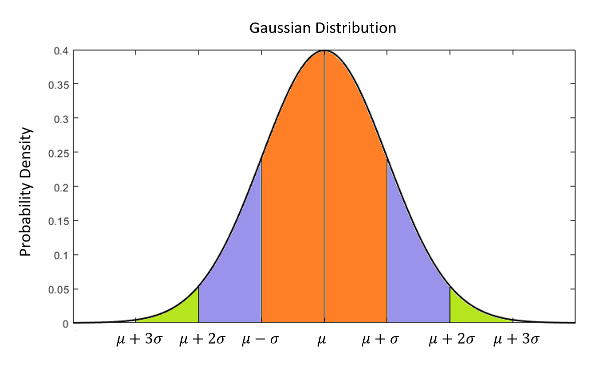
Несмотря на то, что предположение Гауссова распределения является доминирующим предположением в инженерных приложениях, существуют системы, состояние которых не может быть аппроксимировано Гауссовыми распределениями. В этом случае для точной оценки состояния системы требуются Нефильтры Калмана (такие как фильтр частиц).
Цель разработки фильтра состоит в том, чтобы оценить состояние системы с помощью измерений и динамики системы. Поскольку измерения обычно проводятся в дискретных временных шагах, процесс фильтрации обычно разделяется на два шага:
Предсказание: Распространите состояние и ковариацию между дискретными временными шагами измерения (k = 1, 2, 3,..., N) с помощью динамических моделей. Этот шаг также называется обновлением потока.
Коррекция: Исправление оценки состояния и ковариации на дискретных временных шагах с помощью измерений. Этот шаг также называется обновлением измерения.
Для представления государственной оценки и статуса ковариации на различных этапах, <reservedrangesplaceholder14> <reservedrangesplaceholder13> | k и <reservedrangesplaceholder11> <reservedrangesplaceholder10> | k обозначают государственную оценку и ковариацию после коррекции во временном шаге k, тогда как <reservedrangesplaceholder7> <reservedrangesplaceholder6> +1 | k и <reservedrangesplaceholder4> <reservedrangesplaceholder3> +1 | k обозначает государственную оценку и ковариацию, предсказанную от предыдущего временного шага k к шагу <reservedrangesplaceholder0> +1 текущего времени.
На этапе предсказания распространение состояния является простым. Фильтр должен только заменить оценку состояния в динамическую модель и распространить ее вперед во времени как x k + 1 | k = f (x k | k).
Ковариационное распространение сложнее. Если система оценки линейна, то ковариация может быть распространена (P k | k − P k + 1 | k) точно в стандартном уравнении, основанном на свойствах системы. Для нелинейных систем точное ковариационное распространение является сложным. Основное различие между различными фильтрами заключается в том, как они распространяют ковариацию системы. Для примера:
Линейный фильтр Калмана использует линейное уравнение, чтобы точно распространить ковариацию.
Расширенный фильтр Калмана распространяет ковариацию на основе линейного приближения, что делает большие ошибки, когда система сильно нелинейна.
Сигма-точечный фильтр Калмана использует неароматизированное преобразование, чтобы отсчитать ковариационное распределение и распространить его во времени.
То, как распространяются состояние и ковариация, также сильно влияет на сложность расчетов фильтра. Для примера:
Линейный фильтр Калмана использует линейное уравнение, чтобы точно распространить ковариацию, которая обычно является вычислительно эффективной.
Расширенный фильтр Калмана использует линейные приближения, которые требуют вычисления якобиевых матриц и требуют более расчета ресурсов.
Для сигма-точечного фильтра Калмана необходима выборка распределения ковариации и, следовательно, требуется распространение нескольких точек выборки, что дорого для высокомерных систем.
На этапе коррекции фильтр использует измерения, чтобы исправить оценку состояния через обратную связь измерения. В основном, различие между истинным измерением и предсказанным измерением складывается в оценку состояния после того, как она умножается на матрицу усиления с обратной связью. Для примера в расширенном фильтре Калмана коррекция для оценки состояния определяется:
Как уже упоминалось, x k + 1 | k является оценкой состояния до (априори) коррекции и x k + 1 | k + 1 является оценкой состояния после (апостериори) коррекции. K k является усилением Калмана, управляемым оптимальным критерием, y k является истинным измерением, а h (x k + 1 | k) является предсказанным измерением.
На этапе коррекции фильтр также корректирует ковариацию оценочной ошибки. Основной идеей является исправление вероятностного распределения x с помощью информации о распределении y k+1. Это называется апостериорной плотностью вероятностей x заданных y. В фильтре шаги предсказания и коррекции обрабатываются рекурсивно. Блок-схема показывает общие алгоритмы для фильтров Калмана .
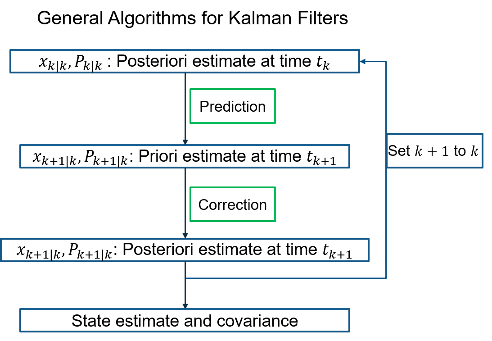
Sensor Fusion and Tracking Toolbox™ предлагает несколько оценочных фильтров, которые можно использовать для оценки и отслеживания состояния динамической системы.
Классический фильтр Калмана (trackingKF) - оптимальный фильтр для линейных систем с Гауссовым процессом и измерительным шумом. Линейная система оценки может быть задана как:
И процесс, и шум измерения приняты Гауссовыми, то есть:
Поэтому ковариационная матрица может быть непосредственно распространена между шагами измерения, используя линейное алгебраическое уравнение как:
Корректирующие уравнения для обновления измерения:
Чтобы вычислить матрицу усиления Калмана (K k) в каждом обновлении, фильтр должен вычислить обратную матрицу:
Поскольку размерность инвертированной матрицы равна размерности предполагаемого состояния, это вычисление требует некоторых вычислительных усилий для высокомерной системы. Для получения дополнительной информации см. «Линейные фильтры Калмана».
Альфа-бета-фильтр (trackingABF) - неоптимальный фильтр, применяемый к линейным системам. Фильтр можно рассматривать как упрощенный фильтр Калмана. В фильтре Калмана усиление Калмана и ковариационные матрицы вычисляются динамически и обновляются на каждом шаге. Однако в альфа-бета-фильтре эти матрицы являются постоянными. Эта обработка жертвует оптимальностью фильтра Калмана, но улучшает эффективность расчета. По этой причине альфа-бета фильтр может быть предпочтительным, когда ресурсы расчета ограничены.
Самый популярный расширенный фильтр Калмана (trackingEKF) изменяется из классического фильтра Калмана, чтобы адаптироваться к нелинейным моделям. Он работает путем линеаризации нелинейной системы о оценке состояния и пренебрежения нелинейными терминами второго и более высокого порядка. Его формулировки - в основном то же как те из линейного Фильтра Калмана за исключением того, что <reservedrangesplaceholder8> <reservedrangesplaceholder7> и матрицы <reservedrangesplaceholder6> k в Фильтре Калмана заменены якобиевскими матрицами f (x k) и h (x k):
Если истинная динамика системы оценок близка к линеаризированной динамике, то использование этого линейного приближения не приводит к значительным ошибкам в течение короткого периода времени. По этой причине EKF может создать относительно точные оценки состояния для мягко нелинейной системы оценки с короткими интервалами обновления. Однако, поскольку EKF пренебрегает терминами более высокого порядка, он может различаться для сильно нелинейных систем (квадроторы, для примера), особенно с большими интервалами обновления.
По сравнению с KF, EKF должен вывести матрицы Якобия, что требует, чтобы динамика системы была дифференцируемой, и вычислить матрицы Якобия, чтобы линеаризировать систему, которая требует больше вычислительных активов.
Обратите внимание, что для систем оценки с состоянием, выраженным в сферических координатах, можно использовать trackingMSCEKF.
Сигма-точечный фильтр Калмана (trackingUKF) использует нескромное преобразование (UT), чтобы приблизительно распространить ковариационное распределение для нелинейной модели. Подход UT дискретизирует ковариационное Гауссово распределение в текущем времени, распространяет точки выборки (называемые сигма-точками) с помощью нелинейной модели и аппроксимирует полученное ковариационное распределение, принятое как Гауссово, путем оценки этих распространенных сигма-точек. Рисунок иллюстрирует различие между фактическим распространением, линеаризированным распространением и UT распространением ковариации неопределенности.
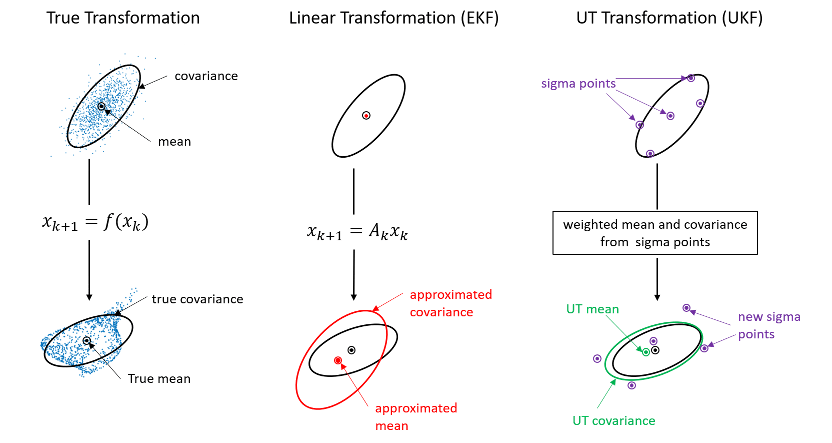
По сравнению с подходом линеаризации, принятым EKF, UT-подход приводит к более точному распространению ковариации и приводит к более точной оценке состояния, особенно для сильно нелинейных систем. UKF не требует деривации и вычисления якобиевых матриц. Однако UKF требует распространения 2 n + 1 сигмы точек через нелинейную модель, где n является размерностью предполагаемого состояния. Это может быть в вычислительном отношении дорогим для высокомерных систем.
Кубатурный фильтр Калмана (trackingCKF) использует несколько иной подход, чем UKF, чтобы сгенерировать 2 n выборочные точки, используемые для распространения распределения ковариации, где n является размерностью предполагаемого состояния. Этот альтернативный набор точек выборки часто приводит к лучшей статистической устойчивости и избегает расхождения, которое может возникнуть в UKF, особенно при запуске в платформе с одной точностью. Обратите внимание, что CKF по существу эквивалентна UKF, когда параметры UKF установлены на α = 1, β = 0 и κ = 0. См. trackingUKF для определения этих параметров.
Фильтр Гауссова - Суммы (trackingGSF) использует взвешенную сумму нескольких Гауссовых распределений, чтобы аппроксимировать распределение предполагаемого состояния. Предполагаемое состояние задается взвешенной суммой гауссовских состояний:
где N - количество Гауссовых состояний, поддерживаемых в фильтре, и c ki - вес для соответствующего Гауссова состояния, который изменяется в каждом обновлении на основе измерений. Множественные Гауссовы состояния следуют той же динамической модели, что и:
Фильтр эффективен при оценке состояний не полностью наблюдаемой системы оценки. Для примера фильтр может использовать несколько параметризованных под углом расширенных фильтров Калмана, чтобы оценить состояние системы, когда доступны только измерения области значений. Смотрите Отслеживание с измерениями только для диапазона для примера.
Интерактивный фильтр нескольких моделей (trackingIMM) использует несколько Гауссовых фильтров, чтобы отследить положение цели. В высоко маневрируемых системах динамика системы может переключаться между несколькими моделями (постоянная скорость, постоянное ускорение и постоянный поворот для примера). Моделировать движение цели, используя только одну модель движения, трудно. Система оценки нескольких моделей может быть описана как:
где i = 1, 2,..., M, и M - общее количество динамических моделей. Фильтр IMM разрешает неопределенность движения цели, используя несколько моделей для маневрирующей цели. Фильтр обрабатывает все модели одновременно и представляет общую оценку как взвешенную сумму оценок из этих моделей, где веса являются вероятностью каждой модели. См. пример Отслеживания Маневрирующих Целей.
Фильтр частиц (trackingPF) отличается от семейства фильтров Калмана (EKF и UKF, для примера), так как не полагается на предположение Гауссова распределения, которое соответствует параметрическому описанию неопределенностей с использованием среднего и отклонения. Вместо этого фильтр частиц создает несколько симуляций взвешенных выборок (частиц) операции системы через время, а затем анализирует эти частицы как прокси для неизвестного истинного распределения. Краткое введение алгоритма фильтра частиц показано на рисунке.
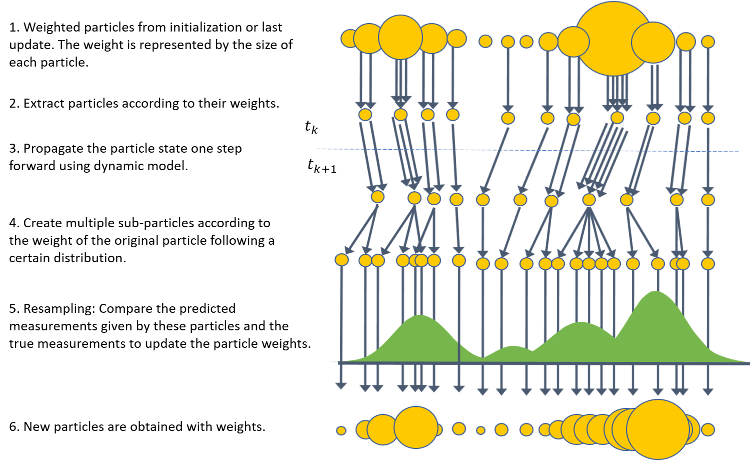
Мотивация этого подхода является аргументом закона больших чисел - когда количество частиц становится большим, их эмпирическое распределение приближается к истинному распределению. Основным преимуществом фильтра частиц по сравнению с различными фильтрами Калмана является то, что он может быть применен к негауссовым распределениям. Кроме того, фильтр не имеет ограничений на динамику системы и может использоваться с сильно нелинейной системой. Другим преимуществом является присущая фильтру способность представлять несколько гипотез о текущем состоянии. Поскольку каждая частица представляет гипотезу о состоянии с определенной ассоциированной вероятностью, фильтр частиц полезен в случаях, когда существует неоднозначность относительно состояния.
Наряду с этими привлекательными свойствами является высокая вычислительная сложность фильтра частиц. Для примера UKF требует распространения 13 точек выборки, чтобы оценить 3-D положение и скорость объекта. Однако фильтру частиц могут потребоваться тысячи частиц для получения разумной оценки. Кроме того, количество частиц, необходимых для достижения хорошей оценки, растет очень быстро с размерностью состояния и может привести к проблемам депривации частиц в высоко размерных пространствах. Поэтому фильтры частиц в основном применялись к системам с достаточно низким количеством размерностей (для примера роботов).
В следующей таблице перечислены все фильтры отслеживания, доступные в Sensor Fusion and Tracking Toolbox, и как выбрать их, заданные ограничения на нелинейность системы, распределение состояний и вычислительную сложность.
| Имя фильтра | Поддерживает нелинейные модели | Гауссовское государство | Вычислительная сложность | Комментарии |
| Альфа-Бета | Низко | Субоптимальный фильтр. | ||
| Кальман | ✓ | Средний Низкий | Оптимально для линейных систем. | |
| Расширенный Калман | ✓ | ✓ | Среда | Использует линеаризированные модели для распространения ковариации неопределенности. |
| Неароматизированный Калман | ✓ | ✓ | Средний Высокий | Дискретизирует ковариацию неопределенности, чтобы распространить точки выборки. Может стать численно нестабильным в платформе с одной точностью. |
| Кубатурный Калман | ✓ | ✓ | Средний Высокий | Дискретизирует ковариацию неопределенности, чтобы распространить точки выборки. Численно стабильный. |
| Гауссов-Сум | ✓ | ✓ (Принимает взвешенную сумму распределений) | Высоко | Хорошо для частично наблюдаемых случаев (отслеживание только угла для примера). |
| Взаимодействие нескольких моделей (IMM) | ✓ Несколько моделей | ✓ (Принимает взвешенную сумму распределений) | Высоко | Маневрирующие объекты (которые ускоряются или поворачиваются, например) |
| Частица | ✓ | Очень Высокий | Дискретизирует распределение неопределенности с использованием взвешенных частиц. |
[1] Wang, E.A., and R. Van Der Merwe. Неароматизированный сигма-точечный фильтр Калмана для нелинейной оценки. IEEE 2000 Адаптивные системы для обработки сигналов, связи и симпозиума по управлению. № 00EX373, 2000, стр 153–158.
[2] Фан, Х., Н. Тянь, Я. Ван, М. Чжоу и М. А. Хейл. Нелинейная байесовская оценка: от фильтрации Калмана до более широкого горизонта. IEEE/CAA Journal of Automatica Sinica. Том 5, № 2, 2018, с. 401-417.
[3] Арасаратнам, И. и С. Хайкин. Кубатурные фильтры Калмана. Транзакции IEEE по автоматическому управлению. Том 54, № 6, 2009, стр. 1254-1269.
[4] Конатовский, С., П. Каневский, и Я. Матушевский. «Сравнение точности оценки фильтров EKF, UKF и PF». Ежегодная навигация. Том 23, № 1, 2016, с. 69-87.
[5] Darko, J. «Object Tracking: Фильтр частиц with Ease». https://www.codeproject.com/Articles/865934/Object-Tracking-Particle-Filter-with-Ease.