Когда количество входов в нечеткую систему увеличивается, количество правил увеличивается экспоненциально. Эта большая основа правил снижает вычислительную эффективность нечеткой системы. Это также затрудняет операцию нечеткой системы, и это затрудняет настройку параметров функции правила и членства. Поскольку многие приложения имеют ограниченный объем обучающих данных, большая основа правил уменьшает обобщаемость настроенных нечетких систем.
Чтобы преодолеть эту проблему, можно реализовать систему нечеткого вывода (FIS) как дерево меньших взаимосвязанных объектов FIS, а не как один монолитный объект FIS. Эти fuzzy trees также известны как hierarchical fuzzy systems, потому что нечеткие системы расположены в иерархических древовидных структурах. В древовидной структуре выходы низкоуровневых нечетких систем используются в качестве входов для высокоуровневых нечетких систем. Нечеткое дерево более эффективно в вычислительном отношении и легче понять, чем одно FIS с таким же количеством входов.
Существует несколько нечетких древовидных структур, которые можно использовать для вашего приложения. На следующем рисунке показаны обычно используемые нечеткие древовидные структуры: инкрементальная, агрегированная или каскадная структура.
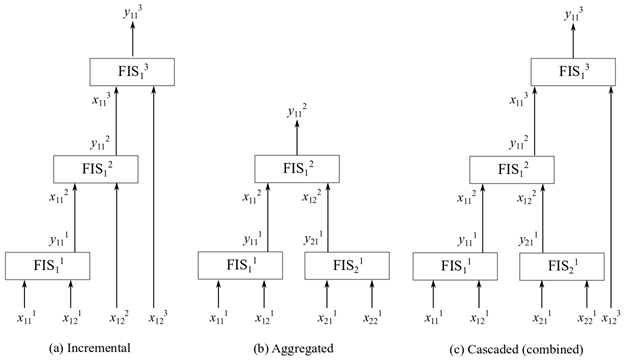
В инкрементальной структуре входные значения включаются в несколько этапов, чтобы уточнить выходные значения на нескольких уровнях. Для примера предыдущий рисунок показывает трехуровневое инкрементальное нечеткое дерево, имеющее системы нечеткого вывода , где i указывает индекс FIS на n-м уровне. В инкрементальном нечетком дереве i = 1, что означает, что каждый уровень имеет только одну систему нечеткого вывода. На предыдущем рисунке j-й вход i-го FIS на n-м уровне показан как вход, тогда как k-й выход i-го FIS на n-м уровне показан как вход. На рисунке n = 3, j = 1 или 2 и k = 1. Если каждый вход имеет m функции принадлежности (MF), то каждый FIS имеет полный набор m2 правила. Следовательно, общее количество правил nm2 = 3 ⨉ 32 = 27.
Следующий рисунок показывает монолитный (n = 1) FIS с четырьмя входами (j = 1, 2, 3, 4) и тремя MF (m = 3 ).
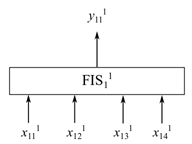
В FIS этого рисунка общее количество правил nm4 = 1 ⨉ 34 = 81. Следовательно, общее количество правил в инкрементном нечетком дереве линейно с количеством входа пар.
Вход параметров на разных уровнях в инкрементном нечетком дереве использует входные рейтинги на основе их вкладов в конечные выходные значения. Значения входа, которые вносят наибольший вклад, обычно используются на самом низком уровне, в то время как наименее влиятельные таковые используются на самом высоком уровне. Другими словами, входные значения низкого ранга зависят от входных значений высокого ранга.
В инкрементальном нечетком дереве каждое входное значение обычно вносит вклад в процесс вывода в определенной степени, не будучи значительно коррелированным с другими входами. Например, нечеткая система прогнозирует возможность покупки автомобиля с помощью четырёх входов: цвет, количество дверей, степень лошади и автопилот. Входы являются четырьмя различными автомобильными функциями, которые могут независимо влиять на решение покупателя. Следовательно, входы могут быть ранжированы с помощью существующих данных для создания нечеткого дерева, как показано на следующем рисунке.
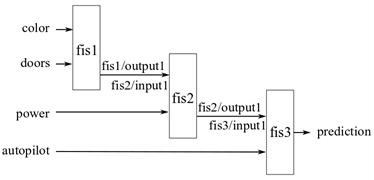
Для примера, который иллюстрирует создание инкрементного нечеткого дерева в MATLAB®, см. пример «Создание инкрементного дерева FIS» на fistree страница с описанием.
В агрегированной структуре входные значения включаются как группы на самом низком уровне, где каждая входная группа подается в FIS. Выходы нечетких систем нижнего уровня объединяются (агрегируются) с помощью нечетких систем более высокого уровня. Для примера в следующих показах двухуровневое агрегированное нечеткое дерево, имеющее системы нечеткого вывода , где in указывает индекс FIS на n-м уровне .
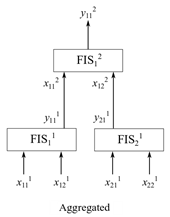
В этом агрегированном нечетком дереве i 1 = 1,2 и i 2 = 1. Следовательно, каждый уровень включает в себя разное количество FIS. j-й вход in-го FIS показан на рисунке как вход, и k-й выход in-го FIS показан как выход. На рисунке j = 1,2 и k = 1. Другими словами, каждая FIS имеет два входа и один выход. Если каждый вход имеет m MF, то каждый FIS имеет полный набор m2 правила. Следовательно, общее количество правил для трех нечетких систем составляет 3 м2 = 3 ⨉ 32 = 27, что является тем же самым, что и инкрементальная FIS для аналогичного строения.
В агрегированном нечетком дереве входные значения естественно сгруппированы вместе для принятия конкретных решений. Например, автономная задача навигации робота сочетает в себе предотвращение препятствий и достижение цели подзадачи для навигации без столкновения. Для достижения задачи навигации нечеткое дерево может использовать четыре входов: расстояние до ближайшего препятствия, угол ближайшего препятствия, расстояние до цели и угол цели. Расстояния и углы измеряются относительно текущего положения и направления курса робота. В этом случае на самом низком уровне входы естественно сгруппированы, как показано на следующем рисунке: расстояние препятствия и угол препятствия (группа 1) и расстояние цели и угол цели (группа 2). Две нечеткие системы отдельно обрабатывают входы отдельных групп, а затем другая нечеткая система объединяет их выходы, чтобы получить свободный от столкновения курс для робота.
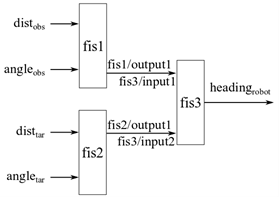
Для примера, который иллюстрирует создание агрегированного нечеткого дерева в MATLAB, смотрите пример Создать агрегированное дерево FIS на fistree страница с описанием.
В изменении агрегированной структуры, известной как parallel structure
[1], выходы нечетких систем самого низкого уровня непосредственно суммируются, чтобы сгенерировать окончательное выходное значение. Следующий рисунок показывает пример параллельного нечеткого дерева, где выводит fis1 и fis2 суммируются для получения конечного выхода.
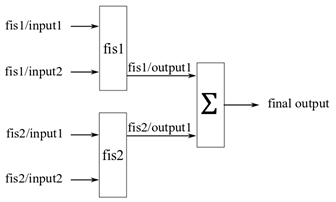
The fistree объект не предоставляет узел суммирования Поэтому необходимо добавить пользовательский метод агрегации, чтобы вычислить параллельное нечеткое дерево. Например, смотрите пример «Создание и оценка параллельного дерева FIS» на fistree страница с описанием.
Каскадная структура, также известная как комбинированная структура, объединяет как инкрементальные, так и агрегированные структуры для создания нечеткого дерева. Эта структура подходит для системы, которая включает как коррелированные, так и некоррелированные входы. Дерево группирует коррелированные входы в агрегированной структуре и добавляет некоррелированные входы в инкрементальную структуру. Следующий рисунок показывает пример каскадной древовидной структуры, где первые четыре входных параметра сгруппированы попарно в агрегированной структуре, а пятый вход добавлен в пошаговой структуре.
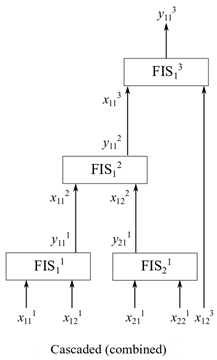
Для примера рассмотрим задачу навигации робота, обсуждаемую в Aggregated Structure. Предположим, что задача включает другой вход, предыдущий курс робота, принятый во внимание, чтобы предотвратить большие изменения в курсе робота. Можно добавить этот вход с помощью инкрементальной структуры следующей схемы.
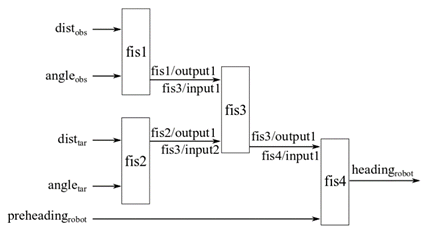
Для примера, который иллюстрирует создание агрегированного нечеткого дерева в MATLAB, смотрите пример «Создать каскадное дерево FIS» на fistree страница с описанием.
Когда вы оцениваете fistree объект возвращает результаты только для открытых выходов, которые не соединены с никакими входами FIS в нечетком дереве. Вы можете получить доступ к другим выходам в дереве. Например, в следующей схеме агрегированного нечеткого дерева, можно хотеть получить выход fis2 при вычислении дерева.
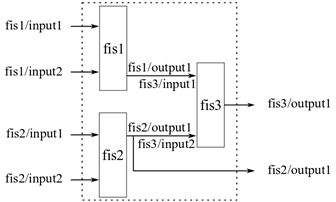
Можно добавить такие выходы к fistree объект. Можно также удалить выходы условии, что нечеткое дерево всегда имеет по крайней мере один выход. Например, смотрите пример «Update FIS Tree Outputs» на fistree страница с описанием.
A fistree объект позволяет использовать одно и то же значение для нескольких входов. Для образца на следующем рисунке input2 от fis1 и input1 от fis2 используйте то же значение во время оценки.
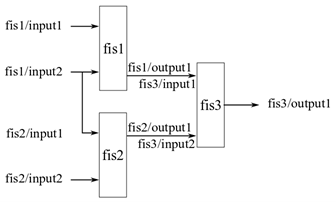
Для примера, показывающего, как создать дерево FIS таким образом, смотрите пример «Используйте то же значение для нескольких входов дерева FIS» на fistree страница с описанием.
Можно добавить или удалить отдельные элементы FIS из fistree объект. Когда вы делаете это, программное обеспечение автоматически обновляет Connections, Inputs, и Outputs свойства fistree объект. Например, смотрите пример «Обновление систем нечеткого вывода в дереве FIS» на fistree страница с описанием.
После того, как вы сконфигурировали внутренние соединения в вашем нечетком дереве, следующий шаг - настроить параметры дерева. Для получения примера смотрите Tune FIS Tree for Gas Mileage Предсказания.
[1] Siddique, Nazmul, and Hojjat Adeli. Вычислительный интеллект: синергии нечеткой логики, нейронных сетей и эволюционных вычислений. Оксфорд, Великобритания: John Wiley & Sons Ltd, 2013. https://doi.org/10.1002/9781118534823.