В последние годы число и разнообразие применений нечеткой логики значительно увеличилось. Приложения варьируются от потребительских продуктов, таких как камеры, видеокамеры, стиральные машины и микроволновые печи, до управления промышленными процессами, медицинского инструментирования, систем поддержки принятия решений и выбора портфеля.
Чтобы понять, почему выросло использование нечеткой логики, необходимо сначала понять, что подразумевается под нечеткой логикой.
Нечеткая логика имеет два разных значения. В узком смысле нечеткая логика является логической системой, которая является расширением многозначной логики. Однако в более широком смысле нечеткая логика (FL) является почти синонимом теории нечетких множеств, теории, которая относится к классам объектов без четких четко определенных контуров. В таких случаях членство в наборе является вопросом степени. В этой перспективе нечеткая логика в её узком смысле является ветвью FL. Даже по более узкому определению нечеткая логика отличается как концепцией, так и субстанцией от традиционных многозначных логических систем.
В программном обеспечении Fuzzy Logic Toolbox™ нечеткая логика должна интерпретироваться как FL, то есть нечеткая логика в её широком смысле. Основные идеи, лежащие в основе FL, объясняются в Foundations of Fuzzy Logic. Можно добавить, что базовое понятие, лежащее в основе FL, является концепцией лингвистической переменной, то есть переменной, значения которой являются словами, а не числами. В эффект большая часть FL может рассматриваться как методология вычисления словами, а не числами. Хотя слова по своей сути менее точны, чем числа, их использование ближе к человеческой интуиции. Кроме того, вычисление словами использует допуск к неточности и тем самым снижает стоимость решения.
Другая базовая концепция в FL, которое играет центральную роль в большинстве его приложений, - это понятие нечеткого правила, если-то или, просто, нечеткого правила. Несмотря на то, что системы, основанные на правилах, имеют долгую историю использования в Искусственном Интеллекте (ИИ), в таких системах отсутствует механизм для борьбы с нечеткими последствиями и нечеткими антекедентами. В нечеткой логике этот механизм обеспечивается исчислением нечетких правил. Исчисление нечетких правил служит базисом для того, что можно назвать Нечеткой Зависимостью и Командным Языком (FDCL). Несмотря на то, что FDCL не используется явно в тулбоксе, он фактически является одним из его основных компонентов. В большинстве применений нечеткой логики нечеткое логическое решение является, в действительности, переводом человеческого решения в FDCL.
Тренд, которая растет в видимости, связан с использованием нечеткой логики в сочетании с нейрокомпьютерными и генетическими алгоритмами. В более общем случае нечеткая логика, нейровычисление и генетические алгоритмы могут рассматриваться как основные составляющие того, что можно назвать мягкими вычислениями. В отличие от традиционных, жестких вычислений, мягкие вычисления учитывают неточность реального мира. Руководящий принцип мягких вычислений: Используйте допуск к неточности, неопределенности и частичной истинности, чтобы достичь прослеживаемости, робастности и низкой стоимости решения. В будущем мягкие вычисления могут играть все более важную роль в концепции и проекте систем, чей MIQ (Machine IQ) намного выше, чем у систем, разработанных обычными методами.
Среди различных комбинаций методологий в мягких вычислениях, та, которая имеет самую высокую видимость на этом этапе, - это нечеткая логика и нейровычисление, ведущая к нейро-нечетким системам. В рамках нечеткой логики такие системы играют особенно важную роль в индукции правил из наблюдений. Эффективный метод, разработанный доктором Роджером Джаном для этой цели, называется ANFIS (Адаптивная Нейро-Нечеткая Система Вывода). Этот метод является важным компонентом тулбокса.
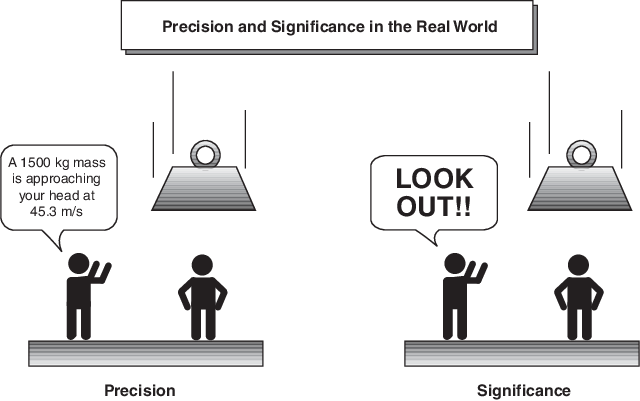
Нечеткая логика аппроксимирует человеческое мышление и хорошо справляется с балансом компромисса между точностью и значимостью. Например, предупреждая кого-то о падающем к ним объекте, быть точным о точной массе и скорости не обязательно.
Нечеткая логика является удобным способом сопоставить входное пространство с выходом пространством. Рассмотрим следующие примеры.
С информацией о том, насколько хорошим был ваш сервис в ресторане, нечеткая логическая система может сказать вам, каковы должны быть советы.
С вашей спецификацией того, как жарко вы хотите воды, нечеткая логическая система может настроить клапан крана в правильном направлении.
С информацией о том, как далеко находится тема вашей фотографии, нечеткая логическая система может фокусировать линзу для вас.
С информацией о том, как быстро машина движется и как тяжело работает двигатель, нечеткая логическая система может переключать передачи для вас.
Нечеткая система ведет себя как черный ящик, который преобразует входное пространство в выход пространство. Для примера можно сопоставить входное пространство всех возможных рейтингов ресторана со всеми возможными значениями совета.
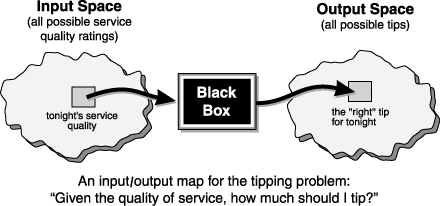
Определение соответствующего количества советов требует отображения входов с соответствующими выходами. Между входом и выходом предыдущий рисунок показывает черный ящик, который может содержать любое количество вещей: нечеткие системы, линейные системы, экспертные системы, нейронные сети, дифференциальные уравнения, интерполированные многомерные интерполяционные таблицы или даже духовный консультант, просто чтобы назвать несколько возможные опции. Очевидно, что список может продолжаться и дальше.
Из десятков способов заставить черный ящик работать, оказывается, что нечеткий часто является очень лучшим способом. Почему это должно быть? Как однажды заметил Лотфи Заде, которого принято считать отцом нечеткой логики, «Практически в каждом случае можно создавать один и тот же продукт без нечеткой логики, но нечеткий быстрее и дешевле».
Вот список общих наблюдений о нечеткой логике:
Нечеткую логику концептуально легко понять.
Математические концепции, лежащие в основе нечетких рассуждений, очень просты. Нечеткая логика является более интуитивно понятным подходом без далеко идущей сложности.
Нечеткая логика гибка.
С любой заданной системой легко наслаивать больше функциональности, не начиная снова с нуля.
Нечеткая логика толерантна к неточным данным.
Все неточно, если присмотреться достаточно внимательно, но больше того, большинство вещей неточны даже при тщательном осмотре. Нечеткие рассуждения строят это понимание в процессе, а не привязывают его к концу.
Нечеткая логика может моделировать нелинейные функции произвольной сложности.
Можно создать нечеткую систему, которая будет соответствовать любому набору входно-выходных данных. Этот процесс особенно прост с помощью адаптивных методов, таких как Adaptive Neuro-Fuzzy Inference Systems (ANFIS), которые доступны в программном обеспечении Fuzzy Logic Toolbox.
Нечеткая логика может быть построена на верхнюю часть опыта экспертов.
В прямом отличие от нейронных сетей, которые берут обучающие данные и генерируют непрозрачные, непроницаемые модели, нечеткая логика позволяет полагаться на опыт людей, которые уже понимают вашу систему.
Нечеткая логика может быть смешана с обычными методами управления.
Нечеткие системы не обязательно заменяют обычные методы управления. Во многих случаях нечеткие системы увеличивают их и упрощают их реализацию.
Нечеткая логика основана на естественном языке.
Базис нечеткой логики является базисом для человеческого общения. Это наблюдение лежит в основе многих других операторов о нечеткой логике. Поскольку нечеткая логика построена на структурах качественного описания, используемых в повседневном языке, нечеткая логика проста в использовании.
Последний оператор, пожалуй, самое важное и заслуживает большего обсуждения. Естественный язык, который используется обычными людьми на ежедневном базисный, сформирован тысячами лет человеческой истории, чтобы быть удобным и эффективным. Предложения, написанные на обычном языке, представляют собой торжество эффективной коммуникации.
Нечеткая логика не является лекарством. Когда не следует использовать нечеткую логику? Самый безопасный оператор является первым, сделанным в этом введении: нечеткая логика является удобным способом сопоставить входное пространство с выходом пространством. Если вам это не удобно, попробуйте что-нибудь еще. Если более простое решение уже существует, используйте его. Нечеткая логика - это кодификация здравого смысла - используйте здравый смысл, когда реализуете его и, вероятно, примите верное решение. Многие контроллеры, например, отлично справляются, не используя нечеткую логику. Однако, если вы найдете время, чтобы ознакомиться с нечеткой логикой, вы увидите, что она может быть очень мощным инструментом для быстрой и эффективной работы с неточностью и нелинейностью.
Используя программное обеспечение Fuzzy Logic Toolbox, можно:
Создайте и отредактируйте системы нечеткого вывода с помощью функций командной строки или Fuzzy Logic Designer приложения.
Автоматически генерируйте нечеткие системы с помощью кластеризации или адаптивных нейро-нечетких методов.
Автоматическая настройка параметров нечеткой логической системы с помощью методов оптимизации, таких как генетические алгоритмы и оптимизация роя частиц. Для получения дополнительной информации см. Раздел «Настройка систем нечеткого вывода».
Симулируйте свою нечеткую систему в Simulink® моделируйте с помощью блока Fuzzy Logic Controller.
Автоматически сгенерируйте код для оценки систем нечеткого вывода. Для получения дополнительной информации смотрите Развертывание систем нечеткого вывода.