surrogateopt Алгоритмsurrogateopt Обзор алгоритмаАлгоритм суррогатной оптимизации чередуется между двумя фазами.
Создайте суррогат - создайте options.MinSurrogatePoints случайные точки в границах. Оцените (дорогую) целевую функцию в этих точках. Создайте суррогат целевой функции путем интерполяции функции радиального базиса через эти точки.
Поиск Минимума - Поиск минимума целевой функции путем выборки нескольких тысяч случайных точек в границах. Оцените функцию заслуг на основе суррогатного значения в этих точках и на расстояниях между ними и точками, где (дорогая) целевая функция была оценена. Выберите лучшую точку в качестве кандидата, как измерено функцией заслуг. Оцените целевую функцию в самой лучшей точке кандидата. Эта точка называется adaptive point. Обновите суррогат, используя это значение, и повторите поиск.
Во время фазы Конструкции Surrogate алгоритм создает точки выборки из квазирандомной последовательности. Построение интерполирующей функции радиального базиса занимает по крайней мере nvars + 1 точка выборки, где nvars - количество переменных задачи. Значение по умолчанию options.MinSurrogatePoints является 2*nvars или 20, в зависимости от того, какая из них больше.
Алгоритм останавливает фазу Поиска Минимума, когда все точки поиска слишком близки (меньше опции MinSampleDistance) к точкам, где целевая функция была ранее оценена. Смотрите Поиск для получения минимальной информации. Этот переключатель из фазы поиска минимума называется surrogate reset.
В описании алгоритма суррогатной оптимизации используются следующие определения.
Ток - точка, где целевая функция была оценена совсем недавно.
Действующий - точка с наименьшим значением целевой функции среди всех, оцененных с момента последнего суррогатного сброса.
Лучший - точка с наименьшим значением целевой функции среди всех, оцененных до сих пор.
Начальная - точки, если таковые имеются, которые вы передаете решателю в InitialPoints опция.
Случайные точки - Точки в суррогатной фазе конструкции, где решатель оценивает целевую функцию. Обычно решатель берёт эти точки из квазирандомной последовательности, масштабированной и сдвинутой, чтобы остаться в границах. Квазирандомная последовательность подобна псевдослучайной последовательности, такой как rand возвращает, но находится с более равномерными интервалами. См. https://en.wikipedia.org/wiki/Low-discrepancy_sequence. Однако, когда количество переменных выше 500, решатель берёт точки из последовательности латинских гиперкубов. См. https://en.wikipedia.org/wiki/Latin_hypercube_sampling.
Адаптивные точки - Точки в фазе поиска минимума, где решатель оценивает целевую функцию.
Функция заслуг - См. Определение функции заслуг.
Оцененные точки - Все точки, в которых известно значение целевой функции. Эти точки включают начальные точки, конструкции Surrogate и точки Search for Minimum, в которых решатель оценивает целевую функцию.
Точки выборки. Псевдослучайные точки, где решатель оценивает функцию заслуг во время фазы Поиска Минимума. Эти точки не являются точками, в которых решатель оценивает целевую функцию, за исключением случаев, описанных в Search for Minimum Details.
Чтобы создать суррогат, алгоритм выбирает квазирандомные точки в границах. Если вы передаете начальный набор точек в InitialPoints опция, алгоритм использует эти точки и новые квазирандомные точки (при необходимости), чтобы достичь общего числа options.MinSurrogatePoints.
Когда BatchUpdateInterval > 1, минимальное количество случайных точек выборки, используемых для создания суррогата, больше из MinSurrogatePoints и BatchUpdateInterval.
Примечание
Если некоторые верхние и нижние границы равны, surrogateopt удаляет эти «фиксированные» переменные из задачи перед созданием суррогата. surrogateopt плавно управляет переменными. Так, например, если вы проходите начальные точки, передайте полный набор, включая любые фиксированные переменные.
На последующих фазах Construct Surrogate алгоритм использует options.MinSurrogatePoints квазирандомные точки. Алгоритм оценивает целевую функцию в этих точках.
Алгоритм создает суррогат как интерполяцию целевой функции с помощью интерполятора радиального базиса (RBF). Интерполяция RBF имеет несколько удобных свойств, которые делают её подходящей для построения суррогата:
Интерполятор RBF определяется с помощью той же формулы в любом количестве измерений и с любыми числами точек.
Интерполятор RBF принимает предписанные значения в оцененных точках.
Оценка интерполятора RBF занимает мало времени.
Добавление точки к существующей интерполяции занимает относительно мало времени.
Построение RBF интерполятора включает решение N-на-N линейной системы уравнений, где N - количество суррогатных точек. Как показал Powell [1], эта система имеет уникальное решение для многих RBF.
surrogateopt использует кубический RBF с линейным хвостом. Этот RBF минимизирует меру бестиражности. См. Гутманн [4].
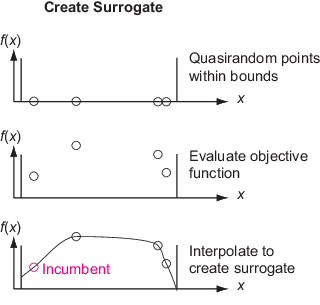
Алгоритм использует только начальные и случайные точки в первой фазе Construct Surrogate и использует только случайные точки в последующих фазах Construct Surrogate. В частности, алгоритм не использует никаких адаптивных точек из фазы Search for Minimum в этом суррогате.
Решатель ищет минимум целевой функции, следуя процедуре, которая связана с локальным поиском. Решатель инициализирует scale для поиска со значением 0.2. Шкала похожа на радиус области поиска или размер сетки в поиске шаблона. Решатель стартует с текущей точки, которая является точкой с наименьшим значением целевой функции с момента последнего суррогатного сброса. Решатель ищет минимум merit function, которая относится как к суррогату, так и к расстоянию от существующих точек поиска, чтобы попытаться сбалансировать минимизацию суррогата и поиск пространства. См. Определение функции заслуг.
Решатель добавляет сотни или тысячи псевдослучайных векторов с масштабированной длиной к действующей точке, чтобы получить sample points. Эти векторы имеют нормальные распределения, сдвинуты и масштабированы на границы в каждой размерности и умножены на шкалу. При необходимости решатель изменяет точки выборки так, чтобы они оставались в пределах границ. Решатель оценивает функцию заслуг в точки выборки, но не в любой точке options.MinSampleDistance предварительно рассчитанной точки. Точка с самым низким значением функции заслуг называется адаптивной точкой. Решатель оценивает значение целевой функции в адаптивной точке и обновляет суррогат этим значением. Если значение целевой функции в адаптивной точке достаточно ниже действующего значения, то решатель считает поиск успешным и устанавливает адаптивную точку в качестве действующего. В противном случае решатель считает поиск неудачным и не меняет действующего пользователя.
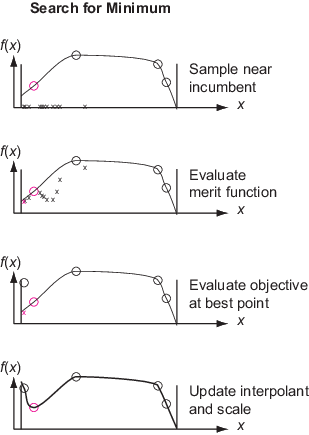
Решатель изменяет шкалу, когда достигается первое из этих условий:
С момента последнего изменения шкалы происходит три успешных поиска. В этом случае масштаб увеличивается вдвое, до максимальной длины шкалы 0.8 умножить размер прямоугольника, заданного границами.
max(5,nvar) неудачные поиски происходят с момента последнего изменения шкалы, где nvar - количество переменных задачи. В этом случае шкала уменьшается вдвое, до минимальной длины шкалы 1e-5 умножить размер прямоугольника, заданного границами.
Таким образом, случайный поиск в конечном счете концентрируется вблизи текущей точки, которая имеет маленькое значение целевой функции. Затем решатель геометрически уменьшает масштаб к минимальной длине шкалы.
Решатель не вычисляет функцию заслуг в точках внутри options.MinSampleDistance рассчитанной точки (см. Определения для суррогатной оптимизации). Решатель переключается с фазы Search for Minimum на фазу Construct Surrogate (другими словами, выполняет суррогатный сброс), когда все точки выборки находятся внутри MinSampleDistance рассчитанных точек. Обычно этот сброс происходит после того, как решатель уменьшает шкалу, так что все точки выборки плотно кластеризуются вокруг действующего участника.
Когда BatchUpdateInterval опция больше 1решатель генерирует BatchUpdateInterval адаптивные точки перед обновлением суррогатной модели или изменением действующего сотрудника. Обновление включает все адаптивные точки. Эффективно алгоритм не использует никакой новой информации, пока не сгенерирует BatchUpdateInterval адаптивные точки, а затем алгоритм использует всю информацию для обновления суррогата.
Функция заслуг f заслугах (x) является взвешенной комбинацией двух членов:
Масштабированный суррогат. Задайте s мин как минимальное суррогатное значение среди выборочных точек, s макс как максимальное, и s (x) как суррогатное значение в x точки. Тогда масштабированный суррогатный S (x)
s (x) неотрицательна и равна нулю в точках x, которые имеют минимальное суррогатное значение среди точек выборки.
Масштабированное расстояние. Задайте xj, j = 1,..., k как k оцененные точки. Задайте dij как расстояние от точки выборки i до вычисленных k точки. Установите d min = min (dij) и d max = max (dij), где минимум и максимум взяты по всем i и j. Масштабированное D расстояния (x) является
где d (x) - минимальное расстояние между точкой x и вычисленной точкой. D (x) неотрицательна и равна нулю в точках x, которые максимально далеки от оцененных точек. Таким образом, минимизация D (x) приводит алгоритм к точкам, которые далеки от оцененных точек.
Функция заслуг является выпуклой комбинацией масштабируемого суррогата и масштабируемого расстояния. Для весовой w с 0 < w < 1, функция заслуг является
Большое значение w придает значение суррогатным значениям, заставляя поиск минимизировать суррогат. Небольшое значение w придает значение точкам, которые далеки от оцененных точек, ведя поиск к новым областям. Во время фазы поиска минимума вес w переходит через эти четыре значения, как предложено Regis и Shoemaker [2]: 0,3, 0,5, 0,8 и 0,95.
surrogateopt Алгоритмsurrogateopt ОбзорКогда некоторые или все переменные целые числа, как указано в intcon аргумент, surrogateopt изменяет некоторые аспекты алгоритма последовательного surrogateopt. Это описание посвящено главным образом изменениям, а не всему алгоритму.
При необходимости, surrogateopt перемещает указанные ограничения для intcon точки так, чтобы они были целыми числами. Также, surrogateopt гарантирует, что заданная начальная точка является целочисленной допустимой и допустимой относительно границ. Затем алгоритм генерирует квазирандомные точки как в нецелочисленном алгоритме, округляя целочисленные точки до целочисленных значений. Алгоритм генерирует суррогат в точности как в нецелочисленном алгоритме.
Поиск минимума выполняется с использованием той же функции заслуг и последовательности весов, что и прежде. Самое различие, что surrogateopt использует три различных метода дискретизации случайных точек, чтобы найти минимум функции вознаграждения. surrogateopt выбирает дискретизатор в цикле, сопоставленном с весами, согласно следующей таблице.
Цикл дискретизатора
| Вес | 0.3 | 0.5 | 0.8 | 0.95 |
| Образец | Случайный | Случайный | OrthoMADS | GPS |
Шкала - Каждый дискретизатор отбирает точки в масштабируемой области вокруг действующего лица. Целочисленные точки имеют шкалу, которая начинается в ½ раз с ширины границ и корректируется точно так же, как нецелочисленные точки, за исключением того, что ширина увеличивается до 1, если бы она когда-либо опускалась ниже 1. Шкала непрерывных точек развивается в точности как в нецелочисленном алгоритме.
Случайный - Дискретизатор генерирует целое число точки равномерно случайным образом в пределах шкалы, с центром у действующего сотрудника. Дискретизатор генерирует непрерывные точки согласно Гауссову со средним нулем от действующего лица. Ширина выборок целочисленных точек умножается на шкалу, как и стандартное отклонение непрерывных точек.
OrthoMADS - семплер выбирает ортогональную систему координат равномерно случайным образом. Алгоритм затем создает точки выборки вокруг действующего сотрудника, добавляя и вычитая текущую шкалу раз каждый единичный вектор в системе координат. Алгоритм округляет целочисленные точки. Это создает 2N выборки (если только некоторые целочисленные точки не округлены до действующего президента), где N - количество проблемных размерностей. OrthoMADS также использует на две точки больше, чем 2N фиксированных направлений, одна в [+ 1, + 1,..., + 1], а другая в [-1, -1,..., -1], для общего числа 2N + 2 точек. Затем дискретизатор неоднократно пополняет 2N + 2 шага, создавая более мелкий и мелкий набор точек вокруг действующего президента, округляя при этом целочисленные точки. Этот процесс заканчивается, когда либо достаточно образцов, либо округление не вызывает новых выборок.
GPS - семплер похож на OrthoMADS, кроме того, что вместо выбора случайного набора направлений, GPS использует невращенную систему координат.
После дискретизации сотен или тысяч значений функции заслуг, surrogateopt обычно выбирает минимальную точку и оценивает целевую функцию. Однако при двух обстоятельствах, surrogateopt выполняет другой поиск под названием Поиск по дереву перед оценкой цели:
С момента последнего поиска дерева было 2N шагов, называемых Case A.
surrogateopt собирается выполнить суррогатный сброс, называемый Case B.
Поиск по дереву выполняется следующим образом, подобно процедуре в intlinprog, как описано в ветвь и Bound. Алгоритм делает дерево, находя целое число и создавая новую задачу, которая имеет привязку к этому значению либо на один выше, либо на один ниже, и решая подпрограмму с этой новой привязкой. После решения подпроблемы алгоритм выбирает другое целое число, которое будет ограничено или выше, или ниже единицей.
Случай A: Используйте масштабированный радиус выборки в качестве общих границ и выполняйте до 1000 шагов поиска.
Случай B: Используйте исходные границы задачи как общие границы и выполняйте до 5000 шагов поиска.
В этом случае решение подпрограммы означает выполнение fmincon
'sqp' алгоритм от непрерывных переменных, начиная с действующего с заданными целыми значениями, поэтому поиск локального минимума функции заслуг.
Поиск по дереву может занять много времени. Так surrogateopt имеет внутренний предел времени, чтобы избежать чрезмерного времени на этом шаге, ограничивая как количество шагов случая A, так и случая B.
В конце поиска Tree алгоритм принимает лучшее из точки, найденной Tree Search, и точки, найденной предыдущим поиском минимума, как измерено функцией заслуг. Алгоритм оценивает целевую функцию в этой точке. Остальная часть целочисленного алгоритма в точности совпадает с непрерывным алгоритмом.
Когда задача имеет линейные ограничения, алгоритм изменяет свою процедуру поиска таким образом, чтобы сохранить все точки допустимыми относительно этих ограничений и относительно границ при каждой итерации. На фазах конструкции и поиска алгоритм создает только линейно допустимые точки с помощью процедуры, подобной patternsearch
'GSSPositiveBasis2N' алгоритм опроса.
Когда задача имеет целочисленные ограничения и линейные ограничения, алгоритм сначала создает линейно допустимые точки. Затем алгоритм пытается удовлетворить целочисленным ограничениям процессом округления линейно допустимых точек к целым числам с помощью эвристика, который пытается сохранить точки линейно допустимыми. Когда этот процесс неудачен в получении достаточно допустимых точек для построения суррогата, алгоритм вызывает intlinprog попытаться найти больше точек, которые допустимы относительно границ, линейных ограничений и целочисленных ограничений.
surrogateopt Алгоритм с нелинейными ограничениямиКогда задача имеет нелинейные ограничения, surrogateopt изменяет ранее описанный алгоритм несколькими способами.
Первоначально и после каждого суррогатного сброса алгоритм создает суррогаты целевой и нелинейной функций ограничения. Впоследствии алгоритм отличается в зависимости от того, обнаружила ли фаза Construct Surrogate какие-либо допустимые точки; нахождение допустимой точки эквивалентно допустимости существующей точки при построении суррогата.
Действующий сотрудник недопустим - Этот случай, называемый Фаза 1, включает поиск допустимой точки. В фазе поиска минимума перед встречей с допустимой точкой, surrogateopt изменяет определение функции заслуг. Алгоритм подсчитывает количество ограничений, которые нарушаются в каждой точке, и рассматривает только те точки с наименьшим количеством нарушенных ограничений. Среди этих точек алгоритм выбирает точку, которая минимизирует максимальное нарушение ограничений как лучшую (функция наименьших заслуг) точку. Это лучшая точка для действующего президента. Впоследствии, пока алгоритм не встретит допустимую точку, он использует эту модификацию функции заслуг. Когда surrogateopt оценивает точку и находит, что это допустимо, допустимая точка становится действующей, и алгоритм находится в Фазе 2.
Действующее лицо допустимо - Этот случай, называемый Фаза 2, протекает так же, как и стандартный алгоритм. Алгоритм игнорирует недопустимые точки с целью вычисления функции заслуг.
Алгоритм протекает согласно Mixed-Integer surrogateopt Algorithm со следующими изменениями. После каждого 2*nvars точки, где алгоритм оценивает целевые и нелинейные функции ограничений, surrogateopt вызывает fmincon функция для минимизации суррогата, удовлетворяющая суррогатным нелинейным ограничениям и границам, где границы масштабируются текущим масштабным коэффициентом. (Если действующий сотрудник недопустим, fmincon игнорирует цель и пытается найти точку, удовлетворяющую ограничениям.) Если задача имеет как целое, так и нелинейные ограничения, то surrogateopt вызывает поиск дерева вместо fmincon.
Если задача является задачей выполнимости, что означает, что она не имеет целевой функции, то surrogateopt выполняет суррогатный сброс сразу после того, как находит допустимую точку.
surrogateopt АлгоритмПараллельный surrogateopt алгоритм отличается от последовательного алгоритма следующим образом:
Параллельный алгоритм поддерживает очередь точек, на которых можно вычислить целевую функцию. Эта очередь на 30% больше, чем количество параллельных рабочих процессов, округленных. Очередь больше, чем количество работников, чтобы минимизировать вероятность простоя работника, потому что нет точки для оценки.
Планировщик берет точки из очереди в FIFO моде и присваивает их работникам, когда они становятся простаивающими, асинхронно.
Когда алгоритм переключается между фазами (Search for Minimum и Construct Surrogate), существующие оцениваемые точки остаются в обслуживании, и любые другие точки в очереди сбрасываются (отбрасываются из очереди). Таким образом, обычно количество случайных точек, которые алгоритм создает для суррогатной фазы Конструкции, самое большее options.MinSurrogatePoints + PoolSize, где PoolSize количество параллельных рабочих. Точно так же после суррогатного сброса алгоритм все еще имеет PoolSize - 1 адаптивные точки, которые оценивают его работники.
Примечание
В настоящее время параллельная суррогатная оптимизация не обязательно дает воспроизводимые результаты, из-за непродуктивности параллельной синхронизации, которая может привести к различным путям выполнения.
surrogateopt АлгоритмКогда выполняйте параллельно по смешано-целочисленной задаче, surrogateopt выполняет процедуру поиска дерева на узле, а не на параллельных работниках. Используя новейший суррогат, surrogateopt ищет меньшее значение суррогата после того, как каждый работник вернется с адаптивной точкой.
Если целевая функция не является дорогостоящей (длительное время), то эта процедура поиска по дереву может оказаться узким местом на хосте. Напротив, если целевая функция является дорогой, то процедура поиска по дереву занимает небольшую часть общего вычислительного времени и не является узким местом.
[1] Пауэлл, М. Дж. Д. Теория радиального базиса Приближения функций в 1990 году. In Light, W. A. (editor), Advances in Numerical Analysis, Volume 2: Wavelets, Subdivision Algorithms и Radial Basis Functions. Clarendon Press, 1992, pp. 105-210.
[2] Реджис, Р. Г., и К. А. Шумейкер. Стохастический метод радиального базиса для глобальной оптимизации дорогих функций. ИНФОРМС Ж. Вычисления 19, 2007, с. 497-509.
[3] Wang, Y., and C. A. Shoemaker. Общая среда стохастического алгоритма для минимизации дорогих объективных функций черного ящика на основе суррогатных моделей и анализа чувствительности. arXiv:1410.6271v1 (2014). Доступно в https://arxiv.org/pdf/1410.6271.
[4] Гутманн, Г.-М. Метод радиальной функции базиса для глобальной оптимизации. Журнал глобальной оптимизации 19, март 2001, стр. 201-227.