Что такое мультиобъективная оптимизация?

Вы, возможно, должны будете сформулировать проблемы с более чем одной целью, поскольку одна цель с несколькими ограничениями может неадекватно представлять проблему, с которой сталкиваются. Если это так, существует вектор целей,

F (<reservedrangesplaceholder7>) = [<reservedrangesplaceholder6> 1 (<reservedrangesplaceholder5>), <reservedrangesplaceholder4> 2 (<reservedrangesplaceholder3>)..., <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>)],

(1)

это должно быть каким-то образом реализовано. Относительная важность этих целей в целом не известна до тех пор, пока не будут определены наилучшие возможности системы и не будут достигнуты компромиссы между целями, которые полностью понимаются. По мере увеличения числа целей компромиссы, вероятно, станут комплексными и менее легко поддаются количественной оценке. Дизайнер должен полагаться на свою интуицию и способность выражать настройки в течение всего цикла оптимизации. Таким образом, требования к стратегии мультиобъективного проекта должны позволить выразить естественную формулировку задачи и иметь возможность решить проблему и ввести настройки в численно отслеживаемую и реалистичный проект задачу.

Мультиобъективная оптимизация связана с минимизацией вектора целей F (x), которые могут быть предметом ряда ограничений или границ:

$\begin{array}{l} \min_{x \in ℝ^{n}} F (x), при условии , что \\ G_{i} (x) = 0, i = 1, ..., k_{e}; G_{i} (x) \leq 0, i = k_{e} + 1, ..., k; l \leq x \leq u . \end{array}$

Обратите внимание, что поскольку F (x) является вектором, если какой-либо из компонентов F (x) конкурирует, уникального решения этой задачи нет. Вместо этого для характеристики целей должна использоваться концепция нефинфериальности в Zadeh [4] (также названная оптимальностью Парето в Censor [1] и Da Cunha и Polak [2]). Неинфекционное решение является решением, в котором улучшение одной цели требует деградации другой. Чтобы более точно определить эту концепцию, рассмотрим допустимую область, в параметр пространства. x является элементом n -мерных вещественных чисел $x \in ℝ^{n}$ который удовлетворяет всем ограничениям, то есть,

$Ω = {x \in ℝ^{n}},$

при условии, что

$\begin{array}{l} G_{i} (x) = 0, i = 1, ..., k_{e}, \\ G_{i} (x) \leq 0, i = k_{e} + 1, ..., k, \\ l \leq x \leq u . \end{array}$

Это позволяет определить соответствующую допустимую область для пространства целевых функций

$Λ = {y \in ℝ^{m} : y = F (x), x \in Ω} .$

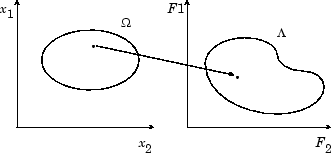
Вектор эффективности F (x) преобразует пространство параметров в пространство целевых функций, как представлено в две размерностей на рисунке 9-1, Отображая Пространство параметров в Пространство целевых функций.

Рисунок 9-1, Преобразование пространства параметров в пространство целевых функций

Теперь можно задать неинференциальную точку решения.

Определение: Точка $x * \in Ω$ является неинференциальным решением, если для некоторой окрестности x * не существует x, такого что $(x * + Δ x) \in Ω$ и

$\begin{array}{l} F_{i} (x * + Δ x) \leq F_{i} (x *), i = 1, ..., m, и \\ F_{j} (x * + Δ x) < F_{j} (x *) по крайней мере , для одного j . \end{array}$

В двумерном представлении рисунка 9-2 «Набор неинференциальных решений», набор неинференциальных решений лежит на кривой между C и D. Точки A и B представляют специфические неинференциальные точки.

Рисунок 9-2, Набор неинфекционных решений

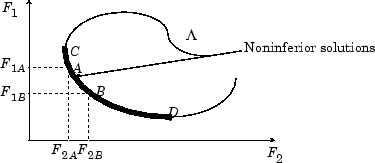
A и B - явно ненизшие точки решения, потому что улучшение одной цели, <reservedrangesplaceholder9> 1, требует деградации в другой цели_, <reservedrangesplaceholder8> 2, то есть, <reservedrangesplaceholder7> 1 <reservedrangesplaceholder6> <<reservedrangesplaceholder5> 1 <reservedrangesplaceholder4>, <reservedrangesplaceholder3> 2 <reservedrangesplaceholder2>> <reservedrangesplaceholder1> 2 <reservedrangesplaceholder0>.

Поскольку любая точка, которая является нижней точкой, представляет собой точку, в которой улучшение может быть достигнуто во всех целях, ясно, что такая точка не имеет значения. Мультиобъективная оптимизация, следовательно, связана с генерацией и выбором неинфекционных точек решения.

Неинфериорные решения также называются Pareto optima. Общей целью в мультиобъективной оптимизации является построение оптимума Парето.

Документация Global Optimization Toolbox

Поддержка

Памятка переводчика

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Документация