Этот пример показывает, как найти набор Парето для двухцелевой функции двух переменных. В примере представлены два подхода к минимизации: использование задачи Optimize Live Editor и работа в командной строке.
Двухцелевая функция f (x), где x также двумерна, является
Создайте новый live скрипт, нажав кнопку New Live Script в разделе File на вкладке Home.
Вставьте задачу Optimize Live Editor. Щелкните вкладку Insert, а затем в разделе Code выберите Task > Optimize.
Для использования при вводе данных о задаче вставьте новый раздел, нажав кнопку Section Break на вкладке Insert. Новые разделы появляются выше и ниже задачи.
В новом разделе над задачей введите следующий код, чтобы определить количество переменных и нижнюю и верхнюю границы.
nvar = 2; lb = [0 -5]; ub = [5 0];
Чтобы поместить эти переменные в рабочую область, запустите раздел, нажав Ctrl+Enter.
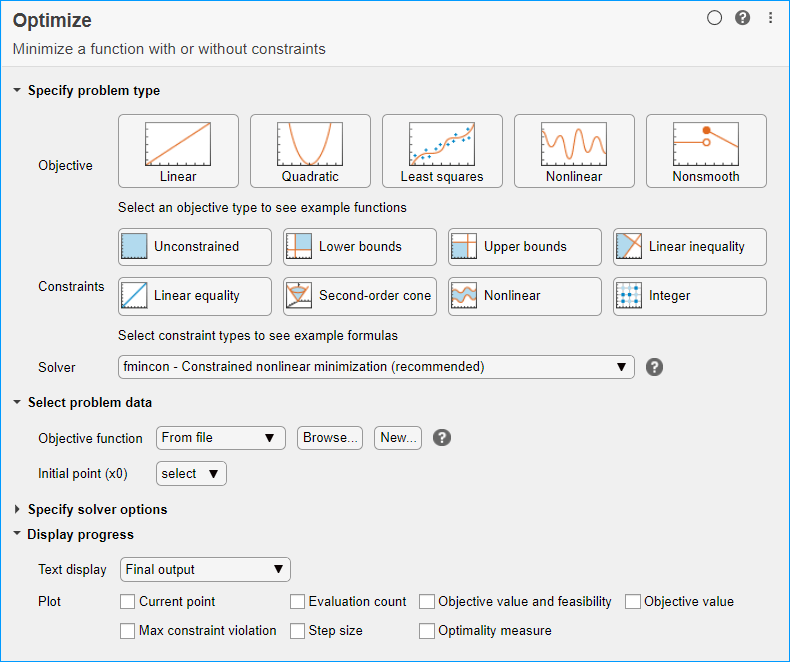
Задайте тип задачи
В Specify problem type разделе задачи нажмите кнопку Objective > Nonlinear.
Нажмите кнопки Constraints > Lower bounds и Upper bounds.
Выберите Solver > gamultiobj - Multiobjective optimization using genetic algorithm.
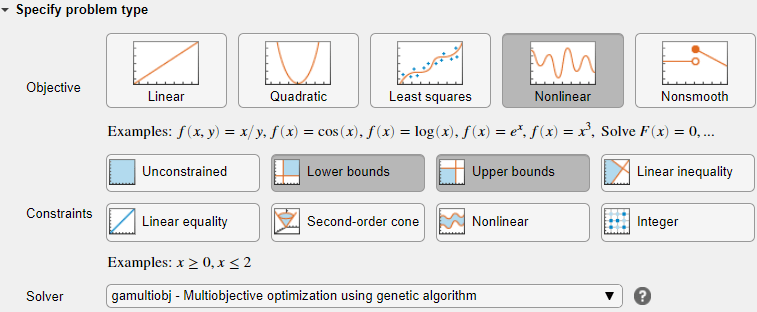
Выберите данные задачи
В разделе Select problem data выберите Objective function > Local function и нажмите кнопку New. Функция появится в новом разделе под задачей.
Отредактируйте полученное определение функции, чтобы оно содержало следующий код.
function f = mymulti1(x) f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2; f(1) = f(2) - 10*x(1)^2; end
В Select problem data разделе выберите функцию Local function > mymulti1.
Выберите Number of variables > nvar.
Выберите Lower bounds > From workspace > lb и Upper bounds > From workspace > ub.
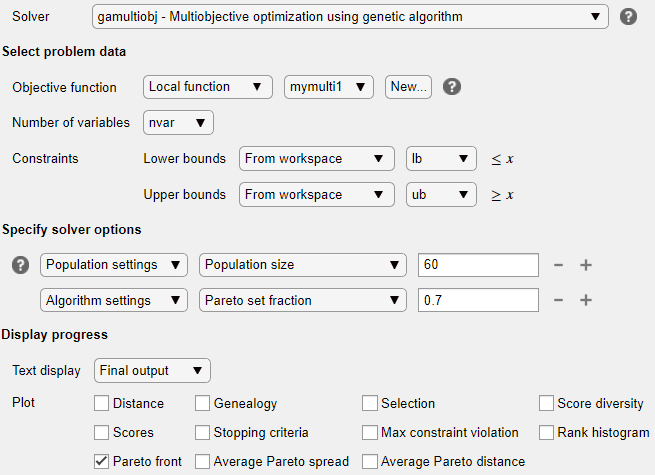
Задайте опции решателя
Разверните раздел Specify solver options задачи и нажмите кнопку Add. Чтобы иметь более плотный, более связный фронт Парето, задайте большие, чем по умолчанию, населения, выбирая Population settings > Population size > 60.
Чтобы иметь больше населения на фронте Парето, чем настройки по умолчанию, нажмите кнопку +. В полученных опциях выберите Algorithm > Pareto set fraction > 0.7.
Задание параметров отображения
В Display progress разделе задачи выберите Pareto front функции построения графика.
Запустите решатель и исследуйте результаты
Чтобы запустить решатель, нажмите кнопку options ⁝ в верхней части окна задачи и выберите Run Section. График появляется в отдельном окне рисунка и в области выхода задачи.
![Set of points on a convex curve from about [-38,33] to about [-5,0]](multiobj_plot2.png)
График показывает компромисс между двумя компонентами f, который построен в пространстве целевых функций. Для получения дополнительной информации смотрите рисунок 9-2, Набор неинференциальных решений.
Чтобы выполнить ту же оптимизацию в командной строке, выполните следующие шаги.
Создайте mymulti1 файл функции на MATLAB® путь.
function f = mymulti1(x) f(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - (x(1)*x(2))^2; f(1) = f(2) - 10*x(1)^2; end
Установите опции и границы.
options = optimoptions('gamultiobj','PopulationSize',60,... 'ParetoFraction',0.7,'PlotFcn',@gaplotpareto); lb = [0 -5]; ub = [5 0];
Запустите оптимизацию, используя опции.
[solution,ObjectiveValue] = gamultiobj(@mymulti1,2,...
[],[],[],[],lb,ub,options);И задача Optimize Live Editor, и командная строка позволяют вам сформулировать и решить задачи, и они дают одинаковые результаты. Командная строка более упорядочена, но предоставляет меньше помощи для выбора решателя, настройки задачи и выбора опций, таких как функции построения графика. Можно также начать задачу с помощью Optimize, а затем сгенерировать код для использования в командной строке, как в Решать Ограниченную Нелинейную Задачу, Основанную на Решателе.
Вы можете просмотреть эту проблему другими способами. Следующий рисунок содержит график кривых уровня двух целевых функций, границы Парето, вычисленные gamultiobj (коробки) и значения x истинной границы Парето (алмазы, соединенные почти прямой линией). Истинные пограничные точки Парето находятся там, где кривые уровня целевых функций параллельны. Алгоритм вычисляет эти точки, находя, где градиенты целевых функций параллельны. Рисунок построен в пространстве параметров; см. фигуру 9-1, «Отображение пространства параметров в пространство целевых функций».
Контуры целевых функций и граница Парето
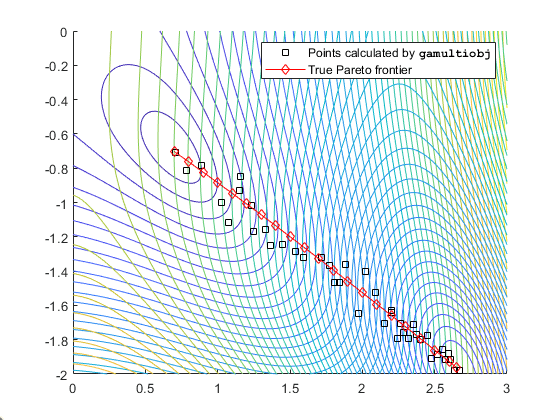
gamultiobj находит концы сегмента линии, что означает, что он находит полную протяженность границы Парето.