Вы идентифицируете модель, чтобы можно было точно вычислить динамическую систему ответ на вход. Существует два способа сгенерировать идентифицированный ответ модели:
Simulation вычисляет ответ модели с помощью входных данных и начальных условий.
Prediction вычисляет ответ модели в некотором заданном количестве времени в будущем, используя текущие и прошлые значения измеренных входных и выходных значений, а также начальные условия.

В системе идентификации цель состоит в том, чтобы создать реалистичную динамическую систему, которая может затем использоваться или передаваться для цели приложения. В этом контексте основными ролями симуляции и предсказания в System Identification Toolbox™ являются предоставление инструментов для идентификации модели, а также для выбора, настройки и валидации этих моделей.
Вы можете:
Идентифицируйте свою модель таким образом, чтобы минимизировать либо предсказание (prediction focus), либо ошибку симуляции (simulation focus)
Визуализируйте ответ модели по сравнению с другими моделями и с измерениями данных
Проверьте свою модель путем сравнения ее отклика с измеренными входными/выходными данными, которые не использовались для исходной оценки модели
Ваш выбор подхода к симуляции или предсказанию зависит от потребностей вашего приложения, а также от того, где вы находитесь в рабочем процессе системы идентификации:
Когда вы идентифицируете свои модели, одношаговое особое внимание предсказания обычно даёт лучшие результаты. Это преимущество связано с тем, что при использовании как входных, так и выходных измерений одношаговое предсказание учитывает природу нарушений порядка. Учет нарушений порядка обеспечивает наиболее статистически оптимальные результаты.
Когда вы проверяете свои модели, симуляция обычно обеспечивает более проницательный подход для оценки того, как ваша модель будет работать в широкой области значений условий. Однако ваше приложение также может управлять валидацией на основе прогнозов. Для примера, если вы планируете использовать свою модель для проектирования системы управления, можно подтвердить модель, предсказав ее реакцию на временной горизонт, который представляет доминирующие временные константы модели.
Можно работать или во временном интервале, или в частотном диапазоне, и оставаться сопоставимым с областью входных/выходных данных. Для данных частотного диапазона результаты симуляции являются продуктами преобразования Фурье входной и частотной функции модели. Поскольку идентификация модели частотной характеристики игнорирует динамику шума, особое внимание симуляции и одноэтапное особое внимание предсказания дают ту же идентифицированную модель. Для валидации в частотный диапазон используйте симуляцию.
Для примеров смотрите:
Вы можете получить более подробное понимание различий между симуляцией и предсказанием, применив эти методы к простой системе первого порядка.
Simulation означает вычисление отклика модели с помощью входных данных и начальных условий. Временные выборки отклика модели совпадают со временными выборками входных данных, используемых для симуляции. Другими словами, заданные входы u (t 1,..., tN), симуляция генерирует y (t 1,..., tN). Следующая схема иллюстрирует этот процесс.

Для системы в непрерывном времени симуляция означает решение дифференциального уравнения. Для системы в дискретном времени симуляция означает непосредственное применение уравнений модели.
Для примера рассмотрим динамическую модель, описанную разностным уравнением первого порядка, которое использует шаг расчета 1 секунду:
y (t +1) = <reservedrangesplaceholder5> <reservedrangesplaceholder4> (<reservedrangesplaceholder3>) + <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>),
где y - выход, а u - вход.
Эта система эквивалентна следующему блоку.
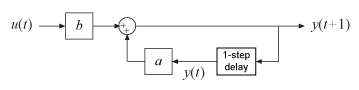
Предположим, что идентификация вашей модели предоставляет вам предполагаемые значения параметров a = 0,9 и b = 1,5. Тогда уравнение становится:
y (t +1) = 0.9 y (<reservedrangesplaceholder2>) + 1.5 u (<reservedrangesplaceholder0>).
Теперь предположим, что вы хотите вычислить значения y (1), y (2), y (3),... для заданных входных значений u (0) = 2, u (1) = 1, u (2) = 4,... Здесь y (1) является значением выхода в первый момент дискретизации. Используя начальное условие y (0) = 0, значения y (t) для раз t = 1, 2 и 3 могут быть вычислены как:
y (1) = 0.9 y (0) + 1.5 u (0) = (0.9) (0) + (1.5) (2) = 3
y (2) = 0.9 y (1) + 1.5 u (1) = (0.9) (3) + (1.5) (1) = 4.2
y (3) = 0.9 y (2) + 1.5 u (2) = (0.9) (4.2) + (1.5) (4) = 9.78
Prediction означает проецирование отклика модели k шаги вперед в будущее с помощью текущих и прошлых значений измеренных входных и выходных значений. k называется prediction horizon и соответствует предсказанию выхода в момент времени k Ts, где Ts является шагом расчета. Другими словами, учитывая измеренные входы um (t 1..., <reservedrangesplaceholder8> <reservedrangesplaceholder7> + k) и измеряемые выходы ym (t 1..., <reservedrangesplaceholder3> <reservedrangesplaceholder2>), предсказание производит yp (<reservedrangesplaceholder0>).
Например, предположим, что вы используете датчики для измерения um входного сигнала (t) и ym выходного сигнала (t) физической системы, описанной в предыдущем уравнении первого порядка. Уравнение становится:
yp (t +1) = <reservedrangesplaceholder5> <reservedrangesplaceholder4> (<reservedrangesplaceholder3>) + <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>),
где y - выход, а u - вход.
Версия предиктора предыдущего блока симуляции:
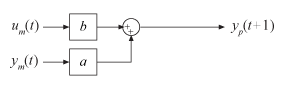
В 10-й момент дискретизации (t = 10) измеренный выход ym (10) равен 16 мм, а соответствующий входной um (10) равен 12 Н. Теперь вы хотите предсказать значение выходного сигнала в будущее время t = 11. Используя предыдущее уравнение, предсказанная выходная yp является:
yp (11) = 0.9 ym (10) + 1.5 um (10)
Следовательно, предсказанное значение будущего выходного y (11) во время t = 10 равняется :
yp (11) = 0.9*16 + 1.5*12 = 32.4
В целом, чтобы предсказать реакцию модели k шаги в будущее (k ≥ 1) от текущей временной t, вы должны знать входы до времени t + k и выходы до временного t:
yp (t + k) = f (um (t + k), um (t + <reservedrangesplaceholder5>–1)..., um (<reservedrangesplaceholder3>), um (t –1)..., um (0),
ym (<reservedrangesplaceholder5>) , ym (t –1), ym (t –2)..., ym (0))
um (0) и ym (0) являются начальными состояниями. f() представляет predictor, которая является динамической моделью, форма которой зависит от структуры модели.

Предсказатель «один шаг вперед» от предыдущего примера, yp модели y (<reservedrangesplaceholder6>) + <reservedrangesplaceholder5> <reservedrangesplaceholder4> (t-1) = <reservedrangesplaceholder2> <reservedrangesplaceholder1> (<reservedrangesplaceholder0>):
yp (t +1) = – <reservedrangesplaceholder5> <reservedrangesplaceholder4> (<reservedrangesplaceholder3>) + <reservedrangesplaceholder2> <reservedrangesplaceholder1> (t +1)
В этом случае простого одношагового предиктора самое новое предсказание основано только на измерениях. Для многоэтапных предикторов динамическая модель распространяет состояния внутри страны, используя предыдущие предсказанные состояния в дополнение к входам. Поэтому каждый предсказанный выход возникает из комбинации измеренных входных и выходных параметров и предыдущих предсказанных выходов.
Можно задать k любое положительное целое значение до количества измеренных выборок данных. Если вы устанавливаете k на ∞, то никакие предыдущие выходы не используются в расчете прогноза, и предсказание возвращает тот же результат, что и симуляцию. Если вы задаете k целое число, больше, чем количество выборок данных, predict устанавливает k на Inf и выдает предупреждение. Если ваш намерение состоит в том, чтобы выполнить предсказание за время области значений превышающее последний момент измеренных данных, используйте forecast.
Для примера, показывающего предсказание и симуляцию в MATLAB®, см. Сравнение предсказанного и симулированного отклика идентифицированной модели с измеренными данными.
Не все модели поддерживают прогнозирующий подход. Для предыдущей динамической модели, структура поддерживает использование прошлых данных. Эта поддержка не существует в моделях структуры Output-Error (OE) (H (z) = 1). В прошлых выходах нет информации, которая может использоваться для прогнозирования будущих выходных значений. В этих случаях предсказание и симуляция совпадают. Даже модели, которые обычно используют прошлую информацию, могут все еще иметь структуру OE в особых случаях. Модели в пространстве состояний (idss) иметь структуру OE, когда K=0. Полиномиальные модели (idpoly) также иметь структуру OE, когда a=c=d=1. В этих особых случаях предсказание и симуляция эквивалентны, и модель возмущения фиксируется на 1.
Этот пример показывает, как визуализировать как предсказанный ответ модели, так и моделируемый ответ модели идентифицированной линейной модели.
Идентифицируйте модель пространства состояний третьего порядка, используя входные/выходные измерения в z1.
load iddata1 z1; sys = ssest(z1,3);
sys - идентифицированное в непрерывном времени пространство состояний (idss) модель. Здесь, sys идентифицируется с использованием по умолчанию 1-шагового особого внимания предсказания, который минимизирует 1-шаговую ошибку предсказания. Это особое внимание обычно обеспечивает лучшую общую модель.
Теперь используйте compare для построения графика предсказанной характеристики. В данном примере задайте горизонт предсказания kstep до 10 шагов и использование compare для построения графика предсказанной характеристики относительно исходных данных измерений. Эта настройка kstep указывает, что каждая точка отклика в будущем составляет 10 шагов относительно данных измерений, используемых для предсказания этой точки.
kstep = 10; figure compare(z1,sys,kstep)

На этом графике каждая точка данных представляет предсказанный выход, сопоставленный с выходными данными измерения, который был сделан, по меньшей мере, на 10 шагов раньше. Например, точка на t = 15 секундах основана на измерениях, проведенных на t = 5 секундах или ранее.
График иллюстрирует различия между откликом модели и исходными данными. Процент в легенде является значением соответствия NRMSE. Он представляет, насколько близок выход предсказанной модели к данным.
Чтобы улучшить свои результаты, можно уменьшить горизонт предсказания.
kstep = 5; figure compare(z1,sys,kstep)

Значение соответствия NRMSE улучшилось по сравнению со значением соответствия, полученным в 10-ступенчатом случае. В фактическом приложении существуют различные факторы, которые влияют на то, насколько малым может быть горизонт предсказания. К ним относятся временные константы и требования к интерполяциям приложений.
Можно просмотреть симулированный отклик для сравнения, а не предсказанный ответ, используя kstep по умолчанию для compare, что Inf. При симуляции в расчете отклика используются только входные данные, а не измеренные выходные данные.
figure compare(z1,sys)

Моделируемые и 10-ступенчатые предсказанные отклики дают одинаковые общие проценты подгонки.
Чтобы изменить параметры отображения на графике, щелкните правой кнопкой мыши график, чтобы получить доступ к контекстному меню. Для примера, чтобы построить график ошибки между предсказанным выходом и измеренным выходом, выберите Error Plot в контекстном меню.
Этот пример показов, как идентифицировать модели с предсказанием особого внимания и с особым вниманием симуляции. Сравните ответы моделей прогнозирования-фокуса и фокуса симуляции с исходными данными оценки и с данными валидации, которые не использовались для оценки.
Когда вы идентифицируете модель, алгоритм использует 'Focus' опция, чтобы определить, минимизировать ли ошибку предсказания или ошибку симуляции. Значение по умолчанию является 'prediction'. Вы можете изменить это, изменив 'Focus' опция для 'simulation'.
Загрузите данные измерения z1, и разделите его на две половины z1e и z1v. Одна половина используется для идентификации модели, а другая - для валидации модели.
load iddata1 z1; %z1e = z1(1:150); %To avoid ordqz stall %z1v = z1(151:300); z1e = z1(1:155); z1v = z1(156:300);
Идентифицируйте модель пространства состояний третьего порядка sys_pf использование входных/выходных измерений в z1e. Используйте опцию по умолчанию 'Focus' для этой модели, которая является 'предсказанием'.
sys_pf = ssest(z1e,3);
sys_pf - идентифицированное в непрерывном времени пространство состояний (idss) модель.
Используя тот же набор данных измерений, идентифицируйте вторую модель пространства состояний sys_sf который устанавливает 'Focus' на 'simulation'.
opt = ssestOptions('Focus','simulation'); sys_sf = ssest(z1e,3,opt);
Используйте compare функция для симуляции реакции на обе идентифицированные модели.
figure compare(z1e,sys_pf,sys_sf)

Модель, идентифицированная с прогнозирующим особым вниманием, имеет более высокое значение подгонки NRMSE, чем модель, идентифицированная с особым вниманием симуляции.
Теперь выполните сравнение с данными валидации. Это сравнение показывает, насколько хорошо модель работает с условиями, которые не были частью ее идентификации.
figure compare(z1v,sys_pf,sys_sf)

Значения подгонки для обеих моделей улучшаются. Однако модель с предсказанием особого внимания остается выше модели с особым вниманием симуляции.
compare | forecast | predict | sim