Когда вы моделируете динамическую систему, которая не начинается с отдыха, вы должны инициализировать эту симуляцию, чтобы соответствовать начальным условиям. Для примера вы можете сравнивать симулированный отклик с измеренными данными или с предыдущей симуляцией или расчетом. Можно хотеть начать симуляцию в установившемся условии или продолжить симуляцию из предыдущего симуляции.
System Identification Toolbox™ предоставляет несколько методов для определения начальных условий (IC) для использования. Эти методы включают использование:
Моделируйте результаты идентификации
Текущие или прошедшие измерения входных/выходных данных
Информация о состоянии из предыдущих симуляций
В следующей таблице результирующие подходы доступны и когда их использовать. Для краткости в этой таблице используется термин « симуляция» в широком смысле для обозначения «симуляция или предсказание». Для получения дополнительной информации смотрите Моделирование и Предсказание Идентифицированного Выхода Модели.
Подходы к оценке начальных условий
| Когда использовать | Подход | Сводные данные по методам |
|---|---|---|
Вы симулируете idss, idtf, idproc, idpoly, или idgrey моделируйте ответ с помощью тех же входных данных, с которыми вы идентифицировали свою модель. | Извлечение IC из результатов идентификации модели (возвращенные значения или отчет об оценке). Оценка возвращает информацию IC в одной из следующих форм.
|
Примеры: Решите различия в значениях подгонки между идентификацией модели и командой сравнения Применение начальных условий при симуляции идентифицированных линейных моделей |
Вы хотите воспроизвести результаты, сгенерированные compare (или сгенерирован графиком Model Output в приложении). | Использовать возвращенные ИС из |
Примеры: Совпадайте с Выходом сравнения Командного и нелинейного ARX Блока Model Применение начальных условий при симуляции идентифицированных линейных моделей |
| Вы симулируете ответ модели на заданный входной сигнал и хотите начать симуляцию в точке, которая приводит к ближайшему соответствию к заданному выходному сигналу. | Использовать Использовать Если исходная модель является |
Примеры: Применение начальных условий при симуляции идентифицированных линейных моделей Оценка начальных условий для линейной модели с использованием измеренных данных |
| Вы продолжаете симуляцию, например, для онлайн-обработки. Вы используете разделенный набор данных, например, для nlarx модель, когда findstates слишком дорого в вычислительном отношении. | data2state
Если исходная модель является idtf, idproc, или idpoly, сначала преобразуйте в форму пространства состояний, используя idss. Вы также можете использовать data2state неявно путем определения ваших прошлых данных в качестве прокси для начальных условий при использовании sim или predict с любой динамической моделью.Для получения дополнительной информации смотрите Оценка начальных условий из измеренных данных. | sys_ss = idss(sys)x0 = data2state(sys,z_p)или IO = struct или opt = predictOptions ('InitialCondition',IO). примеры: Оценка начальных условий для нелинейной модели ARX, Осмыслите использование исторических данных для симуляции модели |
| Вы работаете с продолжающимся моделированием и хотите основать начальные условия для текущего сегмента симуляции на предыдущем сегменте. Вы намерены начать свою основную симуляцию в устойчивом состоянии, и вы хотите иметь приквел, который имитирует запуск до устойчивого состояния от отдыха. | Используйте информацию о состоянии из предыдущего моделирования или предварительной симуляции. Если исходная модель является idtf, idproc, или idpoly, сначала преобразуйте в форму пространства состояний, используя idss. Для получения дополнительной информации смотрите Использование начальных условий из информации о прошлом состоянии. | sys_ss = idss(sys)x0 = x(end) от [y,y_sd,x] = sim(sys_ss,z_p)Пример: Продолжите симуляцию идентифицированной модели с использованием прошлых состояний |
В предыдущей таблице предлагаются различные методы оценки начальных условий. В следующих разделах эти методы суммируются источником данных оценки.
Оцените начальные условия из данных измерения, из которых вы получаете входы симуляции. Методы включают следующее.
Извлеките начальные условия из результатов идентификации модели, таких как отчет об идентификации для вашей модели или как возвращенные значения из compare. X0 представляет вектор начального состояния, а IC представляет initialCondition объект. Для примеров смотрите Разрешение Различий Значений Подгонки между Идентификацией Модели и Сравнение Команды, Сопоставление Выхода Сравнения Команды и Нелинейного Блока Model ARX и Применение Начальных Условий при Симуляции Идентифицированных Линейных Моделей.
Оцените начальные условия с помощью измеренных входных/выходных данных, используя функцию findstates для оценки начальных состояний, согласующихся с набором данных. Для получения примера смотрите Оценку начальных условий для линейной модели с использованием измеренных Данных.
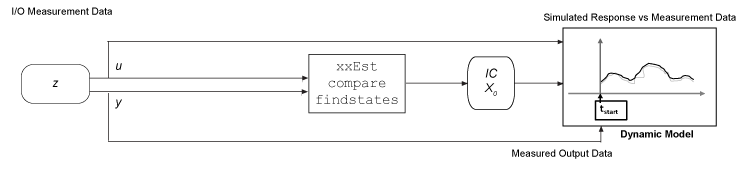
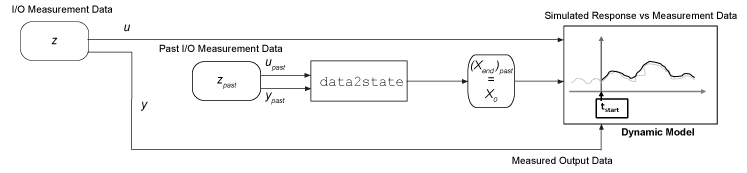
Оцените начальные условия из данных измерения, непосредственно предшествующих началу симуляции. Методы включают следующее.
Использование функции data2state для оценки конечного состояния набора данных. Прошлое конечное состояние затем становится начальным состоянием для последующей симуляции. Для получения примера смотрите Оценку начальных условий для нелинейной модели ARX.
Использование ваших прошлых данных в качестве прокси для начальных условий при использовании sim или predict. Когда вы запускаете симуляцию, модель внутренне вызывает data2state для тебя. Для получения примера смотрите Понимание использования исторических данных для симуляции модели.
Разделение используемого набора данных на две части. Сделать первую часть достаточно большой, чтобы позволить data2state для вычисления точного конечного состояния. Этот подход с разделением данных может быть намного менее интенсивным в вычислительном отношении, чем использование findstates на полном наборе данных, особенно для нелинейных моделей ARX. Для получения примера смотрите Оценку начальных условий для нелинейной модели ARX.
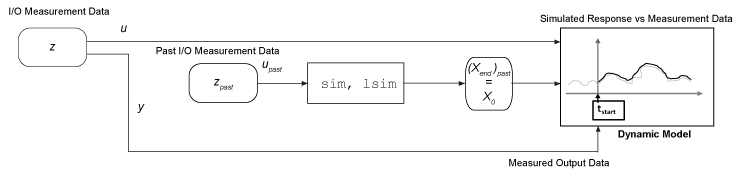
Используйте информацию о состоянии из предыдущих симуляций или предварительных симуляций. Если никакая предыдущая симуляция не доступна, можно выполнить предварительное моделирование от покоя или известного начального условия до точки начала симуляции. Конечные состояния прошлого или предварительной симуляции являются начальными состояниями для симуляции, которую вы хотите выполнить. Для получения примера смотрите Продолжить симуляцию идентифицированной модели с использованием прошлых состояний.
findstates и data2state функции являются наиболее общими инструментами для определения начального или конечного состояний из любых измерений входных/выходных данных. Однако, чтобы использовать эти функции, вы должны иметь структуру модели, которая включает явное представление состояния. Линейные модели кроме idss и idgrey не использовать явные состояния. Чтобы найти эквивалентные начальные состояния, можно преобразовать эти модели в idss Моделями и найдите начальные состояния из idss версии. Как альтернатива findstates, вы также можете использовать compare получить начальные условия без преобразования ваших моделей в форму пространство состояний. Для этих моделей, compare возвращает initialCondition объект, который содержит информацию о свободной реакции модели, в форме пространства состояний и соответствующих начальных состояниях.
После того, как вы оцените начальные условия, можно включить их в синтаксис симуляции командной строки, ваш Simulink® модель, или System Identification приложение.
Следующие примеры иллюстрируют оценку начальных условий для линейных моделей. Первый пример использует findstates и compare. Во втором и третьем примерах используются исторические данные. То есть примеры определяют начальные условия из данных, непосредственно предшествующих времени начала симуляции.
Используйте различные методы, чтобы получить начальные условия для линейной модели и сравнить результаты.
Оцените передаточную функцию для измеренных данных. Верните начальные условия в ic.
load iddata1 z1; [sys,ic] = tfest(z1,3); ic
ic =
initialCondition with properties:
A: [3x3 double]
X0: [3x1 double]
C: [0.2303 5.9117 2.2283]
Ts: 0
ic.X0
ans = 3×1
-1.7569
2.6195
-6.5177
sys является идентифицированной передаточной функцией в непрерывном времени (idtf) модель. ic является initialCondition объект. Система координат initialCondition объект представляет свободную реакцию системы в форме пространства состояний. Объект включает преобразованную A и C матрицы пространства состояний, которые соответствуют sys и предполагаемый вектор начального состояния X0.
Можно также использовать findstates найти начальные условия для линейных моделей, но только если они в idss или idgrey форма.
Преобразование sys в форму пространства состояний.
sys_ss = idss(sys);
Использование findstates для оценки начальных состояний.
X0 = findstates(sys_ss,z1)
X0 = 3×1
-1.7569
2.6195
-6.5177
Теперь используйте compare для оценки начальных состояний, используя исходную модель передаточной функции.
[y_tf,fit,ic2] = compare(z1,sys); ic2
ic2 =
initialCondition with properties:
A: [3x3 double]
X0: [3x1 double]
C: [0.2303 5.9117 2.2283]
Ts: 0
ic2.X0
ans = 3×1
-1.7569
2.6195
-6.5177
Векторы начального состояния идентичны во всех трех случаях.
Используйте исторические данные ввода-вывода в качестве прокси для начальных условий при симуляции модели. Вы сначала симулируете, используя sim и задайте исторические данные используя simOptions набор опций. Затем вы воспроизводите моделируемый выход путем преобразования исторических данных в начальные состояния вручную.
Загрузите набор данных с двумя входами и одним выходом.
load iddata7 z7
Идентифицируйте модель пространства состояний пятого порядка с помощью данных.
sys = n4sid(z7,5);
Разделите набор данных на две части.
zA = z7(1:15); zB = z7(16:end);
Симулируйте модель с помощью входного сигнала в zB.
uSim = zB;
Симуляция требует начальных условий. The значений сигналов in zA являются ли историческими данными, то есть они являются входными и выходными значениями за время, непосредственно предшествующее данным в zB. Использование zA в качестве прокси для необходимых начальных условий.
IO = struct('Input',zA.InputData,'Output',zA.OutputData); opt = simOptions('InitialCondition',IO);
Симулируйте модель.
ysim = sim(sys,uSim,opt);
Теперь воспроизведите выход, вручную сопоставив исторические данные с начальными состояниями sys. Для этого используйте data2state команда.
xf = data2state(sys,zA);
xf содержит значения состояний sys в то время сразу после последней выборки данных в zA.
Симулируйте систему с помощью xf как начальные состояния.
opt2 = simOptions('InitialCondition',xf);
ysim2 = sim(sys,uSim,opt2);Постройте график выхода sim командная ysim и результаты, вычисленные вручную ysim2.
plot(ysim,'b',ysim2,'--r')

ysim2 то же, что и ysim.
Оцените начальные условия для сегмента симуляции идентифицированной модели с помощью конечных состояний предыдущего сегмента симуляции.
Загрузите данные z1, который является iddata объект, содержащий входные и выходные данные. Оцените линейную модель пятого порядка из данных.
load iddata1 z1 plot(z1)

sys = n4sid(z1,5);
Разделите данные на два сегмента. Один сегмент z1past представляет данные для прошлой симуляции и начинается с рест. второго сегмента z1next представляет данные для последующей симуляции.
z1past = z1(1:150); z1next = z1(150:300);
Симулируйте ответ на входные данные в z1next без определения начальных условий.
ynext_no_ic = sim(z1next,sys);
plot(ynext_no_ic,z1next)
legend
title('Simulation Continuation Without Setting ICs')
Теперь определите конечные состояния, x0, для ответа на z1past входной .
[ypast,y_sd,xpast] = sim(z1past,sys); x0 = xpast(end,:)';
Используйте конечные состояния, чтобы задать начальные состояния для последующего ответа на z1next.
opt = simOptions('InitialCondition',x0); ynext_ic = sim(z1next,sys,opt); figure plot(ynext_ic,z1next) legend title('Simulation Continuation with Sychronized ICs')

Когда вы симулируете модель Гаммерштейна-Винера или нелинейную модель серого ящика и хотите использовать начальные условия, сопоставимые с набором данных измерений z, использование findstates.
Сравните моделируемый выход блока Hammerstein-Wiener Model с измеренным выходом системы. Вы улучшаете согласие между измеренным и моделируемым откликами путем оценки начальных значений состояния.
Загрузите выборочные данные.
load twotankdata
Создайте iddata объект из выборочных данных. Задайте 'Tstart' 0 так, чтобы время запуска данных совпадало со временем запуска Simulink 0f 0 с.
z1 = iddata(y,u,0.2,'Tstart',0,'Name','Two tank system');
Оцените модель Гаммерштейна-Винера с помощью данных.
mw1 = nlhw(z1,[1 5 3],pwlinear,pwlinear);
Теперь можно симулировать выход предполагаемой модели в Simulink, используя входные данные в z1. Для этого откройте предварительно сконфигурированную модель Simulink.
model = 'ex_idnlhw_block';
open_system(model);

Модель использует блоки Iddata Source, Hammerstein-Wiener и Scope. Следующие параметры блоков были предварительно сконфигурированы, чтобы указать данные оценки, оценочную модель и начальные условия:
Параметры блоков Исходного блока Iddata:
Объект IDDATA - z1
Параметры блоков блока Hammerstein-Wiener Model:
Модель - mw1
Начальные условия - Zero (по умолчанию)
Запустите симуляцию.
Просмотрите различие между измеренным выходом и выходом модели при помощи блока Scope.
simOut = sim(model);
open_system([model '/Scope'])

Чтобы улучшить согласие между измеренным и моделируемым откликами, оцените вектор начального состояния для модели из данных оценки z1, использование findstates. Задайте максимальное количество итераций для оценки как 100. Задайте горизонт предсказания следующим Inf, так что алгоритм вычисляет начальные состояния, которые минимизируют ошибку симуляции.
opt = findstatesOptions; opt.SearchOptions.MaxIterations = 100; x0 = findstates(mw1,z1,Inf,opt);
Установите значение параметров блоков Initial conditions блока Hammerstein-Wiener Model равным State Values. Начальными состояниями по умолчанию являются x0.
set_param([model '/Hammerstein-Wiener Model'],'IC','State values');
Еще раз запустите симуляцию и посмотрите различие между измеренным выходом и выходом модели в блоке Scope. Теперь различие между измеренной и симулированными откликами уменьшена.
simOut = sim(model);

Когда вы симулируете нелинейную модель ARX и хотите использовать начальные условия, сопоставимые с набором данных измерений z, у вас есть выбор, какой подход взять.
Вы можете использовать findstates. Однако для нелинейных моделей ARX этот подход имеет стоимость вычислительных затрат, если набор данных велик.
X0 = findstates(m,z,Inf);
Можно разбить набор данных на два фрагментов. Используйте первую nx выборки входных/выходных данных как прошлых данных, где nx - самая большая задержка регрессора в модели. Затем используйте data2state для вычисления конечного состояния «прошлых данных». Затем вы сможете симулировать модель для остальных nx+1:end входные данные с любым выбранным подходом симуляции. Оба compare и приложение System Identification автоматически использует этот подход для нелинейных моделей ARX.
nx = max(getDelayInfo(m)); % Find the largest regressor delay
past_data = z1(1:nx);
X0 = data2state(mw1,z1(1:nx));Следующий пример иллюстрирует использование метода разделения данных для нелинейной модели ARX.
Используйте два различных метода для оценки начальных условий для нелинейной модели ARX. Симулируйте каждый вместе с данными измерений и сравните с симуляцией, которая инициализируется в покое.
Загрузите входные/выходные данные z и постройте его. Используйте первые 1000 точек z для оценки нелинейной модели ARX.
load twotankdata z = iddata(y,u,0.2); z1 = z(1:1000); plot(z1) title('Estimation data')

mdlnlarx = nlarx(z1,[5 1 3],wavenet);
Извлеките первые 250 точек z1 (50 секунд) как z1sim для симуляции сравнения. Моделируйте mdlarx не устанавливая начальных условий и строя график отклика вместе с измеренным выходом в z1sim.
z1sim = z1(1:250); data_no_ic = sim(mdlnlarx,z1sim); plot(data_no_ic,z1sim) title('Nonlinear ARX Model with No Initial Condition Setting') grid on legend('location','se')

Использование findstates для оценки начальных условий. В порядок минимизации ошибки симуляции задайте Inf для горизонта предсказания. Затем установите sim опция для InitialCondition на findstates результаты. Постройте график отклика рядом с измеренным выходом.
x0fs = findstates(mdlnlarx,z1sim,Inf); opt = simOptions('InitialCondition',x0fs); data_fs = sim(mdlnlarx,z1sim,opt); figure plot(data_fs,z1sim) title('Nonlinear ARX Model with IC Estimation Using findstates') grid on legend('location','se')

Реакция и измеренный выход теперь начинаются примерно с одной и той же точки.
Теперь используйте data2states способ оценки начальных условий. Сначала разбейте набор данных на два фрагментов. Используйте первую nx выборки z1sim как «прошлые данные», где nx - самая большая задержка регрессора в модели.
nx = max(getDelayInfo(mdlnlarx))
nx = 5
z1past = z1sim(1:nx); z1sim2 = z1sim(nx+1:end);
Использование data2state для вычисления конечного состояния «прошлых данных». Симулируйте ответ с помощью входов, начиная с z1sim(nx+1). Постройте график отклика вместе с полным z1sim данные измерений так, чтобы можно было сравнить с findstates график.
x0d2s = data2state(mdlnlarx,z1past); opt = simOptions('InitialCondition',x0d2s); data_d2s = sim(mdlnlarx,z1sim2,opt); figure plot(data_d2s,z1sim) title('Nonlinear ARX Model with IC Estimation Using data2state') grid on legend('location','se')

Если вы выполняли каждый раздел отдельно, можно обнаружить, что data2states метод завершен быстрее, чем findstates способ.
Теперь сравните ответы для всех трех случаев начальных условий.
plot(data_fs,data_d2s,data_no_ic) title('Nonlinear ARX model Responses for Three IC Approaches Compared') legend('location','se')

Ответы для случаев, использующих findstates и data2state практически одинаковые. Ответ для случая, когда начальные условия не были установлены, сходится в конечном счете, но только через 30 секунд.
compare | compareOptions | data2state | findstates | predict | predictOptions | sim | simOptions