Оптимизация нелинейных функций

Минимизация функций одной переменной

Учитывая математическую функцию одной переменной, можно использовать fminbnd функция для поиска локального минимизатора функции в заданном интервале. Для примера рассмотрим humps.m функция, которая обеспечивается MATLAB ®. Следующий рисунок показывает график humps.

x = -1:.01:2;
y = humps(x);
plot(x,y)
xlabel('x')
ylabel('humps(x)')
grid on

Figure contains an axes. The axes contains an object of type line.

Чтобы найти минимум humps функция в области значений (0.3,1), использование

x = fminbnd(@humps,0.3,1)

x = 0.6370

Подробную информацию о процессе решения можно узнать при помощи optimset чтобы создать опции со Display значение опции установлено в 'iter'. Передайте получившиеся опции, чтобы fminbnd.

options = optimset('Display','iter');
x = fminbnd(@humps,0.3,1,options)

 
 Func-count     x          f(x)         Procedure
    1       0.567376      12.9098        initial
    2       0.732624      13.7746        golden
    3       0.465248      25.1714        golden
    4       0.644416      11.2693        parabolic
    5         0.6413      11.2583        parabolic
    6       0.637618      11.2529        parabolic
    7       0.636985      11.2528        parabolic
    8       0.637019      11.2528        parabolic
    9       0.637052      11.2528        parabolic
 
Optimization terminated:
 the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04

x = 0.6370

Итеративное отображение показывает текущее значение x и значение функции в f(x) каждый раз, когда выполняется вычисление функции. Для fminbndодно вычисление функции соответствует одной итерации алгоритма. В последнем столбце показана процедура fminbnd использует в каждой итерации поиск золотого сечения или параболическую интерполяцию. Для получения дополнительной информации смотрите Итеративное отображение решателя оптимизации.

Минимизация функций нескольких переменных

fminsearch функция подобна fminbnd кроме того, что он обрабатывает функции многих переменных. Задайте стартовый вектор x0, а не начальный интервал. fminsearch пытается вернуть вектор x, который является локальным минимизатором математической функции около этого стартового вектора.

Чтобы попробовать fminsearch, создайте функцию three_var из трех переменных, x, y, и z.

function b = three_var(v)
x = v(1);
y = v(2);
z = v(3);
b = x.^2 + 2.5*sin(y) - z^2*x^2*y^2;

Теперь найдите минимум для этой функции, используя x = -0.6, y = -1.2, и z = 0.135 в качестве начальных значений.

v = [-0.6,-1.2,0.135];
a = fminsearch(@three_var,v)

a =
    0.0000   -1.5708    0.1803

Максимизация функций

fminbnd и fminsearch решатели пытаются минимизировать целевую функцию. Если у вас есть задача максимизации, то есть задача формы

$\max_{x} f (x),$

затем задайте g (x ) = - f (x), и минимизируйте g.

Для примера, чтобы найти максимум tan (cos (x)) около x = 5, оцените:

[x fval] = fminbnd(@(x)-tan(cos(x)),3,8)

x =
    6.2832

fval =
   -1.5574

Максимальный - 1.5574 (отрицательный из сообщенных fval), и происходит при x = 6,2832. Этот ответ верен, так как, до пяти цифр, максимум является tan (1 ) = 1,5574, что происходит в x = 2 π = 6,2832.

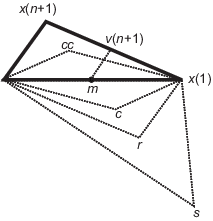
`fminsearch` Алгоритм

fminsearch использует алгоритм симплекса Нелдера-Мида, как описано в Lagarias et al. [1]. Этот алгоритм использует симплекс n + 1 точек для n -мерных векторов x. Алгоритм сначала делает симплекс вокруг начального предположения _x 0, добавляя 5% каждого компонента x 0 (i) _к x 0. Алгоритм использует эти векторы n как элементы симплекса в сложение для x 0. (Алгоритм использует 0,00025 как компонент _i если x 0 (i) = 0.) Затем алгоритм неоднократно изменяет симплекс согласно следующей процедуре.

Примечание

Ключевые слова для fminsearch итеративное отображение появляется жирным шрифтом после описания шага.

Пусть x (i) обозначают список точек в текущем симплексе, i = 1,..., n + 1.
Упорядочьте точки в симплексе от самого низкого значения функции f (x (1)) до самого высокого f (x (n + 1)). На каждом шаге итерации алгоритм отбрасывает текущий x худшей точки (n + 1) и принимает другую точку в симплекс. [Или, в случае шага 7 ниже, он изменяет все точки n со значениями выше f (x (1))].
Сгенерируйте точку reflected
r = 2 m – x (n + 1), (1)
где
m = и x (i )/ n, i = 1... n, (2)
и вычислите f (r).
Если f (x (1)) ≤ <reservedrangesplaceholder5> (<reservedrangesplaceholder4>) <f (x (<reservedrangesplaceholder1>)), примите r и закончите эту итерацию. Размышлять
Если f (r) < f (x (1)), вычислите точку расширения s
s = m + 2 (m – x (n + 1)), (3)
и вычислите f (s).
1. Если f (s) < f (r), примите s и завершите итерацию. Расшириться
2. В противном случае примите r и завершите итерацию. Размышлять
Если f (r) ≥ f (x (n)), выполните contraction между m и x (n + 1) или r, в зависимости от того, которое имеет более низкое значение целевой функции.
1. Если f (r) < f (x (n + 1)) (то есть r лучше x (n + 1)), вычислите
  c = m + (r – m)/2 (4)
  и вычислите f (c). Если f ( c) < f (r), примите c и завершите итерацию. Контракт вне
  В противном случае перейдите к шагу 7 (усадка).
2. Если f (r) ≥ f (x (n + 1)), вычислите
  cc = m + (x (n + 1) – m)/2 (5)
  и вычислите f (cc). Если f ( cc) < f (x (n + 1)), примите cc и завершите итерацию. Контракт внутри
  В противном случае перейдите к шагу 7 (усадка).
Вычислим точки n
v (<reservedrangesplaceholder4>) = x (1) + (x (<reservedrangesplaceholder1>) – x (1))/2 (6)
и вычислите f (v (i)), i = 2,..., n + 1. Симплекс при следующей итерации - x (1), v (2),..., v (n + 1). Сжаться

Следующий рисунок показывает точки, которые fminsearch может вычислять в процедуре, вместе с каждым возможным новым симплексом. Исходный симплекс имеет жирный контур. Итерации продолжаются до тех пор, пока они не удовлетворяют критерию остановки.

Graphical representation of fminsearch algorithm showing reflection, expansion, contraction, and shrinking points.

Ссылка

[1] Лагария, Дж. К., Дж. А. Ридс, М. Х. Райт и П. Э. Райт. «Свойства сходимости метода Нелдера-Мида Симплекса в низких Размерностях». SIAM Journal of Optimization, Vol. 9, Number 1, 1998, pp. 112-147.

Документация